【GNN】NLNN：self-Attention 的泛化框架

2020 年 5 月 31 日 AINLP

今天学习的是 CMU 和 Facebook 的同学 2017 年的工作《Non-local Neural Networks》，发表于 CVPR 18，作者王小龙，导师是何凯明老师，这篇论文的截止目前的引用量有 1100 多次。

这篇论文的应用领域最初是在计算机视觉，作者提出的非局部神经网络（non-local neural network，NLNN）来捕获深度神经网络的长依赖关系，这种非局部运算是对所有位置特征的加权计算，因此也可以被看作是不同“self-attention”的方法的统一。

1.Introduction

卷积运算和递归运算是典型的局部运算（只考虑局部信息），长距离依赖关系通常是通过不断迭代来形成更大的感受野。但这种方式有很多缺点，包括计算效率低，优化困难等。

作者受 CV 领域中经典的非局部均值滤波的启发提出了 NLNN，将一个位置相应为所有位置特征的加权计算，这种位置位置可以是空间、时间或者时空，也就是说这种方法的应用领域适用于图像、序列和视频等问题。

这种非局部运算有几大优点：

与卷积运算和递归运算相比，非局部运算通过计算任意两个位置之间的交互直接捕获长依赖；
即使神经网络的层数不多也能达到最佳效果；
非局部运算支持可变的输入大小，并且可以轻松与其他运算（如卷积运算）相结合。

在介绍正文之前，先接单介绍下非局部均值法。

非局部均值滤波（Non-Local Means，NLM）是 Buades 等人 2005 年的论文《A non-local algorithm for image denoising》提出的一种对传统领域滤波方法进行改进的一种滤波方法，其考虑图像的自相似性，充分利用图像中的非局部信息来辅助滤波降噪。

算法的主要原理是计算图像中所有像素与当前像素的相似性，其公式定义为：

其中，为两个像素的相似性；表示以像素 i 为中心固定大小的领域；为灰度强度的映射向量；为归一化常数；为平滑参数。

2.NLNN

2.1 Formulation

首先我们先来看下非局部运算的通用公式，受非局部均值滤波方法的影响，我们有：

其中，表示 i 位置的特征向量；f 为计算相似性的函数；g 为将点映射为向量的映射函数（可以理解为计算点的特征）；为一个归一化因子。

非局部运算考虑的是所有位置，而局部运算如卷积操作只考虑节点的周围信息，递归运算只考虑上一步的信息。

非局部运算与全连接运算的区别主要有两点：

非局部运算的多输出值会受到输入值之间关系的影响（因为要计算），而全连接运算通过学习到权重来计算输入到输出的映射，所以不同位置的关系是不会影响到输出，一定程度上损失了位置的相关性；
非局部运算支持可变大小的输入，而全连接运算的输入大小是固定的；
非局部操作可以很容易地与卷积/递归层一起使用，而不像全连接层只能放到神经网络的最后使用。这便使得我们能够将非局部信息和局部信息结合起来，来构建一个更丰富的层次结构，

2.2 Instantiations

接下来我们介绍几种具体的例子。

由于作者在实验中发现不同形式的实例其实对结果的影响不太大（因为这种非局部的行为才是主要的影响因素），所以为了简化操作，只考虑线性映射函数，其中，是一个可学习的权重矩阵。

接下来我们考虑 f 的不通过中形式：

「Gaussian」：从非局部均值滤波和双边滤波的角度来看，显而易见的首先想到高斯滤波：

「Embedded Gaussian」：考虑到 Embedding 的向量空间，我们有高斯滤波的变种：

self-attention 其实就是 non-local 的 Embedded Gaussian 的一种特殊情况。对于所有 i，我们把变成计算所有 j 的 Softmax，得到：

这便是《Attention is all your need》中的表达式。

此时，作者便将 self-attention 与传统的非局部均值联系到了一起，并将基于序列的 self-attention 推广空间和时空领域中。

此外，与《Attention》那篇论文不同的是，作者发现 Attention 的形式对于研究 case 来说并不必须的，为了说明这点，作者有给出了以下几种表达形式。

「Dot product」：考虑点乘相似度：

N 为输入向量 x 的数量，而不是 f 的和，这样做的目的在于简化梯度的计算。

这个版本与 Embedded Gaussian 的区别在于是否做 softmax。

「Concatenationn」：考虑连接运算：

其中，为连接运算，为将 concat 向量转换成标量的权重向量。

当然，也可以是其他变种，这一定程度上也说明了 non-local 的灵活性。

2.3 Non-local Block

这一节作者将非局部运算变成一个非局部模块，以便插入到现有的神经网络结构中。

作者将其设计成残差模块，让其学习 x 的残差：

这种残差结构可以使得在任意的预训练模型中直接插入一个新的非局部模块而不用改变原有的网络结构。考虑计算量问题，在输入比较大的情况下可以只在高阶语义层中引入 non-local layer，此外也可以通过 pooling 层来减少计算量。

看一个简单的实现：

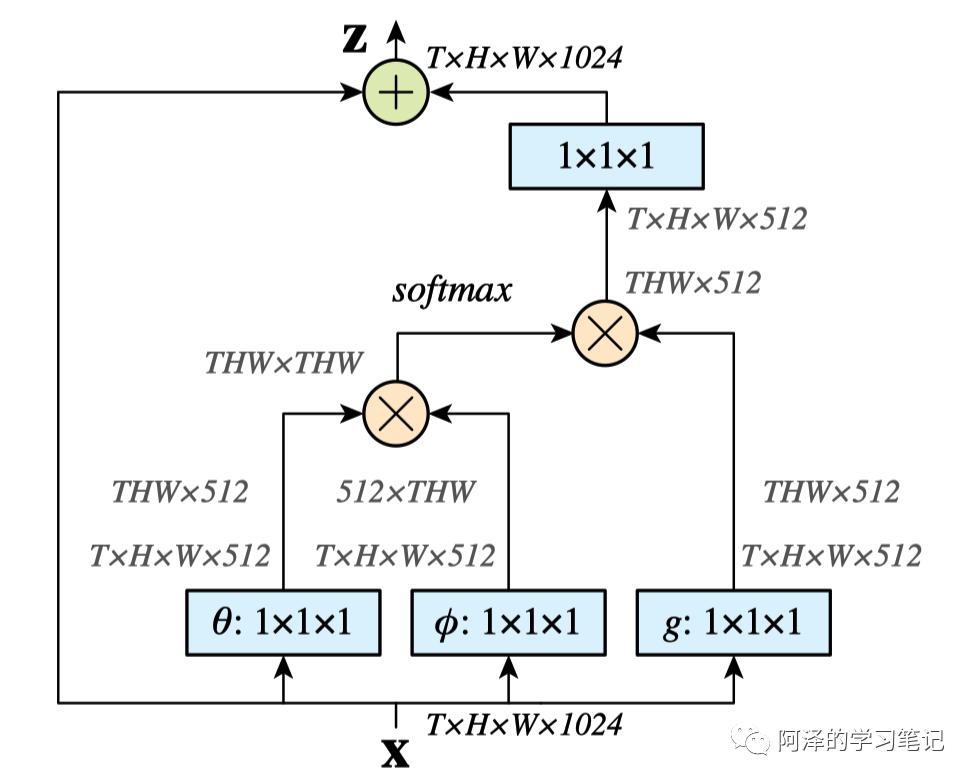
为元素点和，为矩阵相乘。

我们通过利用的卷积将的 channel 数量控制为 X 的一半，形成一个 bottleneck 的结构，可以大大减少计算量。在输出时利用可以将 channel 还原，从保证了输入输出的维度一致。

此外，还有一个下采样（subsampling）的 trick 可以使用，比如说，我们可以把通用公式修改一下：

其中，为的下采样，比如说可以利用 pooling，这样就可以减少 1/4 的 pair-wise 的计算量了。

这个 trick 不会改变 non-local 的行为，但是可以使得计算更加稀疏，通常会在上图中的后面增加一层 max pooling 层来实现。

3.Experiments

由于视频分类的实验，所以简单看一下就行。

首先是动力学行为分类的多个实验：

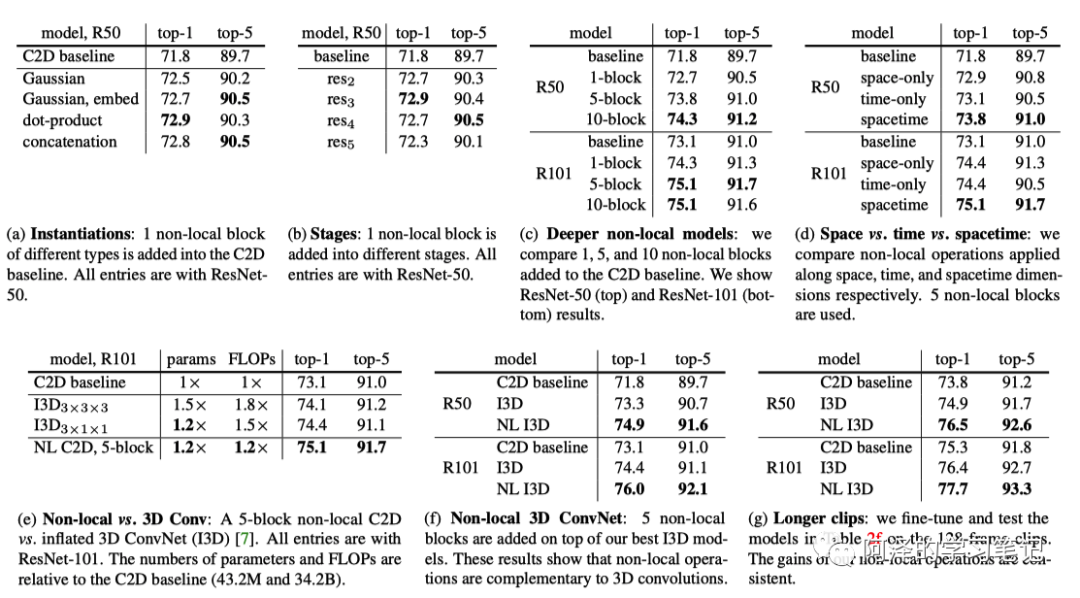
然后是模型与 baseline 的对比：

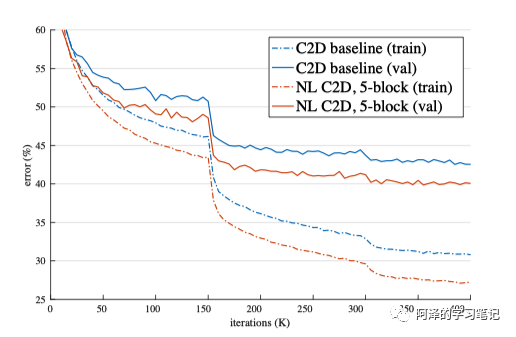
然后是不同模型之间的对比：

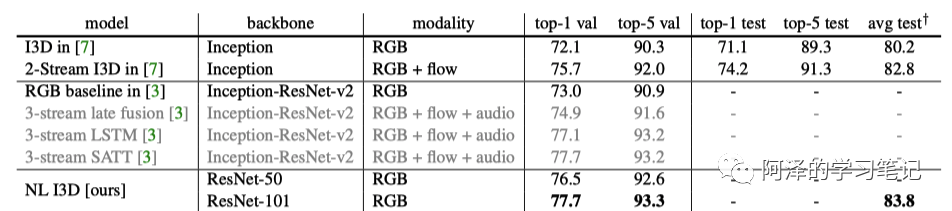
4.Conclusion

总结：作者根据非局部均值滤波方法提出了非局部神经网络（NLNN），综合考虑节点间不同位置之间的关系，同时也具有较强的灵活性，支持自定义相似函数，并支持在不改变网络结构的情况下以残差的形式接入到现有网络中，最后通过实验表明，这种非局部运算的框架具有非常显著的效果。

这篇文章思路总的来说还是比较清晰，模块也非常简单，由于 NLNN 支持可变输入大小，所以也可以无缝衔接到 GNN 中。

5.Reference

Wang X, Girshick R, Gupta A, et al. Non-local neural networks[C]//Proceedings of the IEEE conference on computer vision and pattern recognition. 2018: 7794-7803.
《Non-local neural networks》
《video-nonlocal-net》

推荐阅读

AINLP年度阅读收藏清单

当当四折购书，推荐一份书单

模型压缩实践收尾篇——模型蒸馏以及其他一些技巧实践小结

中文命名实体识别工具（NER）哪家强？

学自然语言处理，其实更应该学好英语

斯坦福大学NLP组Python深度学习自然语言处理工具Stanza试用

太赞了！Springer面向公众开放电子书籍，附65本数学、编程、机器学习、深度学习、数据挖掘、数据科学等书籍链接及打包下载

数学之美中盛赞的 Michael Collins 教授，他的NLP课程要不要收藏？

自动作诗机&藏头诗生成器：五言、七言、绝句、律诗全了

模型压缩实践系列之——bert-of-theseus，一个非常亲民的bert压缩方法

这门斯坦福大学自然语言处理经典入门课，我放到B站了

征稿启示 | 稿费+GPU算力+星球嘉宾一个都不少

关于AINLP

AINLP 是一个有趣有AI的自然语言处理社区，专注于 AI、NLP、机器学习、深度学习、推荐算法等相关技术的分享，主题包括文本摘要、智能问答、聊天机器人、机器翻译、自动生成、知识图谱、预训练模型、推荐系统、计算广告、招聘信息、求职经验分享等，欢迎关注！加技术交流群请添加AINLPer(id：ainlper)，备注工作/研究方向+加群目的。