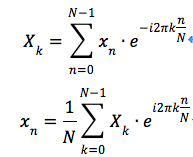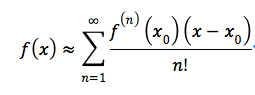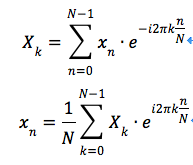细讲傅立叶变换
【注】:阅读该文章之前,建议先阅读笔者的前几篇文章:指数函数和自然对数、揭秘自然对数(ln)、从群论角度理解欧拉公式。
>>>>
个人看来,傅里叶变换是最深刻的见解之一。不幸的是,这个意义被隐藏在晦涩难懂的无穷级数中:
与其直接理解这些复杂的符号,不如让我们从生活出发,直观地理解它。
平时做饭的时候,比如做一个蛋炒饭,需要蛋,需要饭,还需要盐巴等等,而通过某种方式将这些混合起来,就变成了蛋炒饭。
如果是从业多年的厨师,你给他个蛋炒饭,他能告诉你,这蛋炒饭由哪些原料烹饪而成。而傅里叶也具备这样的能力。
当你给它一个信号(或函数),傅里叶变换能采用基于时间的模式,测量该信号(或函数)的每一个可能周期,告诉你组成该信号(或函数)的循环周期的振幅、偏移量和旋转速度等“原料”。
傅里叶变换给予我们一种新思维,让我们从思考“这是什么”转变为思考“这是如何产生的”。
那么,傅里叶变换是如何找到各个周期函数的“原料”的呢?这就是接下来要讨论的问题了。
假设我们有很多过滤网,上面的孔径大小不同,将蛋炒饭往过滤网上一倒
第一个,网孔最大的过滤网把蛋过滤了出来
第二个,网孔适中的过滤网把饭过滤了出来
第三个,网孔较小的过滤网把盐巴过滤了出来
………………
通过无数孔径不一的过滤网,不同“原料”被过滤出来,而这些过滤网统称为“过滤器(filter)”。
傅里叶是这么说的:“任何信号(或函数)都可以转换成无穷多个周期函数的和。”
【题外话】:笔者最喜欢的两个数学家分别是“泰勒”和“傅里叶”,他们的两个定理貌似揭示了世界的真理。
泰勒说:“任何函数都可以转换成无穷多个幂函数的和。”
“泰勒的这句话,给后来计算机的发展带来了巨大贡献,举个例子,计算机并没办法计算类似于sin、cos这样的函数,只能通过将他们转换为各个幂函数的和来实现。”
傅里叶说:“任何信号(或函数)都可以转换成无穷多个周期函数的和。”这句话的涵义,我们后面会慢慢细讲。
傅里叶变换用滤波器把一个基于时间的信号(或函数)的每个“圆形原料”分解出来。
【注】:所谓“圆形原料”,思考一下,我们高中所学的圆周运动,它是否就包含了一定的循环周期、振幅、偏移量和旋转速度等“原料”?所以这里用“圆形原料”指代这些“原料”。
如果地震波可被分解,找出不同的振幅和速度,那么我们可以针对地震的特定振幅和速度设计对应的抗震建筑物。
如果声波可被分解成低音和高音,我们就可以放大我们关心的部分,缩小我们不关心的部分。
"比如你喜欢小提琴,那便可以提高高音部分,隐去低音部分。
如果你喜欢低音贝斯,那么你就可以提高低音部分,隐去高音部分。"
如果计算机数据可以用震荡波形表示,且其中包含可忽略的数据,那么就可以用傅里叶变换滤去不重要的数据。这在数据科学中被叫为“数据滤波器”。
如果是收音机的无线电波,那么我们就可以收听到特定频率的广播。
傅里叶变换在工程中的应用是十分广泛的,以上举例的只是小小一部分,希望能助于你们理解傅里叶变换背后的根源。
我们重新看看刚刚的公式


由此我们可以推出
不难看出,傅里叶变换公式可以这么理解:
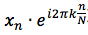
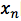
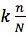
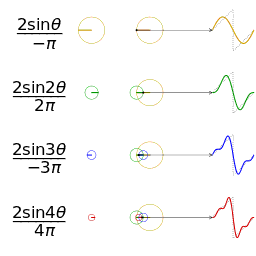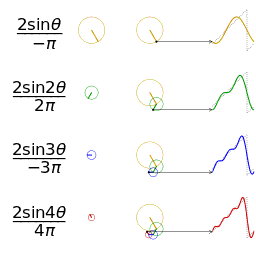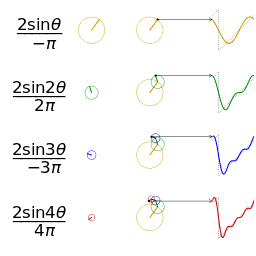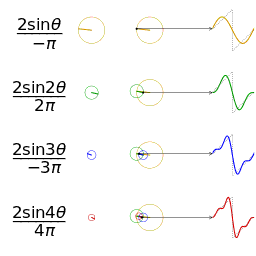
把这些不同单位向量的旋转叠加起来就是原信号
那么将原信号分解为多个圆相加是什么意思呢?
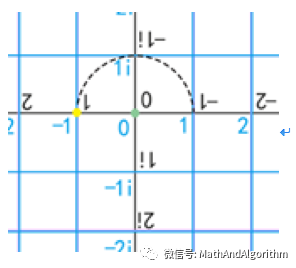
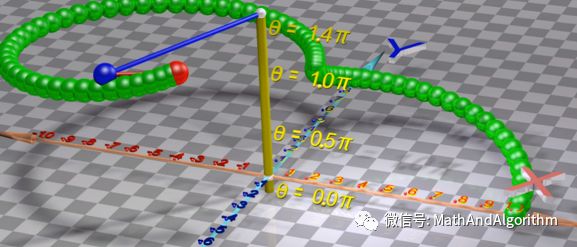
我们这么看,首先我们建立一个X轴和Y轴,并且再建立一个
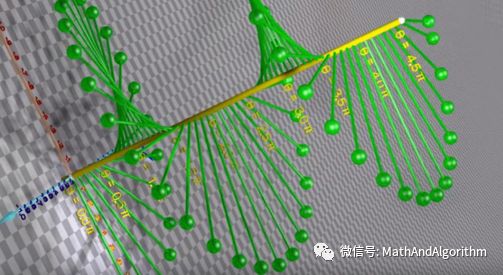
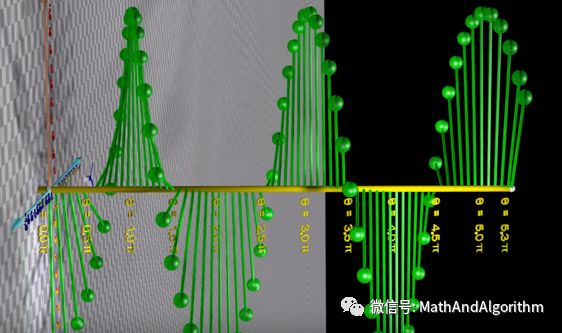
一个小球以轴为圆心,绿线为半径进行旋转,并且边旋转边上升。
接下来我们对坐标进行一个旋转,从另外一个角度来看看这个旋转过程
我们似乎发现了什么,我们对坐标继续的进行旋转,没错这就是我们的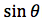
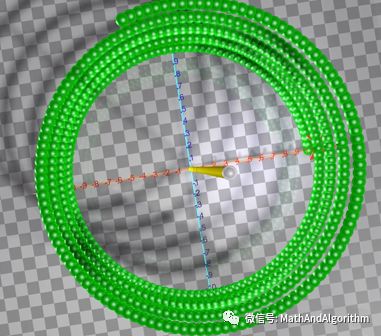
而从坐标系上方往下看是这样子的
他是由一个一个的圆形组成的,而傅里叶变换就是将不同种类的圆形分解出来。
现在我们在加上一个红色的圆
同样的,让他们一起旋转起来
换个角度来看,这就是

这里有一种动图,大家可以更好的理解这个过程。
所以,我们很直观的发现,傅里叶变换其实就是一个找圆的过程,将不同的信号(或函数)分解成不同的圆形,当他们叠加起来就又变回我们原有的信号(或函数)。
∑编辑:Gemini
算法数学之美微信公众号欢迎赐稿
稿件涉及数学、物理、算法、计算机、编程等相关领域
稿件一经采用,我们将奉上稿酬。
投稿邮箱:math_alg@163.com