“让Keras更酷一些!”:分层的学习率和自由的梯度
作者丨苏剑林
单位丨广州火焰信息科技有限公司
研究方向丨NLP,神经网络
个人主页丨kexue.fm
高举“让 Keras 更酷一些!”大旗,让 Keras 无限可能。
今天我们会用 Keras 做到两件很重要的事情:分层设置学习率和灵活操作梯度。
首先是分层设置学习率,这个用途很明显,比如我们在 fine tune 已有模型的时候,有些时候我们会固定一些层,但有时候我们又不想固定它,而是想要它以比其他层更低的学习率去更新,这个需求就是分层设置学习率了。
对于在 Keras 中分层设置学习率,网上也有一定的探讨,结论都是要通过重写优化器来实现。显然这种方法不论在实现上还是使用上都不友好。
然后是操作梯度。操作梯度一个最直接的例子是梯度裁剪,也就是把梯度控制在某个范围内,Keras 内置了这个方法。但是 Keras 内置的是全局的梯度裁剪,假如我要给每个梯度设置不同的裁剪方式呢?甚至我有其他的操作梯度的思路,那要怎么实施呢?不会又是重写优化器吧?
本文就来为上述问题给出尽可能简单的解决方案。
分层的学习率
对于分层设置学习率这个事情,重写优化器当然是可行的,但是太麻烦。如果要寻求更简单的方案,我们需要一些数学知识来指导我们怎么进行。
参数变换下的优化
首先我们考虑梯度下降的更新公式:
其中 L 是带参数 θ 的 loss 函数,α 是学习率,是梯度,有时候我们也写成
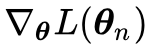
然后我们考虑变换 θ=λϕ,其中 λ 是一个固定的标量,ϕ 也是参数。现在我们来优化 ϕ,相应的更新公式为:
其中第二个等号其实就是链式法则。现在我们在两边乘上 λ,得到:
对比 (1) 和 (3),大家能明白我想说什么了吧:
在 SGD 优化器中,如果做参数变换 θ=λϕ,那么等价的结果是学习率从 α 变成了
。
不过,在自适应学习率优化器(比如 RMSprop、Adam 等),情况有点不一样,因为自适应学习率使用梯度(作为分母)来调整了学习率,抵消了一个 λ,从而(请有兴趣的读者自己推导一下):
在 RMSprop、Adam 等自适应学习率优化器中,如果做参数变换 θ=λϕ,那么等价的结果是学习率从 α 变成了 λα。
移花接木调整学习率
有了前面这两个结论,我们就只需要想办法实现参数变换,而不需要自己重写优化器,来实现逐层设置学习率了。
实现参数变换的方法也不难,之前我们在《 “让Keras更酷一些!”:随意的输出和灵活的归一化》[1] 一文讨论权重归一化的时候已经讲过方法了。因为 Keras 在构建一个层的时候,实际上是分开了 build 和 call 两个步骤,我们可以在 build 之后插一些操作,然后再调用 call 就行了。
下面是一个封装好的实现:
import keras.backend as K
class SetLearningRate:
"""层的一个包装,用来设置当前层的学习率
"""
def __init__(self, layer, lamb, is_ada=False):
self.layer = layer
self.lamb = lamb # 学习率比例
self.is_ada = is_ada # 是否自适应学习率优化器
def __call__(self, inputs):
with K.name_scope(self.layer.name):
if not self.layer.built:
input_shape = K.int_shape(inputs)
self.layer.build(input_shape)
self.layer.built = True
if self.layer._initial_weights is not None:
self.layer.set_weights(self.layer._initial_weights)
for key in ['kernel', 'bias', 'embeddings', 'depthwise_kernel', 'pointwise_kernel', 'recurrent_kernel', 'gamma', 'beta']:
if hasattr(self.layer, key):
weight = getattr(self.layer, key)
if self.is_ada:
lamb = self.lamb # 自适应学习率优化器直接保持lamb比例
else:
lamb = self.lamb**0.5 # SGD(包括动量加速),lamb要开平方
K.set_value(weight, K.eval(weight) / lamb) # 更改初始化
setattr(self.layer, key, weight * lamb) # 按比例替换
return self.layer(inputs)使用示例:
x_in = Input(shape=(None,))
x = x_in
# 默认情况下是x = Embedding(100, 1000, weights=[word_vecs])(x)
# 下面这一句表示:后面将会用自适应学习率优化器,并且Embedding层以总体的十分之一的学习率更新。
# word_vecs是预训练好的词向量
x = SetLearningRate(Embedding(100, 1000, weights=[word_vecs]), 0.1, True)(x)
# 后面部分自己想象了~
x = LSTM(100)(x)
model = Model(x_in, x)
model.compile(loss='mse', optimizer='adam') # 用自适应学习率优化器优化几个注意事项:
1. 目前这种方式,只能用于自己动手写代码来构建模型的时候插入,无法对建立好的模型进行操作;
2. 如果有预训练权重,有两种加载方法。第一种是像刚才的使用示例一样,在定义层的时候通过 weights 参数传入;第二种方法是建立好模型后(已经在相应的地方插入好 SetLearningRate),用 model.set_weights (weights) 来赋值,其中 weights 是“在 SetLearningRate 的位置已经被除以了 λ 或的原来模型的预训练权重”;
3. 加载预训练权重的第二种方法看起来有点不知所云,但如果你已经理解了这一节的原理,那么应该能知道我在说什么。因为设置学习率是通过 weight * lamb 来实现的,所以 weight 的初始化要变为 weight / lamb;
4. 这个操作基本上不可逆,比如你一开始设置了 Embedding 层以总体的 1/10 比例的学习率来更新,那么很难在这个基础上,再将它改为 1/5 或者其他比例。(当然,如果你真的彻底搞懂了这一节的原理,并且也弄懂了加载预训练权重的第二种方法,那么还是有办法的,那时候相信你也能搞出来);
5. 这种做法有以上限制,是因为我们不想通过修改或者重写优化器的方式来实现这个功能。如果你决定要自己修改优化器,请参考《“让Keras更酷一些!”:小众的自定义优化器》[2]。
自由的梯度操作
在这部分内容中,我们将学习对梯度的更为自由的控制。这部分内容涉及到对优化器的修改,但不需要完全重写优化器。
Keras优化器的结构
要修改优化器,必须先要了解 Keras 优化器的结构。在《“让Keras更酷一些!”:小众的自定义优化器》[2] 一文我们已经初步看过了,现在我们重新看一遍。
Keras 优化器代码:
https://github.com/keras-team/keras/blob/master/keras/optimizers.py
随便观察一个优化器,就会发现你要自定义一个优化器,只需要继承 Optimizer 类,然后定义 get_updates 方法。但本文我们不想做新的优化器,只是想要对梯度有所控制。可以看到,梯度的获取其实是在父类 Optimizer 的 get_gradients 方法中:
def get_gradients(self, loss, params):
grads = K.gradients(loss, params)
if None in grads:
raise ValueError('An operation has `None` for gradient. '
'Please make sure that all of your ops have a '
'gradient defined (i.e. are differentiable). '
'Common ops without gradient: '
'K.argmax, K.round, K.eval.')
if hasattr(self, 'clipnorm') and self.clipnorm > 0:
norm = K.sqrt(sum([K.sum(K.square(g)) for g in grads]))
grads = [clip_norm(g, self.clipnorm, norm) for g in grads]
if hasattr(self, 'clipvalue') and self.clipvalue > 0:
grads = [K.clip(g, -self.clipvalue, self.clipvalue) for g in grads]
return grads其中方法中的第一句就是获取原始梯度的,后面则提供了两种梯度裁剪方法。不难想到,只需要重写优化器的 get_gradients 方法,就可以实现对梯度的任意操作了,而且这个操作不影响优化器的更新步骤(即不影响 get_updates 方法)。
处处皆对象:覆盖即可
怎么能做到只修改 get_gradients 方法呢?这得益于 Python 的哲学——“处处皆对象”。Python 是一门面向对象的编程语言,Python 中几乎你能碰到的一切变量都是一个对象。我们说 get_gradients 是优化器的一个方法,也可以说 get_gradients 的一个属性(对象),既然是属性,直接覆盖赋值即可。
我们来举一个最粗暴的例子(恶作剧):
def our_get_gradients(loss, params):
return [K.zeros_like(p) for p in params]
adam_opt = Adam(1e-3)
adam_opt.get_gradients = our_get_gradients
model.compile(loss='categorical_crossentropy',
optimizer=adam_opt)
其实这样做的事情很无聊,就是把所有梯度置零了(然后你怎么优化它都不动了),但这个恶作剧例子已经足够有代表性了——你可以将所有梯度置零,你也可以将梯度做任意你喜欢的操作。比如将梯度按照 l1 范数而非 l2 范数裁剪,又或者做其他调整。
假如我只想操作部分层的梯度怎么办?那也简单,你在定义层的时候需要起一个能区分的名字,然后根据 params 的名字做不同的操作即可。都到这一步了,我相信基本是“一法通,万法皆通”的了。
飘逸的Keras
也许在很多人眼中,Keras 就是一个好用但是封装得很“死”的高层框架,但在我眼里,我只看到了它无限的灵活性——那是一个无懈可击的封装。
相关链接
[1] https://kexue.fm/archives/6311
[2] https://kexue.fm/archives/5879
点击以下标题查看作者其他文章:

让你的论文被更多人看到
如何才能让更多的优质内容以更短路径到达读者群体,缩短读者寻找优质内容的成本呢? 答案就是:你不认识的人。
总有一些你不认识的人,知道你想知道的东西。PaperWeekly 或许可以成为一座桥梁,促使不同背景、不同方向的学者和学术灵感相互碰撞,迸发出更多的可能性。
PaperWeekly 鼓励高校实验室或个人,在我们的平台上分享各类优质内容,可以是最新论文解读,也可以是学习心得或技术干货。我们的目的只有一个,让知识真正流动起来。
📝 来稿标准:
• 稿件确系个人原创作品,来稿需注明作者个人信息(姓名+学校/工作单位+学历/职位+研究方向)
• 如果文章并非首发,请在投稿时提醒并附上所有已发布链接
• PaperWeekly 默认每篇文章都是首发,均会添加“原创”标志
📬 投稿邮箱:
• 投稿邮箱:hr@paperweekly.site
• 所有文章配图,请单独在附件中发送
• 请留下即时联系方式(微信或手机),以便我们在编辑发布时和作者沟通
🔍
现在,在「知乎」也能找到我们了
进入知乎首页搜索「PaperWeekly」
点击「关注」订阅我们的专栏吧
关于PaperWeekly
PaperWeekly 是一个推荐、解读、讨论、报道人工智能前沿论文成果的学术平台。如果你研究或从事 AI 领域,欢迎在公众号后台点击「交流群」,小助手将把你带入 PaperWeekly 的交流群里。
▽ 点击 | 阅读原文 | 查看作者博客