范式大学｜机器学习：1 亿的数据量怎么选模型，10 亿呢？

小明是数据科学家实习生，最近他遇到一个问题：

 

当他完成小数据的建模时，一个简单的线性 SVM 就能够取得很好的效果。但是当数据量增大到 1 个亿，哪怕他用尽吃奶的力气调参，效果也上不去了。

 

小明的导师知道了情况，他和小明解释说：“出现这个情况，是因为模型的 VC 维不够大。”

什么是VC维？

VC 维的概念十分久远，最早是由名字很难读的Vladimir Vapnik 和 AlexeyChervonenk 发明的，那时候是 1971 年。

 

在 VC 维的发展历史中，有一个得意弟子叫 SVM，在 1993 年由Corinna Cortes 和 Vapnik 提出，并带来了SVM 和 Neural Network 长达 12 年的激烈竞争。后面深度学习在 2005 年兴起，关于VC 维的概念就越来越少人关注了。

 

但 VC 维其实是机器学习的基础，因为它解释了为什么某机器学习方法是可学习的？为什么会有过拟合？以及我们拿什么来衡量机器学习的模型复杂度？机器学习模型需要多少数据量等等。

 

我们尝试给 VC 维一个简单的表述：将N个点进行分类，如分成两类，那么可以有2^N种分法，即可以理解成有2^N个学习问题。若存在一个假设H，能准确无误地将2^N种问题进行分类。那么这些点的数量N，就是H的VC维。 

 

举个例子：

 

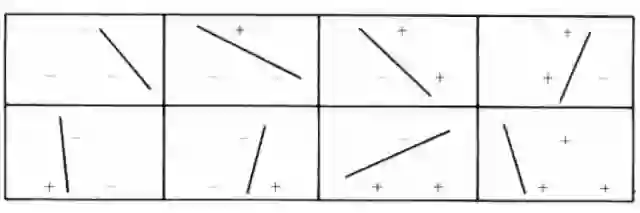
在一个2D空间中，我们考虑一个线性的分类模型，也就是一条直线。现在有一个由三个不共线点组成的数据集，考虑其所有正负例分配方案一共是2^3=8种，如下图所示。可以看到，对于任意一种分配方案，线性的分类模型都可以完美地将正负例分开，因此该模型能有效分类三个点的数据集。

那么包含四个点的数据集呢？读者可以动手画一画，给定四个固定位置的数据点，一定存在某个正负例分配方案，仅借助一条直线是没办法将正负例完全分开的。更进一步，容易证明，不管这四个点的位置怎么摆，总是可以把某些点定为正，某些点定为负，然后一条直线不能分开他们。

 

因此，该线性模型在2D平面上可以有效分类3个点的数据集，而对于任意4个点的数据集则无能为力。

 

所以我们定义：该模型在2D平面上的VC维就是3。

完整内容请点击“阅读原文”

转自：第四范式