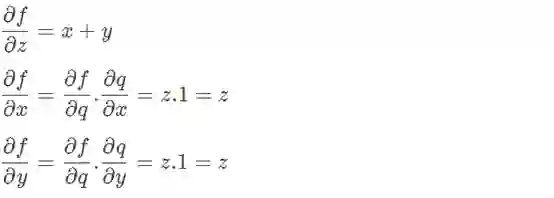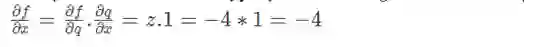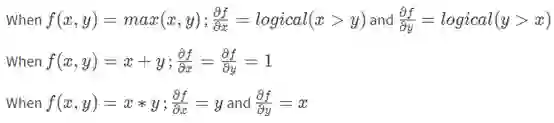关于反向传播在Python中应用的入门教程

Python部落(python.freelycode.com)组织翻译，禁止转载，欢迎转发。

我来这里的目的是为了测试我对于Karpathy的博客《骇客的神经网络指导》以及Python的理解，也是为了掌握最近精读的Derek Banas的文章《令人惊奇的注释代码博览》。作为一个沉浸在R语言和结构化数据的经典统计学习方法的人，我对于Python和神经网络都很陌生，所以最好不要对个人能力产生错觉，以为通过阅读就可以掌握事物。因此，开始写代码吧。

神经门

理解神经网络中任何节点的一种方法是把它当作门，它接收一个或多个输入，并产生一个输出，就像一个函数。

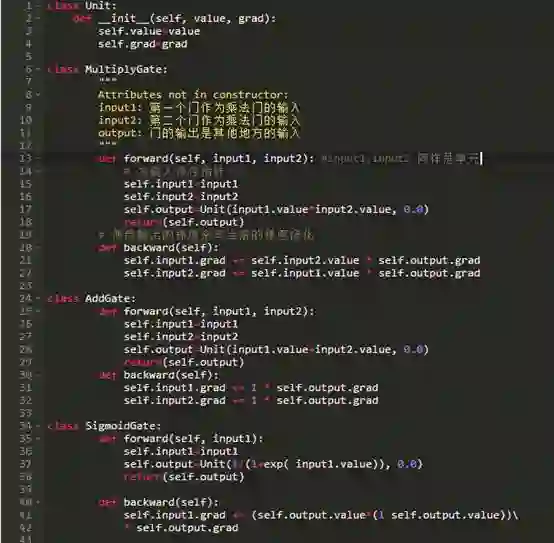
例如，考虑一个接受x和y作为输入的门，并计算：f(x,y) = x * y，让我们一起在Python中实现它：

类似地，我们可以实现一个门来计算它的两个输入的和。

和一个计算两个输入最大值的门。

最优化问题

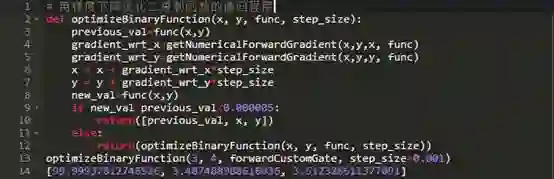
考虑到电路的目标是最大化输出。这其实是神经网络的优化问题（实际上是最小化损失函数，但差别是微不足道的，这与最大化负损失函数相同）。现在，关键在于如何确定修改一点点输入，就可以使输出变大一点。如果我们能够设计出一种识别的方法，可以一次又一次地尝试这种方法来获得更大的输出值，直到我们碰到南墙，输出停止增加。在那时，我们可以说我们已经将产出最大化，或者说至少在局部上达到了。

用一个只有一个门的简单的电路来说明，就是前向乘法门

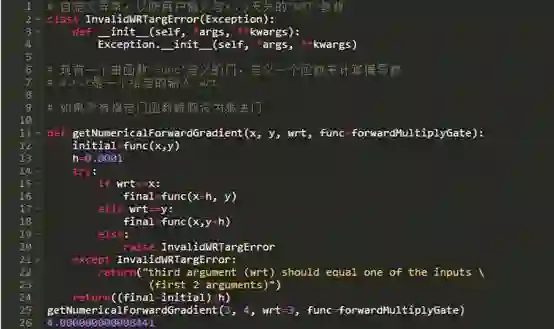
假设上文定义的前向乘法门是我们在神经网络里的唯一门。如何来调整每个输入，完全取决于输出对输入的更改的敏感性(或响应)。因为就像之前所展示的那样，输出本质上是输入的函数，输出对每个输入的敏感性就是那个输入的偏导数，让我们来计算一下：

当x=3和y=4时，乘法门的梯度，等于4，因为del(xy)/del(x)=y，也就是4。

由于梯度肯定是正的，所以增大一点x理应会增加输出。让我们来试试:

输出果然增加了，和我们设想的一样

这只是一个简单门。如果我们让门来实现函数f(x): f(x) = 100 - (x-y)^2会怎样呢

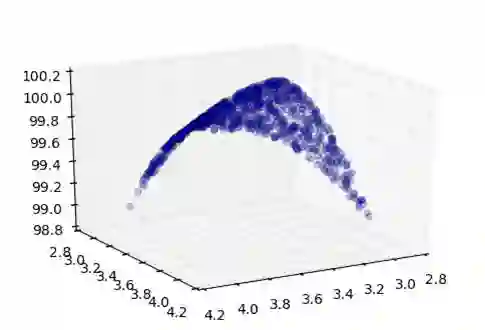
如果我们给这个门提供的输入是3和4，按道理它应该尽量让x和y更接近，这样输出才会最大化。这个函数在x=y上的最大化是不重要的

请参见下面的图片:

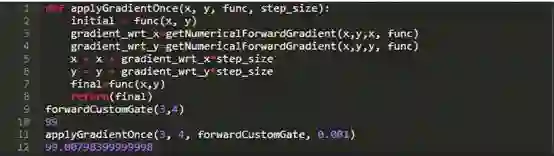
现在让我们定义这个门，看看我们的梯度计算和输入修改的方法是否有助于增加这个门的输出。

正如预期的那样，在梯度暗示的方向上对输入进行一些修改，结果会产生更高的输出。现在让我们来多做几次，几十次，直到产量的提高或增加都不再明显了

也和预期一样，以这种方式来进行优化，让x从3提升到3.49同时让y从4降到3.51，从而使输出达到了99.999。

使用解析梯度

到目前为止,我们已经证明了梯度下降法优化的一个应用，getNumericalForwardGradient函数来计算梯度数值。在实践中，神经网络包含大量复杂的门，这些门的数值的每次计算都变得非常昂贵。因此，我们经常使用解析梯度，它更准确，计算量也更少。

这就提出了新的问题:如果表达式复杂到，即使数学方法也很难求解梯度的解析解。我们将看到，为了处理这种情况，我们可以计算出一些简单表达式的解析梯度，然后应用链式法则。

多神经门电路

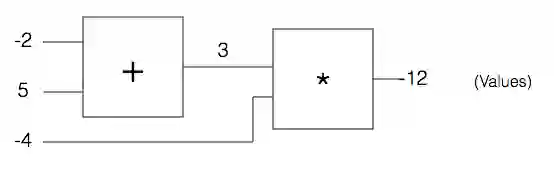
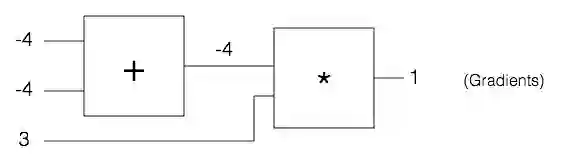
让我们考虑一个电路门，以x，y和z分别作为输入和输出。

实际上，这是两个基本门的合体：一个是加门，输入为x和y，另一个是乘积门，输入为r和加门的输出q。我们可以定义这个门如下:

上图来源于 http://karpathy.github.io/neuralnets/

反向传播

优化这个电路本来是需要我们计算整个电路的梯度。现在相反，我们将计算每个组件门的梯度，然后应用链式法则来获得整个电路的梯度。

在这里,q只是一个输入为x和y的前向加法门, f是一个输入为z和q的前向乘法门。上述最后两个方程是整个的关键: 当使用x(或y)计算整个电路的梯度时，我们仅仅计算了关于x(或y)的门q的梯度，并用一个因子将其放大，就等于与门q的输出有关的电路的梯度。

对于这个电路的输入，x=-2，y=5，z=-4，这不难计算

让我们看看这里发生了什么。照此∂x/∂q就等于1，即，增加x从而增加了门的输出q。然而，在较大的电路中(f)输出是由于输出q的减少而增加的，因为∂f/∂q= z = -4是一个负数。因此，我们的目标是通过减少q来实现最大的电路f的输出，同样x的值也需要减少。

在这个电路中展示的很明显，为了计算任何输入的梯度，我们需要根据每个输入，计算出那些直接接受输入的门的梯度，然后将电路的每个门的梯度结果相乘(链式法则)。

但是在一个更复杂的电路中，在输出阶段之前，这个门可能会通向多个其他门，所以最好先从输出阶段开始进行逆向链式计算。(反向传播)

上图来源于http://karpathy.github.io/neuralnets/

看过我们如何使用链式法则后，我们现在可以把重点放在一些简单门的局部梯度上:

我刚意识到我们好久都没有写代码了。哦。现在，我们将对我们所讨论的一切进行代码化，来看看反向传播使用链式法则到底是如何帮助我们计算相同的梯度。

在定义了门和单元之后，让我们运行正向传递来生成输出值：

现在，让我们运行反向传递来破译梯度df/dx:

现在我们已经从零开始在一个简单的电路上实现了反向传播，并且看到了如何利用链式法则来获得一个更大的电路的梯度。实在是太有趣啦！

英文原文：https://sushant-choudhary.github.io/blog/2017/11/25/a-friendly-introduction-to-backrop-in-python.html
译者：任宇は神様