超详细的语义分割中的Loss大盘点

会员服务 ·

超详细的语义分割中的Loss大盘点

2020 年 8 月 21 日 极市平台

↑ 点击蓝字关注极市平台

作者丨BBuf@知乎

来源丨https://zhuanlan.zhihu.com/p/103426335

极市导读

作为一篇超详细的大盘点，本文介绍了超过十种语义分割的常见Loss及组合。大部分介绍附有代码实现，帮助大家掌握新的损失函数并进行应用。>>>极市七夕粉丝福利活动：炼丹师们，七夕这道算法题，你会解吗？

前言

前两天介绍了一下Contrastive Loss、Triplet Loss以及Center Loss。今天正好是周六，时间充分一点，我就来大概盘点一下 语义分割的常见Loss，希望能为大家训练语义分割网络的时候提供一些关于Loss方面的知识。此文只为抛砖引玉，一些Loss笔者暂时也没有进行试验，之后做了实验有了实验结果会继续更新。

交叉熵Loss

其中，表示类别数，是一个 one-hot向量，元素只有和两种取值，如果该类别和样本的类别相同就取，否则取，至于表示预测样本属于的概率。

当类别数等于的时候，这个损失就是二元交叉熵，在Pytorch中提供了一个单独的实现。

交叉熵Loss可以用在大多数语义分割场景中，但它有一个明显的缺点，那就是对于只用分割前景和背景的时候，当前景像素的数量远远小于背景像素的数量时，即的数量远大于的数量，损失函数中的成分就会占据主导，使得模型严重偏向背景，导致效果不好。

代码实现如下：

   
   
     
    
    
      #二值交叉熵，这里输入要经过sigmoid处理
    
    
      import torch
    
    
      import torch.nn as nn
    
    
      import torch.nn.functional as F
    
    
      nn.BCELoss(F.sigmoid(input), target)
    
    
      #多分类交叉熵, 用这个 loss 前面不需要加 Softmax 层
    
    
      nn.CrossEntropyLoss(input, target)

带权交叉熵Loss

带权重的交叉熵Loss，公式为：

可以看到只是在交叉熵Loss的基础上为每一个类别添加了一个权重参数，其中的计算公式为：其中表示总的像素个数，而表示GT类别为的像素个数。这样相比于原始的交叉熵Loss，在样本数量不均衡的情况下可以获得更好的效果。

Focal Loss

何凯明团队在RetinaNet论文中引入了Focal Loss来解决 难易样本数量不平衡，我们来回顾一下。我们知道，One-Stage的目标检测器通常会产生 10k数量级的框，但只有极少数是正样本，正负样本数量非常不平衡。我们在计算分类的时候常用的损失——交叉熵的公式如下：

为了解决 正负样本数量不平衡的问题，我们经常在二元交叉熵损失前面加一个参数，即：

虽然平衡了正负样本的数量，但实际上，目标检测中大量的候选目标都是易分样本。这些样本的损失很低，但是由于数量极不平衡，易分样本的数量相对来讲太多，最终主导了总的损失。

因此，这篇论文认为 易分样本（即，置信度高的样本）对模型的提升效果非常小，模型应该主要关注与那些难分样本 。所以Focal Loss横空出世了。一个简单的想法就是只要我们将高置信度样本的损失降低一些就好了吧？也即是下面的公式：

我们取等于2来感受一下，如果，那么, ，损失降低了1000倍。最终Focal Loss还结合了公式(2)，这很好理解，公式(3)解决了难易样本的不平衡，公式(2)解决了正负样本的不平衡，将公式（2）与（3）结合使用，同时解决正负难易2个问题！所以最终Focal Loss的形式如下：

下面这张图展示了Focal Loss取不同的时的损失函数下降。

实验结果展示，当，时，效果最好，这样损失函数训练的过程中关注的样本优先级就是正难>负难>正易>负易了。

虽然在RetinaNet中取是最好的，但是不代表这个参数在我们的分割任务和其他样本上是最好的，我们需要手动调整这个参数，另外Focal Loss在分割任务上似乎是 只适合于二分类的情况。

Focal Loss的Pytorch代码实现如下：

   
   
     
    
    
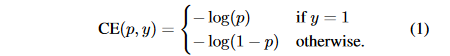
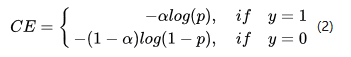
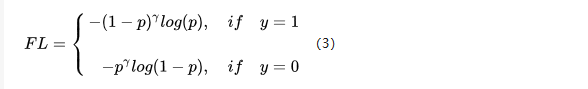
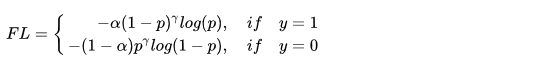
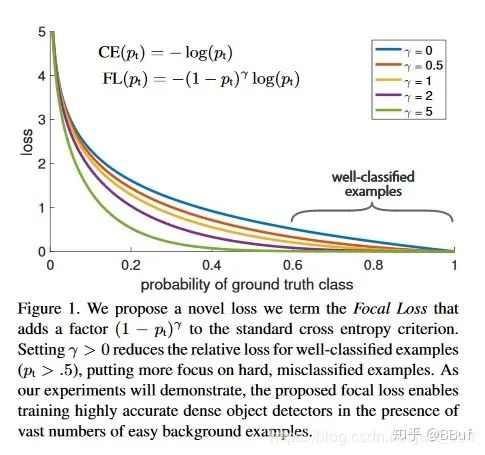
      class FocalLoss(nn.Module):
    
    
          def __init__(self, gamma=0, alpha=None, size_average=True):
    
    
              super(FocalLoss, self).__init__()
    
    
              self.gamma = gamma
    
    
              self.alpha = alpha
    
    
              if isinstance(alpha,(float,int,long)): self.alpha = torch.Tensor([alpha,1-alpha])
    
    
              if isinstance(alpha,list): self.alpha = torch.Tensor(alpha)
    
    
              self.size_average = size_average
    
    
      

    
    
          def forward(self, input, target):
    
    
              if input.dim()>2:
    
    
                  input = input.view(input.size(0),input.size(1),-1)  # N,C,H,W => N,C,H*W
    
    
                  input = input.transpose(1,2)    # N,C,H*W => N,H*W,C
    
    
                  input = input.contiguous().view(-1,input.size(2))   # N,H*W,C => N*H*W,C
    
    
              target = target.view(-1,1)
    
    
      

    
    
              logpt = F.log_softmax(input)
    
    
              logpt = logpt.gather(1,target)
    
    
              logpt = logpt.view(-1)
    
    
              pt = Variable(logpt.data.exp())
    
    
      

    
    
              if self.alpha is not None:
    
    
                  if self.alpha.type()!=input.data.type():
    
    
                      self.alpha = self.alpha.type_as(input.data)
    
    
                  at = self.alpha.gather(0,target.data.view(-1))
    
    
                  logpt = logpt * Variable(at)
    
    
      

    
    
              loss = -1 * (1-pt)**self.gamma * logpt
    
    
              if self.size_average: return loss.mean()
    
    
              else: return loss.sum()

Dice Loss

Dice系数：根据 Lee Raymond Dice[1]命令，是用来度量集合相似度的度量函数，通常用于计算两个样本之间的像素，公式如下：分子中之所以有一个系数2是因为分母中有重复计算和的原因，最后的取值范围是。而针对我们的分割任务来说，表示的就是Ground Truth分割图像，而Y代表的就是预测的分割图像。这里可能需要再讲一下，其实除了上面那种形式还可以写成：其中分别代表真阳性，假阳性，假阴性的像素个数。
Dice Loss：公式定义为： Dice Loss使用与样本极度不均衡的情况，如果一般情况下使用Dice Loss会回反向传播有不利的影响，使得训练不稳定。
训练分割网络，例如FCN，UNet是选择交叉熵Loss还是选择Dice Loss？

假设我们用来表示预测值，而来表示真实标签值，那么交叉熵损失关于的梯度形式类似于（我会在文后给出推导），而Dice Loss的值是或，其关于的梯度形式为或，可以看到在极端情况下即和都很小的时候，计算得到的梯度值可能会非常大，即会导致训练十分不稳定。

另外一种解决类别不平衡的方法是简单的对每一个类别根据赋予不同的权重因子（如对数量少的类别赋予较大的权重因子），使得样本数量不均衡问题得到缓解（上面已经介绍过了，就是带权重的交叉熵Loss）。

这两种处理方式，哪种更好，还是建议自己针对自己的数据做一个实验。

代码实现：

   
   
     
    
    
      import torch.nn as nn
    
    
      import torch.nn.functional as F
    
    
      

    
    
      class SoftDiceLoss(nn.Module):
    
    
          def __init__(self, weight=None, size_average=True):
    
    
              super(SoftDiceLoss, self).__init__()
    
    
      

    
    
          def forward(self, logits, targets):
    
    
              num = targets.size(0)
    
    
              // 为了防止除0的发生
    
    
              smooth = 1
    
    
      

    
    
              probs = F.sigmoid(logits)
    
    
              m1 = probs.view(num, -1)
    
    
              m2 = targets.view(num, -1)
    
    
              intersection = (m1 * m2)
    
    
      

    
    
              score = 2. * (intersection.sum(1) + smooth) / (m1.sum(1) + m2.sum(1) + smooth)
    
    
              score = 1 - score.sum() / num
    
    
              return score

IOU Loss

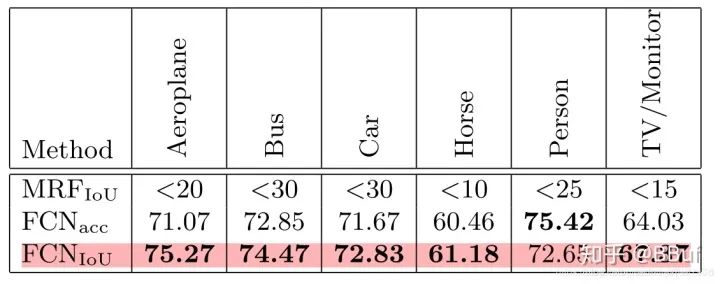
IOU Loss和Dice Loss一样属于metric learning的衡量方式，公式定义如下：

它和Dice Loss一样仍然存在训练过程不稳定的问题，IOU Loss在分割任务中应该是不怎么用的，如果你要试试的话代码实现非常简单，在上面Dice Loss的基础上改一下分母部分即可，不再赘述了。我们可以看一下将IOU loss应用到FCN上在VOC 2010上的实验结果：

可以看到IOU Loss是对大多数类别的分割结果有一定改善的，但是对 Person类却性能反而下降了。

Tversky Loss

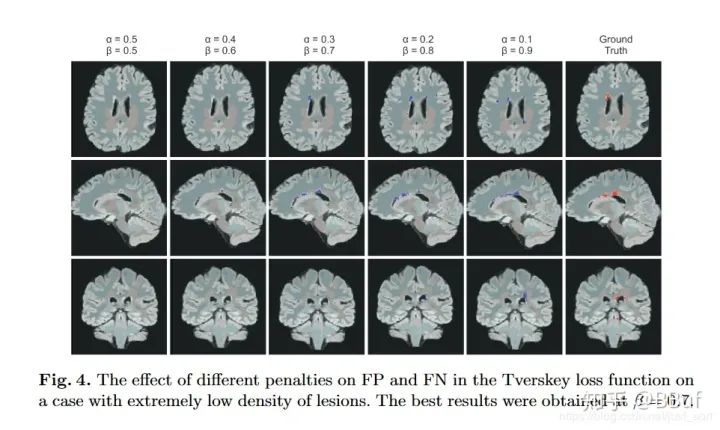
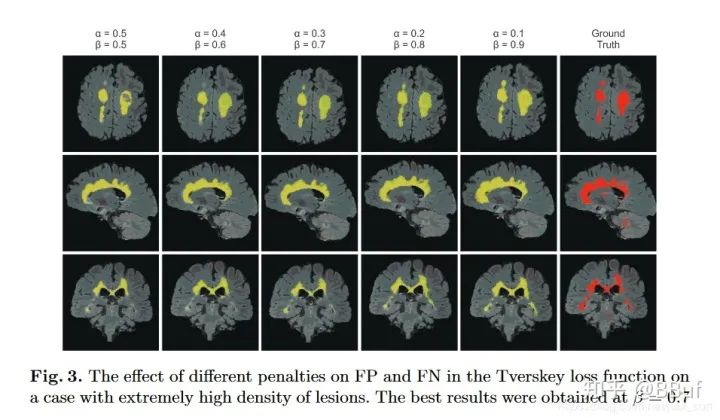
论文地址为： https://arxiv.org/pdf/1706.05721.pdf。实际上Dice Loss只是Tversky loss的一种特殊形式而已，我们先来看一下Tversky系数的定义，它是Dice系数和Jaccard系数（就是IOU系数，即）的广义系数，公式为：这里A表示预测值而B表示真实值。当和均为的时候，这个公式就是Dice系数，当和均为的时候，这个公式就是Jaccard系数。其中代表FP（假阳性），代表FN(假阴性)，通过调整和这两个超参数可以控制这两者之间的权衡，进而影响召回率等指标。下表展示了对FCN使用Tversky Loss进行病灶分割，并且取不同的和参数获得的结果，其中Sensitivity代表召回率Recall，而Specificity表示准确率Precision：

在极小的病灶下的分割效果图如下：

而在较大的病灶下的分割效果图如下：

Keras代码实现如下：

   
   
     
    
    
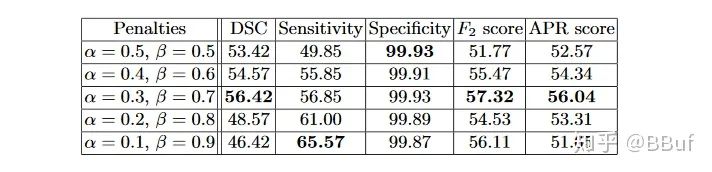
      def tversky(y_true, y_pred):
    
    
          y_true_pos = K.flatten(y_true)
    
    
          y_pred_pos = K.flatten(y_pred)
    
    
          true_pos = K.sum(y_true_pos * y_pred_pos)
    
    
          false_neg = K.sum(y_true_pos * (1-y_pred_pos))
    
    
          false_pos = K.sum((1-y_true_pos)*y_pred_pos)
    
    
          alpha = 0.7
    
    
          return (true_pos + smooth)/(true_pos + alpha*false_neg + (1-alpha)*false_pos + smooth)
    
    
      

    
    
      def tversky_loss(y_true, y_pred):
    
    
          return 1 - tversky(y_true,y_pred)

Generalized Dice loss

论文原文全程为： Generalized Overlap Measures for Evaluation and Validation in Medical Image Analysis 刚才分析过Dice Loss对小目标的预测是十分不利的，因为一旦小目标有部分像素预测错误，就可能会引起Dice系数大幅度波动，导致梯度变化大训练不稳定。另外从上面的代码实现可以发现，Dice Loss针对的是某一个特定类别的分割的损失。当类似于病灶分割有多个场景的时候一般都会使用多个Dice Loss，所以Generalized Dice loss就是将多个类别的Dice Loss进行整合，使用一个指标作为分割结果的量化指标。GDL Loss在类别数为2时公式如下：其中表示类别在第个位置的真实像素类别，而表示相应的预测概率值，表示每个类别的权重。的公式为：。

Keras代码实现：

   
   
     
    
    
      def generalized_dice_coeff(y_true, y_pred):
    
    
          Ncl = y_pred.shape[-1]
    
    
          w = K.zeros(shape=(Ncl,))
    
    
          w = K.sum(y_true, axis=(0,1,2))
    
    
          w = 1/(w**2+0.000001)
    
    
          # Compute gen dice coef:
    
    
          numerator = y_true*y_pred
    
    
          numerator = w*K.sum(numerator,(0,1,2,3))
    
    
          numerator = K.sum(numerator)
    
    
          denominator = y_true+y_pred
    
    
          denominator = w*K.sum(denominator,(0,1,2,3))
    
    
          denominator = K.sum(denominator)
    
    
          gen_dice_coef = 2*numerator/denominator
    
    
          return gen_dice_coef
    
    
      def generalized_dice_loss(y_true, y_pred):
    
    
          return 1 - generalized_dice_coeff(y_true, y_pred)

BCE + Dice Loss

即将BCE Loss和Dice Loss进行组合，在数据较为均衡的情况下有所改善，但是在数据极度不均衡的情况下交叉熵Loss会在迭代几个Epoch之后远远小于Dice Loss，这个组合Loss会退化为Dice Loss。

Focal Loss + Dice Loss

这个Loss的组合应该最早见于腾讯医疗AI实验室2018年在《Medical Physics》上发表的这篇论文： https://arxiv.org/pdf/1808.05238.pdf。论文提出了使用Focal Loss和Dice Loss来处理小器官的分割问题。公式如下：

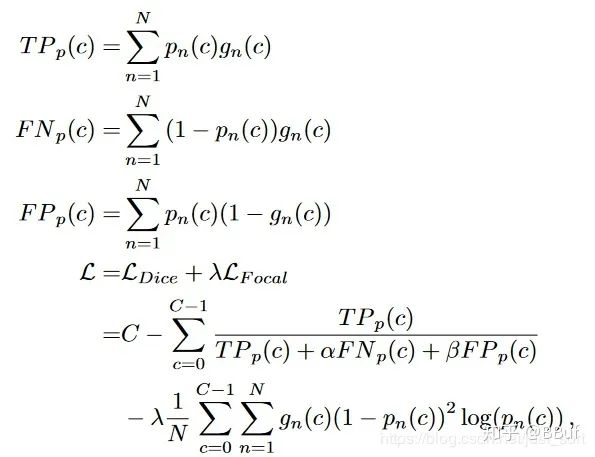
其中，，分别表示对于类别 c的真阳性，假阴性，假阳性。可以看到这里使用Focal Loss的时候，里面的两个参数直接用对于类别 c的正样本像素个数来代替。具体实验细节和效果可以去看看原论文。

Exponential Logarithmic loss

这个Loss是MICCAI 2018的论文 3D Segmentation with Exponential LogarithmicLoss for Highly Unbalanced Object Sizes提出来的，论文地址为： https://arxiv.org/abs/1809.00076。这个Loss结合了Focal Loss以及Dice loss。公式如下：

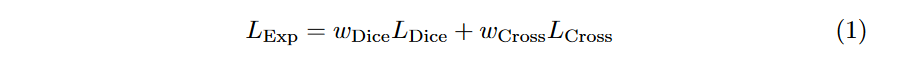
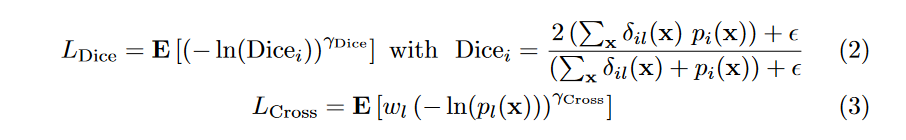
这里增加了两个参数权重分别为和，而为指数log Dice损失，为指数交叉熵损失。公式如下：

其中，表示像素位置，表示类别标签，表示位置处的ground truth类别，表示经过 softmax操作之后的概率值。其中：其中表示标签出现的频率，这个参数可以减小出现频率较高的类别权重。和可以提升函数的非线性，如Figure2所示：

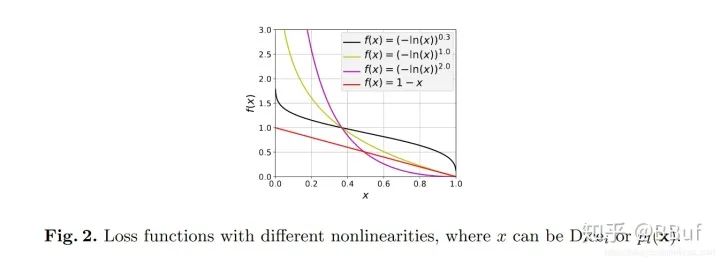
Lovasz-Softmax Loss

这是今天要介绍的最后一个Loss，Kaggle神器。这篇论文是CVPR 2018的，原地址为： https://arxiv.org/pdf/1705.08790.pdf。对原理感兴趣可以去看一下论文，这个损失是对Jaccard(IOU) Loss进行Lovaze扩展，表现更好。因为这篇文章的目的只是简单盘点一下，就不再仔细介绍这个Loss了。之后可能会单独介绍一下这个Loss，论文的官方源码见附录，使用其实不是太难。

补充（Softmax梯度计算）

在介绍Dice Loss的时候留了一个问题，交叉熵的梯度形式推导，这里给一下推导。

(1)softmax函数首先再来明确一下softmax函数，一般softmax函数是用来做分类任务的输出层。softmax的形式为: 其中表示的是第i个神经元的输出，接下来我们定义一个有多个输入，一个输出的神经元。神经元的输出为其中是第个神经元的第个权重,b是偏移值. 表示网络的第个输出。给这个输出加上一个softmax函数，可以写成: , 其中表示softmax函数的第i个输出值。这个过程可以用下图表示:

(2)损失函数 softmax的损失函数一般是选择交叉熵损失函数，交叉熵函数形式为：其中y_i表示真实的标签值 (3)需要用到的高数的求导公式

   
   
     
    
    
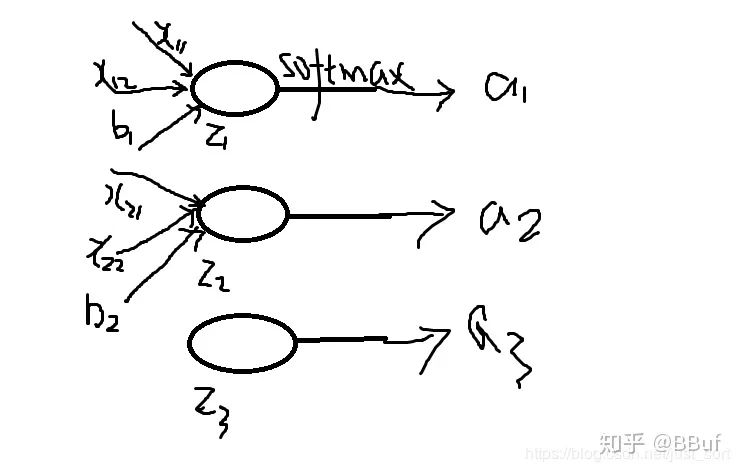
      c'=0(c为常数）
    
    
      (x^a)'=ax^(a-1),a为常数且a≠0
    
    
      (a^x)'=a^xlna
    
    
      (e^x)'=e^x
    
    
      (logax)'=1/(xlna),a>0且 a≠1
    
    
      (lnx)'=1/x
    
    
      (sinx)'=cosx
    
    
      (cosx)'=-sinx
    
    
      (tanx)'=(secx)^2
    
    
      (secx)'=secxtanx
    
    
      (cotx)'=-(cscx)^2
    
    
      (cscx)'=-csxcotx
    
    
      (arcsinx)'=1/√(1-x^2)
    
    
      (arccosx)'=-1/√(1-x^2)
    
    
      (arctanx)'=1/(1+x^2)
    
    
      (arccotx)'=-1/(1+x^2)
    
    
      (shx)'=chx
    
    
      (chx)'=shx
    
    
      （uv)'=uv'+u'v
    
    
      (u+v)'=u'+v'
    
    
      (u/)'=(u'v-uv')/^2

(3)进行推导我们需要求的是loss对于神经元输出的梯度，求出梯度后才可以反向传播，即是求: , 根据链式法则(也就是复合函数求导法则) ，初学的时候这个公式理解了很久，为什么这里是而不是呢？这里我们回忆一下softmax的公示，分母部分包含了所有神经元的输出，所以对于所有输出非i的输出中也包含了，所以所有的a都要参与计算，之后我们会看到计算需要分为和两种情况分别求导数。首先来求前半部分：接下来求第二部分的导数：

如果，
如果，。

接下来把上面的组合之后得到：。推导完成! (4)对于分类问题来说，我们给定的结果最终只有一个类别是1,其他是0，因此对于分类问题，梯度等于：

最后放一份CS231N的代码实现，帮助进一步理解：

   
   
     
    
    
      #coding=utf-8
    
    
      import numpy as np
    
    
      

    
    
      def softmax_loss_native(W, X, y, reg):
    
    
          '''
    
    
          Softmax_loss的暴力实现，利用了for循环
    
    
          输入的维度是D，有C个分类类别，并且我们在有N个例子的batch上进行操作
    
    
          输入:
    
    
          - W: 一个numpy array，形状是(D, C)，代表权重
    
    
          - X: 一个形状为(N, D)为numpy array，代表输入数据
    
    
          - y: 一个形状为(N,)的numpy array，代表类别标签
    
    
          - reg: (float)正则化参数
    
    
          f返回:
    
    
          - 一个浮点数代表Loss
    
    
          - 和W形状一样的梯度
    
    
          '''
    
    
          loss = 0.0
    
    
          dW = np.zeros_like(W) #dW代表W反向传播的梯度
    
    
          num_classes = W.shape[1]
    
    
          num_train = X.shape[0]
    
    
          for i in xrange(num_train):
    
    
              scores = X[i].dot(W)
    
    
              shift_scores = scores - max(scores) #防止数值不稳定
    
    
              loss_i = -shift_scores[y[i]] + np.log(sum(np.exp(shift_scores)))
    
    
              loss += loss_i
    
    
              for j in xrange(num_classes):
    
    
                  softmax_output = np.exp(shift_scores[j]) / sum(np.exp(shift_scores))
    
    
                  if j == y[i]:
    
    
                      dW[:, j] += (-1 + softmax_output) * X[i]
    
    
                  else:
    
    
                      dW[:, j] += softmax_output * X[i]
    
    
          loss /= num_train
    
    
          loss += 0.5 * reg * np.sum(W * W)
    
    
          dW = dW / num_train + reg * W
    
    
          return loss, dW
    
    
      

    
    
      def softmax_loss_vectorized(W, X, y, reg):
    
    
          loss = 0.0
    
    
          dW = np.zeros_like(W)
    
    
          num_class = W.shape[1]
    
    
          num_train = X.shape[0]
    
    
          scores = X.dot(W)
    
    
          shift_scores = scores - np.max(scores, axis=1).reshape(-1, 1)
    
    
          softmax_output  = np.exp(shift_scores) / np.sum(np.exp(shift_scores), axis=1).reshape(-1, 1)
    
    
          loss = -np.sum(np.log(softmax_output[range(num_train), list(y)]))
    
    
          loss /= num_train
    
    
          loss += 0.5 * reg * np.sum(W * W)
    
    
          dS = softmax_output.copy()
    
    
          dS[range(num_train), list(y)] += -1
    
    
          dW = (x.T).dot(dS)
    
    
          dW = dW/num_train + reg*W
    
    
          return loss, dW

总结

这篇文章介绍了近些年来算是非常常用的一些语义分割方面的损失函数，希望可以起到一个抛砖引玉的作用，引发大家对分割中的损失函数进一步思考。当然对于工程派和比赛派来讲，掌握一种新Loss并且应用于自己的项目或者比赛也是不错的。

附录

1. https://www.aiuai.cn/aifarm1159.html

2. Generalized Dice loss代码实现：Generalized dice loss for multi-class segmentation · Issue #9395 · keras-team/keras

3. Lovasz-Softmax Loss代码：bermanmaxim/LovaszSoftmax

推荐阅读

添加极市小助手微信（ID : cvmart2），备注：姓名-学校/公司-图像分割-城市（如：小极-北大-图像分割-深圳），即可申请加入极市图像分割等技术交流群：每月大咖直播分享、真实项目需求对接、求职内推、算法竞赛、干货资讯汇总、与 10000+来自港科大、北大、清华、中科院、CMU、腾讯、百度等名校名企视觉开发者互动交流~