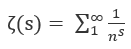花那么多时间去证明它,是否真的值得?
本文来自公众号:超级数学建模
微信号:supermodeling
证明它
到底有什么意义?
你觉得世界上最难的数学猜想是哪个?
我们先来说说下面两个已经被成功解决的猜想:
费马大定理
这个问题是当n为正整数时,找到方程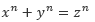
这个猜想是很久以前提出的并且当时费马本人宣称自己能够证明这个猜想,大家还记得当时手边没有草稿纸却又嫌书上空白处太小的费马吗?
费马这一看似任性的行为,引发了长达358年的“费马定理大战”,无数位数学家的内心估计都是一万个草泥马飘过。。。。
而最终真正证明了这个猜想的人是英国数学家安德鲁•怀尔斯(Andrew Wiles),他于1995年在一次讲座里向大家讲述了自己的证明过程。
1995年离现在的我们其实也不算久远,译者家里还有一本藏书是我国著名的数学竞赛教练单墫教授写的《数学竞赛史话》,单墫教授在一开始就介绍了费马猜想,书上写的是费马猜想在当时还没被解决。
当时我就觉得不对劲,费马猜想不是已经光荣地晋升成定理了吗,怎么还没解决呢?后来一看出版日期才明白过来,原来是1990年出版的。霎时心中泛起波澜,数学能发展到今天真的要感谢一代代数学家的辛勤付出啊。
单墫教授的《数学竞赛史话》
第5页
出版日期1990年5月
大家看过辛普森一家吗,里面辛普森的宇宙里就有费马猜想的身影哦,只不过那个反例已经挺接近的了,但不成立!
背后的等号应该是不等号!
庞加莱猜想
庞加莱猜想是美国克雷数学研究所发布的千禧难题中的其中一道。众所周知,千禧难题的奖金是一百万美元。
猜想是这样的:任何一个单连通,闭的三维流形一定同胚于一个三维球面。
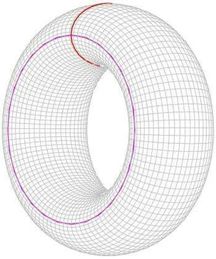
举个形象的例子吧,把一个橡胶圈套在一个物体上,如果我们可以让这个橡胶圈无限缩小成一点,那么这个物体就拓扑同胚于一个球面。
如下图所示,把一个橡胶圈套在一个封闭的甜甜圈上, 无论怎么样, 我们也不能让这个橡胶圈缩到一点去。所以这个像甜甜圈一样的面是不同胚于球面的,这与我们的常识是一致的。
相信大家都知道,庞加莱猜想是7个千禧年难题中唯一一个已经被解决了的问题,而获得这100万美元大奖的便是来自俄罗斯的数学家——格里戈里·佩雷尔曼(Grigory Perelman)。
佩雷尔曼于2002年11月到2003年7月间在网上发布了3篇论文,宣称自己已经证明了庞加莱猜想,并且高冷地表示:
"如果有人对我解决这个问题的方法感兴趣,都在那儿呢,让他们去看吧。我已经发表了我所有的想法,我能提供给公众的就是这些了。"
其实,在此之前,就已经有3位数学家因为对庞加莱猜想证明的推进性研究而获得菲尔兹奖。
1966年,斯梅尔(Smale)因对庞加莱猜想的五维空间和五维以上的证明而获得菲尔兹奖;
1982年,瑟斯顿(Thruston)由于引入几何结构的方法对三维流形进行切割而获得菲尔兹奖;
1983年,福里德曼(Freedman)证明了四维空间的庞加莱猜想,也因此获得了1986年度菲尔兹奖。
不过,快一个世纪以来,人们还是没能将它完全证明出来,所以,这一次佩雷尔曼突如其来的论文,在数学界仍然引起了极大轰动。
接着,克雷数学研究所对佩雷尔曼的证明进行了研究、验证,终于在2005年10月,证实了佩雷尔曼的证明是正确的,并将这3篇论文变成了一个几百页的解析版!
2006年,因庞加莱猜想的证明,国际数学联盟决定将菲尔兹奖颁给佩雷尔曼,然而,佩雷尔曼拒绝了。
2010年,克雷数学研究所将千禧年大奖颁给佩雷尔曼,也同样遭到拒绝。
从此,关于庞加莱猜想证明的探索也终于从历史上完美落幕。

黎曼猜想
这又是一个千禧难题,同样地,如果你解决了,一百万美元就是你的了。
下面是黎曼ζ(zeta)函数的定义:
这里的s可以为复数。我们知道,当s为一个大于1的常数时,该函数对应的级数是收敛的;当s=1是,该函数对应的级数便是我们熟悉的调和级数(harmonic series),它是发散的。
此时,黎曼认为可以通过这个函数的某些性质去近似计算一个给定上限的区间里素数的个数。
(我们经常用素数定理对素数个数进行近似计算,即当x比较大时,小于等于x的素数大约有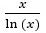
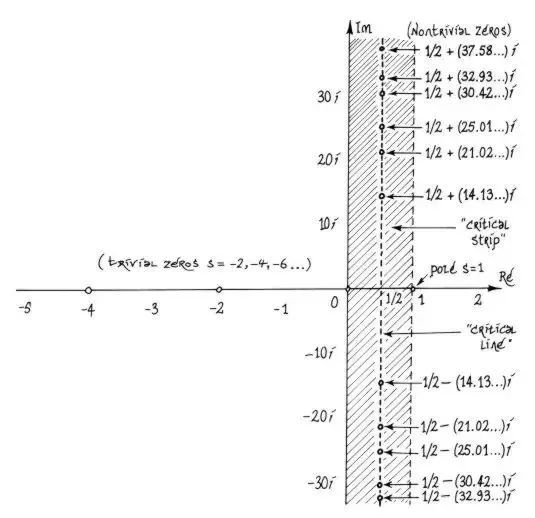
黎曼对素数个数近似计算与上述黎曼ζ函数的零点有关,黎曼已经观察到所有列举出来的非凡零点在复平面内,上面说了s可以为复数,都坐落在x=½这条线上,换句话说就是,这些被列举出来的非凡零点的实部都是½。
但是这仅仅是列举出来的呀,于是经过进一步研究,黎曼猜想,ζ函数所有的非凡零点都坐落在一个带上,如下图所示。
如果可以证明黎曼ζ函数的所有非凡零点都像黎曼所说的那样坐落在图示的带状区域内,那么黎曼猜想就被证明了。
跟其他猜想一样,黎曼猜想的证明之路也是困难重重,不断地有人宣称证明了黎曼猜想,不断被指出其证明有误。
作为当今数学界最重要的猜想,黎曼猜想一旦被证明,其背后跟着的超过1000条数学命题将会晋升为数学定理,期待人类能早日看到那位攀登到顶峰的数学家,是如何给出精彩且完美的证明的。
考拉兹猜想
这真是我最喜欢而又在所有未解决的猜想里最简单的一个了(当然说的是猜想本身的内容
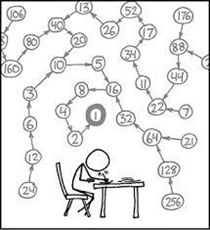
猜想是这样的:对于每一个正整数,如果它是偶数,就把它用2除它;如果是奇数就把它乘3再加1。重复这个过程我们会发现,这最终会进入4—2—1这样一个循环。下图便有一个例子。
下图是对考拉兹猜想的一个抽象,正是这张图片吸引了我。
怎么?不够惊艳?再来看看找到的这张动图。
图片来源: Alex Bellos & Edmund Harriss
不过,对于这个看似非常简单的问题,至今为止,却没人能给出一般情况的证明。
著名数学家保罗·埃尔德什(Paul Erdös)曾说:“数学还没有做好准备面对这样的问题。”
上面那张图就展现了为什么这个问题如此难破解。然而,尽管难破解,还是不断有数学家为之倾尽全力,不计较最后的结果是好是坏。
也许,很多人想问,花那么多时间和精力去证明一个猜想是否真的值得?有什么意义?
在这里,只想说,当然值得!数学符号或数字看起来或许没有什么意义,但不可否认的是,它作为推动人类发展的工具,一直都在发挥着它强大的作用。
人类在证明各种猜想的过程中,先不论这对数学发展的意义是多么的重要,这一过程对人类的思考方式、思维深度、逻辑能力等的发展,绝对是催化剂式的效果。
另外,这难道不正体现了数学的严谨性吗?
数学的公式或定理并不是依赖于猜测,而是需要有严谨的逻辑证明推理过程的,这也使得数学成为了一个解决本学科以及其他学科问题的重要工具。
原文作者:Rahul Ck,伦敦国王学院理论物理理学硕士
译者:正阳小兄弟(内容有增加和删改)
编者:超模君(负责文章内容丰富及润色)
编辑:雾里熊
近期热门文章Top10
↓ 点击标题即可查看 ↓
2. 装物理学家很欢乐很沉重
4. 物理学家辞掉NASA工作玩折纸,竟被请回实验室“折卫星”
10. 我们发现一种『新型炸药』,其原料就在你们刚包好的饺子里 | 正经玩 SP