搞懂 Vision Transformer 原理和代码,看这篇技术综述就够了(十八)

极市导读
本文介绍的2篇文章都是针对如何从Self-attention的内部设计入手,来减小模型的复杂度这一问题。来自UC Berkeley, Google Research的Reformer:高效处理长序列的Transformer以及来自Facebook AI的Linformer: 低秩矩阵逼近实现新的 Self-Attention。>>加入极市CV技术交流群,走在计算机视觉的最前沿
专栏目录
https://zhuanlan.zhihu.com/p/348593638
本文目录
23 Reformer:高效处理长序列的Transformer (ICLR 2020)
(来自UC Berkeley, Google Research)
23.1 Reformer原理分析24 Linformer: 低秩矩阵逼近实现新的 Self-Attention (Arxiv)
(来自Facebook AI)
24.1 Linformer原理分析
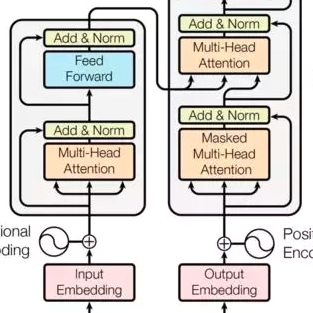
Transformer 是 Google 的团队在 2017 年提出的一种 NLP 经典模型,现在比较火热的 Bert 也是基于 Transformer。Transformer 模型使用了 Self-Attention 机制,不采用 RNN 的顺序结构,使得模型可以并行化训练,而且能够拥有全局信息。
Transformer现在已经成了诸多NLP模型的标配,但是它的问题是,模型太大,不能处理较长的序列。在上篇文章 搞懂 Vision Transformer 原理和代码,看这篇技术综述就够了(六) 中我们提到了2种轻量化Transformer模型的DeFINE,DeLighT。它们分别代表2种轻量化Transformer的方式,即:
-
DeFINE:One-hot vector → word embedding 的过程轻量化。 -
DeLighT:Transformer Block内部轻量化。
它们的共同特点是都是从Transformer结构的外部入手,通过在外部添加一些模块以减少Transformer内部的embedding dimension来减少计算量。但是都没有深入探究如何从Self-attention的角度来减小模型的复杂度。本文介绍的2篇文章就是针对这个问题,即 :如何从Self-attention的内部设计入手,来减小模型的复杂度。
原版Transformer的Self-attention的计算复杂度与序列长度 成平方关系 。而本文介绍的2种方法可以分别把Self-attention的复杂度降低到:
-
Reformer: 。
-
Linformer: 。
23 Reformer:高效处理长序列的Transformer (ICLR 2020)
论文名称:Reformer: The Efficient Transformer
论文地址:
https://arxiv.org/pdf/2001.04451.pdf
23.1 Reformer原理分析:
传统attention的计算方法是:
式中 的维度应为 。所以 的维度是 。假设实验的序列长度是 ,当batch size为1时, 是个 的矩阵,假设使用32 bit存储,也需要16GB的内存。
为了减小内存的使用我们可以每次计算一个 。虽然这种做法不够高效,但是它的内存使用是与序列长度线性相关的。
每一个 token 作为 query 时,要把序列中所有 token 当成 key 去计算注意力,再在所有 token 上加权得到当前 token 的一个表示,但我们知道注意力一般是非常稀疏的,权重就集中于少数几个 token 上,那不如只在这几个 token 上计算权重并加权,这样就大大减少了 self attention 里 的计算量和内存占用量。
也就是说内存耗费的真正原因是要去计算 。而其实我们真正关心的是 。而softmax的取值主要被其中较大的元素主导,因此对 的每个向量 ,只需要关注 中哪个向量最接近 。比如说如果 的长度是 ,对于每个 ,我们只需要关注其中跟 距离最近的32或64个 。
如下图1所示,对于每一个 ,我们只需要找出黑点对应的 即可。
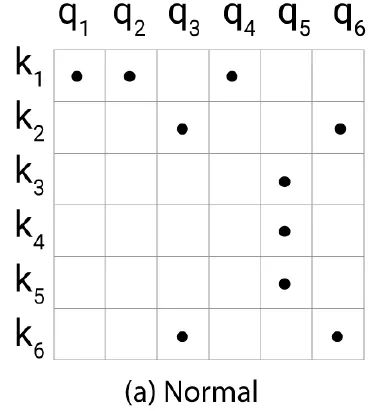
所以现在的问题是:如何找到与每个 这距离最近的这32或64个 ?或者说怎么才知道那少数几个 token 是哪几个?
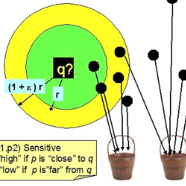
假如要完全靠注意力计算出来才能得到的话,怎么可能在计算注意力之前就知道哪几个 token 权重大? 是不可能,但是在 self attention 里,query 和 key 计算权重,就是简单的内积,和 query 相似的 key 权重大。模型学习到注意力,是指学习到生成正确的 query 以及 key 的表示,在计算注意力时只需要比对 query 和 key 就可以了。- 所以问题转换成,对每一个 query,我先找到相近的几个 key 计算注意力就好了。怎么找?当然不是全部算一遍取 top k,那就与我们减少计算量的初衷相悖,在这里作者用到了 Local Sensitive Hashing (LSH),局部敏感哈希,大意就是相近的向量,映射到同一哈希值的概率较大,多个相近的、映射到同一哈希值的向量相当于装进了同一个桶里 (bucket),那么我们只需要对每个桶里的向量计算 self attention。两个向量 ,满足 LSH 的哈希函数 能做到:

本文通过Locality sensitive hashing来解决这个问题。其特点是对于每个向量 ,在经过哈希函数 后,在原来的空间中挨的近的向量有更大的概率获得相同的哈希值。
这里相关领域已经有很多研究,对于不同的距离度量 ,有不同的 满足 。显然在这里我们的距离度量是 cosine 距离,对应的 哈希是球形投影,即将向量投影到一个 b 维超球面上,该球面被分成了 个象限,投影到同一象限的向量即在同一个桶中,该投影哈希具体写出来是:

式中 是尺寸为 的一个随机矩阵。 是一个 维度的行向量。注意 是个 维的向量作 之后的结果,反映了最终映射到这 个桶中的哪一个。
这个哈希过程就如图2所示:根据queries或者keys的哈希值把它们分到不同的桶里面,在图中 在1号桶, 在2号桶, 在3号桶。

接下来的一个问题是,一个桶里面,query 和 key 的数量不一定相等,比如图2就是这样。而且有可能一个桶里许多 query,没有 key。于是作者干脆 share ,即令 query 和 key 相同,都是 embedding 从同一个线性变换出来的。也就是输入经过线性变换 得到 矩阵,经过线性变换 得到 矩阵,那么 ,如图3所示。只不过 key 做了归一化操作 。
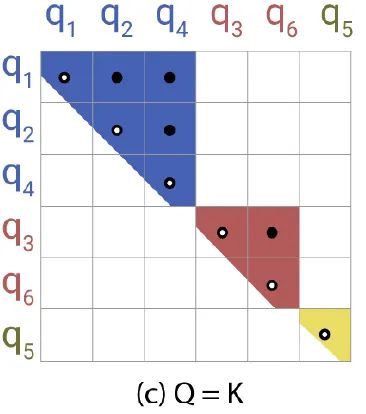
chunk 操作:接下来作者并不是让每个桶里分别做 self attention,而是做了分段,即把同一个桶里的放在一起,重新排成一个序列,然后等长切成若干个段,段内做 self attention,相邻的段也做一次 attention。这里其实有点疑问,论文的图画的非常理想,每个桶的大小差不多,可能差了一两个可以通过相邻段做 attention 来弥补,但是实际情况并不知道每个桶的大小。也许是因为 attention 本身也是学习出来的,作者这么人为设置,是不是相当于给了一个每个桶大小都趋于相同且等于段长的先验限制了 attention 的学习,如下图4所示。

Multi-round LSH attention
lsh 是有概率把距离接近的 分到一组,但也不能完全保证所有距离接近的 分到一组刚好都分到了一组中因为有概率就有误差,因此就多次 hash 来保证概率,取多轮 hash 的并集来保证相似的向量能落到同一个桶里。这里取并集而不是交集,个人理解是桶一多,hash 其实很稀疏,不相似的向量落在同一个桶的概率远小于相似的向量落在不同桶的概率。
Causal masking for shared-QK attention
正常的 transformer 在 decoder 端是要做时序掩码的,这里 lsh 把序列顺序打乱了,因此也要做对应的处理,保证时序掩码的正确性。- 值得一提的是大部分 self attention 的实现,value 包括了自身,但是在 lsh 里不能包含自身,因为 key 和 value 共享值,自身永远是最相似的。
更具体来说可分为以下5个步骤:
-
取 ,令输入序列 。
2. 做LSH bucketing,即进行hash计算,得到每个query和key所归属的桶 (不同颜色表示不同的桶),复杂度 。
3. 根据桶编号对query进行排序,同个桶中,按照query原本的位置进行排序,复杂度 。
4. 对于排序后的新序列,进行 chunk 拆分。
5. 对于每个query只attend自己以及自己之前的chunk,对于这些候选集中相同桶的key进行attend,复杂度 。
式中 为chunk数, 为chunk长度, 。
所以复杂度降为了 。
Reversible Transformer
这一部分的想法来自论文:The Reversible Residual Network: Backpropagation Without Storing Activations,即使用可逆残差网络代替标准残差网络。
这篇论文的出发点是:当前所有的神经网络都采用反向传播的方式来训练,反向传播算法需要存储网络的中间结果来计算梯度,而且其对内存的消耗与网络单元数成正比。这也就意味着,网络越深越广,对内存的消耗越大,这将成为很多应用的瓶颈。由于GPU的显存受限,使得网络结构难以达到最优,因为有些网络结构可能达到上千层的深度。如果采用并行GPU的话,价格既昂贵又比较复杂,同时也不适合个人研究。

上面是torchsummary截图,forward和backward pass size就是需要保存的中间变量大小,可以看出这部分占据了大部分显存。如果不存储中间层结果,那么就可以大幅减少GPU的显存占用,有助于训练更深更广的网络。多伦多大学的Aidan N.Gomez和Mengye Ren提出了可逆残差神经网络,当前层的激活结果可由下一层的结果计算得出,也就是如果我们知道网络层最后的结果,就可以反推前面每一层的中间结果。
这样我们只需要存储网络的参数和最后一层的结果即可,激活结果的存储与网络的深度无关了,将大幅减少显存占用。
实验结果显示,可逆残差网络的表现并没有显著下降,与之前的标准残差网络实验结果基本旗鼓相当。
可逆块结构
可逆神经网络将每一层分割成两部分,通过将 channel 一分为二,做成两路,分别为 和 ,每一个可逆块的输入是 ,输出是 。其结构如下:
正向计算:
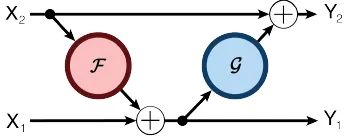

逆向计算:
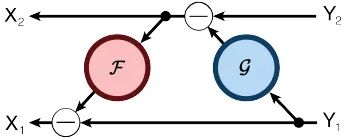

其中 和 都是相似的残差函数,参考残差网络。可逆块的 stride 只能为1,也就是说可逆块必须一个接一个连接,中间不能采用其它网络形式衔接,否则的话就会丢失信息,并且无法可逆计算了,这点与残差块不一样。如果一定要采取跟残差块相似的结构,也就是中间一部分采用普通网络形式衔接,那中间这部分的激活结果就必须显式的存起来。
不用存储激活结果的反向传播
为了更好地计算反向传播的步骤,我们修改一下上述正向计算和逆向计算的公式:
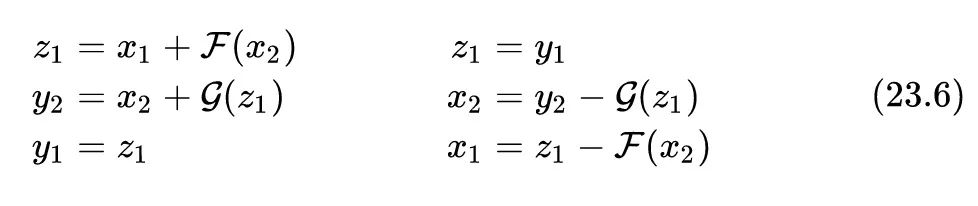
尽管 和 的值是相同的,但是两个变量在图中却代表不同的节点,所以在反向传播中它们的总体导数是不一样的。 的导数包含通过 产生的间接影响,而 的导数却不受 的任何影响。
在反向传播计算流程中,先给出最后一层的激活值 和误差传播的总体导数 ,然后要计算出其输入值 和对应的导数 ,以及残差函数 和 中权重参数的总体导数,求解步骤如下:

计算开销
一个N个连接的神经网络,正向计算的理论加乘开销为N,反向传播求导的理论加乘开销为2N(反向求导包含复合函数求导连乘),而可逆网络多一步需要反向计算输入值的操作,所以理论计算开销为4N (前向N,反向N(反向计算输入值)+2N(反向传播)),比普通网络开销约多出33%左右。但是在实际操作中,正向和反向的计算开销在GPU上差不多,可以都理解为N。那么这样的话,普通网络的整体计算开销为2N,可逆网络的整体开销为3N,也就是多出了约50%。
再回到Reformer中:
Reformer 中把两个函数 和 分别改成了Self-attention和FFN,这样就对应了 transformer 的可逆结构。

可以看到计算 时只用了上一层的激活值 ,计算 时用了上一步计算出来的 ,因此不需要存储这两个激活值。虽然节省了空间,但是激活函数需要重新算一遍,相当于用时间换空间。 原始论文用在 resnet 里,节约显存可以换得更大的 batch_size,在 transformer 中就可以用来训练更长的 sequence。
注意到Transformer的FFN中的hidden dimension 的值也相当大 (约为4K),其依然受序列长度影响,为了减少这一部分显存占用,作者有一次采用了 chunking,因为 FFN 这里是不存在序列依赖的,完全可以拆成几段计算。为了减少这一部分显存占用,作者有一次采用了 chunking,因为 FFN 这里是不存在序列依赖的,完全可以拆成几段计算,又一次用时间换空间。
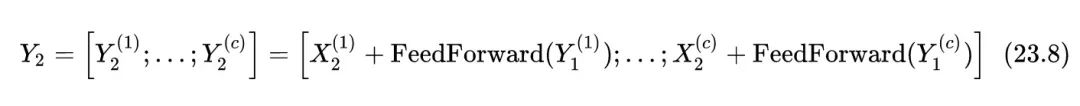
此外,对于词典较大的应用场景,作者在计算损失 log-probabilities 时也是分段的。
作者还额外提到,当使用了chunking和reversible layers以后用于存储激活值的memory use就与layer数无关了。这样节省的是反向传播计算梯度时用到的中间临时变量,并不会节省参数量,节省参数量在 GPU 的消耗可以通过将其转到 CPU 内存来解决,通常这样的操作得不偿失,因为在 CPU 和 GPU 之间传输数据非常耗时。
24 Linformer: 低秩矩阵逼近实现新的 Self-Attention
论文名称: Linformer: Self-Attention with Linear Complexity
论文地址:
https://arxiv.org/pdf/2006.04768.pdf
-
24.1 Linformer 原理分析:
Linformer看重的是Attention内部的轻量化。原版Transformer的Self-attention的计算复杂度与序列长度 成平方关系 。作者的目的是设计一个新的Self-attention机制,使得它的计算复杂度与序列长度 成线性关系 。注意不仅是计算量的下降,参数量也会相应减小。由此产生的线性Transformer,即Linformer,性能与标准变压器模型相当,同时具有更大的内存和时间效率。
Linformer的实现基于这样一个假设,即:self-attention是一个低秩矩阵,更准确地说,self-attention的这个随机矩阵可以用低阶矩阵近似。根据这个假设,就可以把self-attention在空间和时间复杂度降低为 操作。做法是把原来的dot-product attention通过linear projection变成小一点的attention,这些attention形成了原版self-attention的低秩分解。
为了下文叙述的方便我们先统一下attention操作的符号:

式中, 代表input embedding matrices, 为序列长度, 是embedding dimension, 是head的数量,每个head的计算方法是:
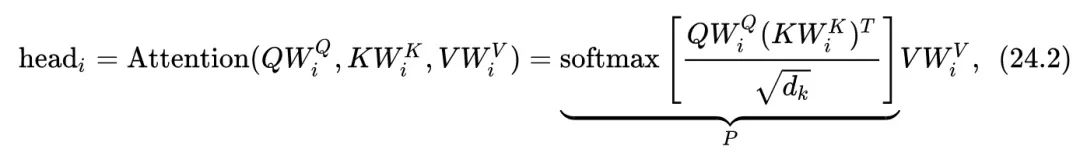
其中, 是attention操作的权重:
,一般来说 。
self-attention就是为了计算上式中的context mapping matrix ,它的计算要把2个 的矩阵作矩阵乘法,其计算复杂度是 。
Self-Attention is Low Rank
回到一开始的假设:为什么self-attention是一个低秩矩阵?
分析2个已有的预训练模型:RoBERTa-base (12层堆叠的Transformer)和RoBERTa-large (24层堆叠的Transformer)。任务是masked-language-modeling task和分类任务,数据集分别是Wiki103和IMDB。作者对模型的不同层、不同注意力头对应的矩阵 ,都进行了谱分解。
谱分解( Spectral decomposition) 又叫做 特征分解 (Eigendecomposition) ,又称谱分解(Spectral decomposition)是将矩阵分解为由其特征值和特征向量表示的矩阵之积的方法。需要注意只有对可对角化矩阵才可以施以特征分解。
可对角化矩阵是线性代数和矩阵论中重要的一类矩阵。如果一个方块矩阵 相似于对角矩阵,也就是说,如果存在一个可逆矩阵 使得 是对角矩阵,则它就被称为可对角化的。
下面是对特征分解的一个简单的介绍,熟悉的读者可以直接跳到图1。
当且仅当下式成立时, 维非零向量 是 矩阵 的特征向量。
其中 为一标量,称为 对应的特征值。也称 为特征值 对应的特征向量。在一定条件下(如其矩阵形式为实对称矩阵的线性变换),一个变换可以由其特征值和特征向量完全表述,也就是说:所有的特征向量组成了这向量空间的一组基底。为了求出特征值,令
显然,这个方程是一个齐次线性方程组。
有非零解的充分必要条件是 ,即 。
所以求特征值和特征向量的过程转化为了求 的解的过程,而这个式子也叫做矩阵 的特征方程, 是关于 的 次多项式,称为矩阵 的特征多项式。由代数基本定理,特征方程有 个解。这些解的解集也就是特征值的集合,有时也称为 “谱”(Spectrum) 。对 进行因式分解,可以得到:
其中, 。对每一个特征值 ,我们有下式成立:
对每一个特征方程,都会有 个线性无关的解。这 个向量与一个特征值 相对应。这里,整数 称为特征值 的几何重数,而整数 称为特征值 的d代数重数。这里需要注意的是几何重数与代数重数可以相等,但也可以不相等。一种最简单的情况是 。
矩阵的特征分解
令 是一个 的方阵,且有 个线性无关的特征向量。这样, 可以被分解为:
其中 是一个 的方阵,且其第 列为 的特征向量。 是对角矩阵,其对角线上的元素为对应的特征值 。这里需要注意只有可对角化矩阵才可以作特征分解。
若矩阵 可被特征分解并特征值中不含零,则矩阵 为非奇异矩阵,且其逆矩阵可以由下式给出:
对特殊矩阵的特征分解
对称矩阵
任意的 实对称矩阵都有 个线性无关的特征向量。并且这些特征向量都可以正交单位化而得到一组正交且模为1的向量。故实对称矩阵 可被分解成:
其中 为正交矩阵, 为实对角矩阵。
上面是对矩阵的谱分解 的一些简要的介绍。
图1的左边2个图是分别把模型RoBERTa-base和RoBERTa-large 在 Wiki103 和 IMDB 这2个数据集上得到的各个 layer 的各个 head 的 attention 矩阵做类似的谱分解。之后把得到的 的奇异值进行累加,再进行归一化,得到一堆数,这些数的和为1因为经过了归一化过程。假设某个 ,那么这512个归一化之后的数进行从左到右的累加,最右边的数一定累加到了1。再之后就把归一化值的累加结果称之为Normalized cumulative eigenvalue,也就是图1左侧2幅图的纵轴代表的含义。从结果来看,无论是12层的模型RoBERTa-base还是24层的模型RoBERTa-large,曲线都呈一条长尾分布,也就是说,累加值很快就会上涨到接近1的位置,而后面大量的奇异值都是较小的数值,这说明:矩阵 中的大部分信息都可以由少量最大的奇异值来恢复。
图1最右侧的图是在 Wiki103 这个数据集上的不同layer,不同head的某一个值的热图 (heatmap),这个值是上文介绍的512个归一化值的累加结果中的排名第128大的这个累加值。它反映了在这512个归一化的特征值中,我们把前128大的这些特征值加在一起的结果。可以看出,在layer index较小时,也就是在网络的浅层,这个值就可以达到0.86左右;而在网络的深层,这个值就可以达到0.96左右,证明更高层的 Transformers 中,会比更低层的 Transformers 有更大的偏度。这意味着,在更高层,更多信息集中在少量最大的奇异值中,且矩阵 的秩是更低的。

上面是对模型相关数据的统计结果,作者还给出了对谱分解结果的相关理论分析。
所以就自然引出了一个问题:能不能把 的矩阵 替换成一个低秩矩阵 ,而且误差不太大呢?
Theorem 1. (self-attention is low rank) 对于任意的 和 ,对矩阵 中的任意的一个列向量 ,都存在一个低秩矩阵 满足:
式中 的定义如19.2式所示。
先解释下上面这个Theorem 是啥含义,再给出证明。
大于号左边的 是这个模型的attention map,就是 和 相乘得到的 矩阵。 是用来模仿,或者说用来代替 的一个低秩矩阵。
那这个 究竟能不能起到和 一样的效果呢?要验证这件事情,就要看它和 相乘之后的结果是否有很大的不同。这里我们取 里面的任意一个向量 ,那么现在要比较的就是 和 的差距到底有多大。这个Theorem 告诉我们,这个差距小于 的概率是接近1的。而且,这个低秩矩阵 的秩是: 。
证明:
根据上式 (19.2) 有:
为什么可以写成这个形式,举个例子:
这里和原论文的 有一点出入,但并不影响证明。
把 表示成这个形式以后,接下来要应用一个叫做Johnson–Lindenstrauss lemma的定理。
lemma 1. 假设 是个 的矩阵, ,其中的值服从 的独立同分布。对于任意的 ,有:
假设:
式中, 是 的矩阵, ,其中的值服从 的独立同分布,有:
假设任意的行向量 ,任意的列向量 ,根据上面的JL Lemma,有:
所以:
(a)这一步怎么来的?
the union bound一致限: 讲的是:对于任意2个事件 我们有:
所以
所以
所以
(b)这一步是把 带进去。
我们如果把 取为 ,则上式最终变为:
得证。
有了上面的结论以后,接下来的问题是:如何得到这个低秩矩阵 ?
一种直观的想法是把 进行奇异值分解以后,对它的前 个奇异值进行操作:
式中, 代表第 大的奇异值和奇异向量。
如果我们使用 来代替self-attention中的 这个矩阵,其误差将会是 ,计算复杂度为: 。但是另外的一个问题是SVD分解也是需要计算复杂度的,所以作者通过另外的手段来的得到这个低秩矩阵。
Linformer的具体做法如下图2所示:
linear self-attention在计算key和value之前加入了2个线性层,以线性空间和时间复杂度计算矩阵 。其核心思想是,用两个线性投射矩阵 来计算 矩阵。
这样, 矩阵由原来的 变为了 ,attention map 由原来的 变为了 的矩阵 。写成公式为:

这一过程的计算过程的复杂度为 ,其中, ,且不会随着序列长度 的变化而变化,我们可以显著降低时间和空间的消耗。以下定理我们将证明,当 时,我们可以在 的误差范围内,近似 。

按照上面的做法有 ,还是与 呈正相关,那么 能不能取得再小一点,使之与 独立呢?
所以有下面的这个Theorem 2。
Theorem 2. (Linear self-attention) 对于任意的 和 ,如果 ,则存在矩阵 使得对于 矩阵 中的任意行向量 有:
先解释下上面这个Theorem 是啥含义,再给出证明。
原版Transformer的计算方法是把attention矩阵 中的每个向量 都与 相乘,现在是把这个向量 先进行线性变换 ,再与同样经过线性变换 的 相乘。那这2种办法的结果差值是:
我们要证明的是这个差距足够的小。
证明:
定义 。假设 是个 的矩阵, ,其中的值服从 的独立同分布。 是个常数,且 ,我们首先证明的是对于矩阵 中的任意行向量 和矩阵 中的任意列向量 ,有:

根据三角不等式有:
(a)这一步 先使用柯西不等式变成:
根据lemma 1.1有:
(b)这一步使用了Lipchitz continuous in a compact region。
(c)这一步利用了lemma 1.2,也正是这一步引入了不等式右侧的 。
至此我们证明了20.4的成立。注意式20.4中的 是任意的行向量,将其替换成attention矩阵的行向量 ,如果取 则有下式成立:

但是这种情况的前提是你取了 ,那这样一来矩阵 的秩就还是与 有关了。在这种情况下Self-attention的计算复杂度是:
还是没有缩减到线性。
至此,作者又给出了一种假设,即取 那这样一来矩阵 的秩就还是与 有关了。在这种情况下Self-attention的计算复杂度与 线性相关:
作者要证明能找到这样一个矩阵 使之依旧满足19.5式:

证明:
定义矩阵 :
对于矩阵 的任意一个行向量 ,有:
注意式中 由原来的 缩减为 。
(a)这一步利用了不等式 ,式中 。
(b)这一步利用了谱范数小于任何一种矩阵范数 。
(c)这一步利用了式19.5的结论。
Theorem 2说明了下图3,即:
在计算key和value之前加入了2个线性层,使得 矩阵变为了 ,这样attention矩阵的维度就由原来的 变成了 。这就实现了用一个 矩阵来代替原来的 矩阵的效果,且计算复杂度变成了 ,与 成线性关系。

除此之外,Linformer 还使用了其它的一些提升表现和效率的技巧。
参数共享 我们实验了三种层级的参数共享。
-
Headwise: 所有注意力头共享 和 参数。 。 -
Key-Value: 键值参数共享。对于每一层,所有的注意力头的 的 Projection矩阵共享参数同一参数, 。 -
Layerwise: 所有层参数共享。对于所有层,都共享投射矩阵 。
一个12层,12个头的 Transformers 模型,在分别用上述参数共享后,其参数矩阵的个数分别为 24,12,和 1。
适应性的投影维度 因为注意力矩阵是低秩的,我们可以动态调整 的大小,让更高层的 Transformers 选用更小的 。
其它投影方法 除了用两个矩阵线性近似,还可以用均值/最大池化,或卷积的方式来近似。
Experiment:
模型用的 RoBERTa 的架构,语料用了 BookCorpus 和 英文的维基百科,大约 3300M 单词的预训练语料。所有实验模型的训练目标都是 MLM,在 64 张 Tesla V100 GPUs 上训练了 250k 的迭代。
实验验证了3个问题:
-
Projected dimension的影响:
如下图所示为Projected dimension的影响。左右2图分别是序列长度 为512或者1024的情况。随着 的增大,Linformer的性能越来越好。有趣的是,当序列长度 为512时, 取128即可与原Transformer的性能相似;当序列长度 为1024时, 取256即可与原Transformer的性能相似。

-
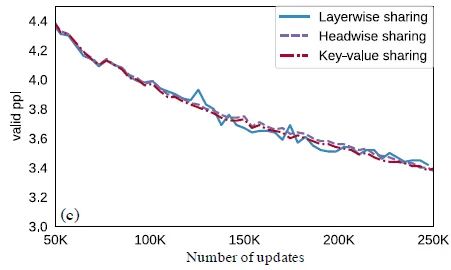
参数共享策略的影响:
作者比较了3种参数共享策略headwise, key-value, layerwise的影响,如下图所示。图中 。结果发现每一层,每个head的2个Project matrix全部共享参数时与不共享的结果差不多。这意味着我们可以通过全局共享Project matrix参数的方法来大量减少参数量。
-
序列长度变化的影响:
如果复杂度是线性的,在 k 值固定的情况下,序列增加,其消耗的时间和空间也应该是线性增长。作者在序列长度分别为 的情况下都取 ,发现最终的性能十分相似,这也反映了Linformer的有效性。

总结:
本文讲解了2种Transformer模型:Reformer,Linformer。它们的目的都是降低self-attention层的计算复杂度。
-
Reformer: -
Linformer: 通过Projection matrix,把 的attention map强制转换成 的,实现了计算复杂度 。
这2个模型提供了2种压缩Transformer模型的维度。
参考:
https://thinkwee.top/2020/02/07/reformer/
https://posts.careerengine.us/p/5e2c68210e43925a122123ce
如果觉得有用,就请分享到朋友圈吧!
公众号后台回复“88”获取严彬:STARK-
基于时空Transformer的视觉目标跟踪PPT下载

# 极市平台签约作者#
科技猛兽
知乎:科技猛兽
清华大学自动化系19级硕士
研究领域:AI边缘计算 (Efficient AI with Tiny Resource):专注模型压缩,搜索,量化,加速,加法网络,以及它们与其他任务的结合,更好地服务于端侧设备。
作品精选