概率质量函数与累积分布函数(离散) - 图解概率 03

概率质量函数与累积分布函数-离散

随机变量

随机变量其实就是函数, 将各种事件映射成对应的数字.

比如将抛一枚公平的硬币正面(国徽/人头)指定为 1, 反面(数字/尾)指定为 0. X(硬币正面)=1, X(硬币反面)=0.

再比如掷骰子点数对应成相应的数字 1~6. X(点数1)=1, X(点数2)=2, ......, X(点数6)=6.

注意: 随机变量的函数也是一个随机变量. 

概率质量函数与累积分布函数

概率质量函数(Probability Mass Function, PMF)表示随机变量相应每个数字代表的概率. 以掷骰子为例, P(X=1)=1/6, P(X=2)=1/6, ......, P(X=6)=1/6.

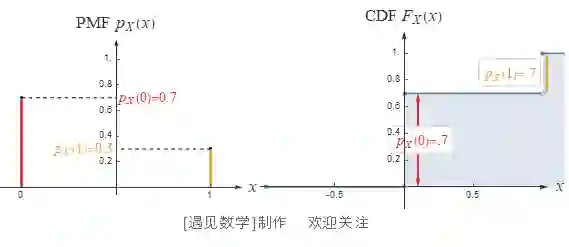
累积分布函数(Cumulative Distribution Function, CDF) 是 X ≤ x 的概率, 即 P(X≤x) . 两者的关系以伯努利分布为例观察下图:

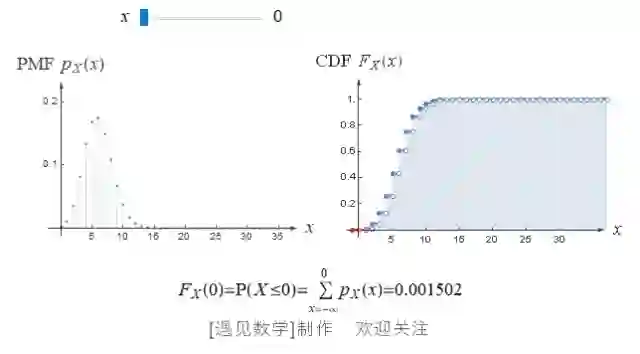
如已经知道了 PMF, 就可以计算出相应的 CDF, 也即将小于等于 x 的概率相加, 观察下面动图:

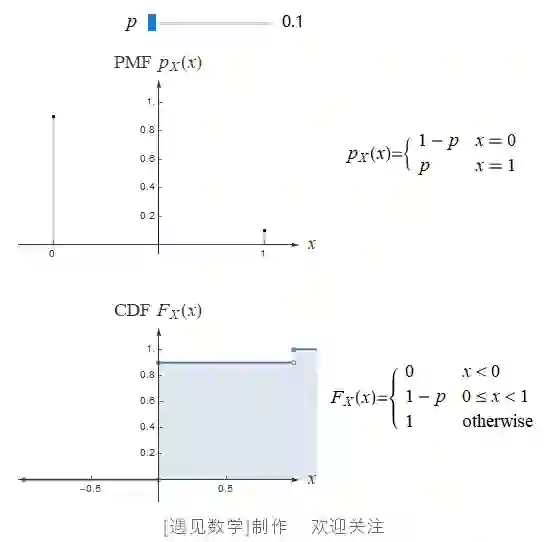
伯努利分布(Bernoulli Distribution , 也称0-1分布)

每次试验只有成功1和失败0两种, 成功概率 p, 失败概率则为 1-p.

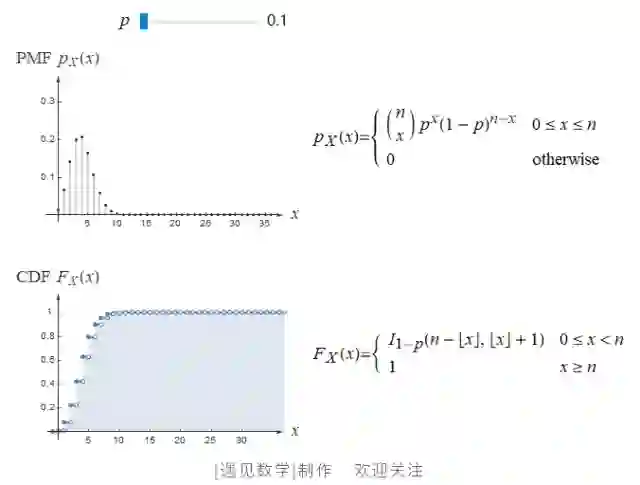
二项分布(Binomial Distribution)

进行了 n 次的伯努利试验, 恰好成功了 x 次.

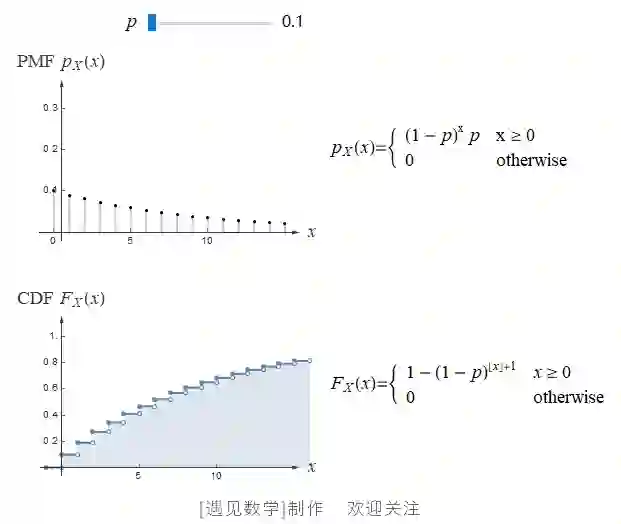
几何分布(Geometric Distribution)

进行了一系列伯努利试验, 获得首次成功的是第 x 次试验, 则该随机变量满足几何分布.

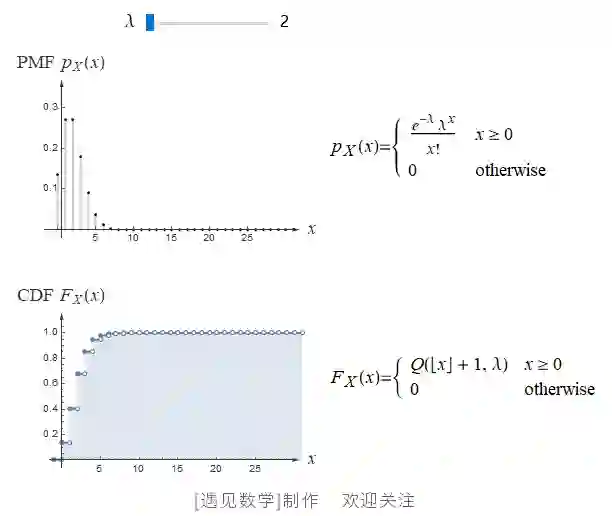
泊松分布(Poisson Distribution)

单位时间内随机事件发生的次数的概率分布, 比如某一服务设施在一定时间内受到的服务请求的次数，电话交换机接到呼叫的次数、汽车站台的候客人数、机器出现的故障数.