从上到下，一文带你看全所有GNN分类

2020 年 8 月 7 日 图与推荐

↑公众号关注 Graph-AI

专注于 图网络与机器学习

文 · 成森封面 · pixabay

从上到下，一文带你看全所有GNN分类

一般来说，我喜欢 从上往下 的角度来入门一个方向，毕竟入门的秘诀就是 从广到深 ，而不至于在一开始就只见枝叶不见森林。先在心中有个谱，然后再慢慢奏好每个音符，这样就会出来美妙的旋律。

这个系列挑选了清华大学刘知远老师的《 Introduction to Graph Neural Networks 》和他们的一份综述《 Graph Neural Networks: A Review of Methods and Applications 》作为参考。优秀的综述很多，我可能也参考了其他，但主要还是这两者。

本文是一个序章，是一篇导读文，从本文开始，后面的文章我再细细拆分和详解。

让我们开始吧。

总架构

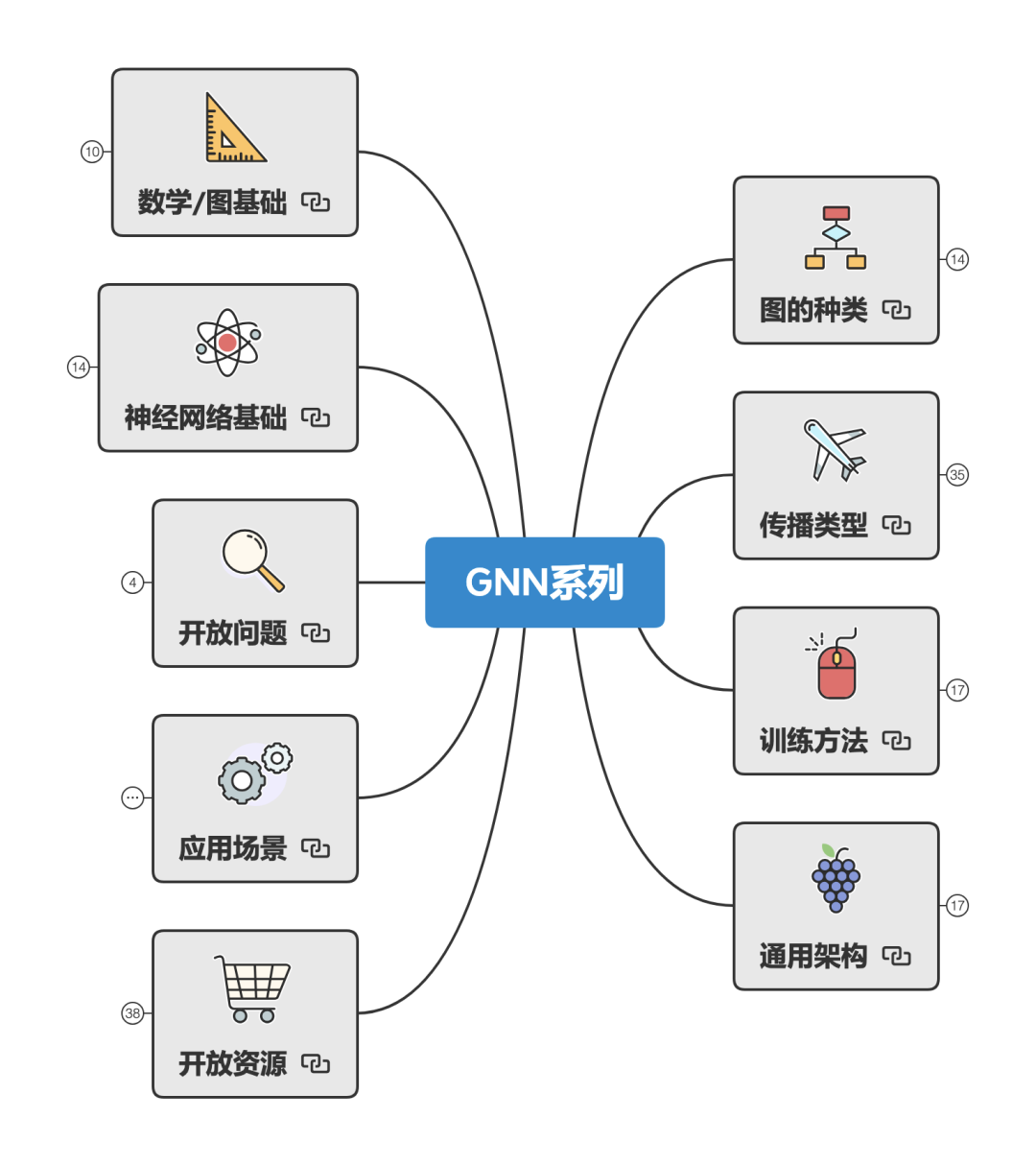
首先是总架构，从下方的思维导图可以看到，我们可以从九个方面来全方面了解我们的GNN。

简单来说可以分成五大部分：

基础：包括理解GNN需要的数学基础、图论基础，和神经网络基础。
GNN的了解 ：包括图的种类、传播类型、训练方法、通用框架。
应用场景 ：GNN在各个场景下的应用。
开放问题 ：探讨GNN的发展方向。
开放资源 ：GNN常用的数据集和代码框架。

从这里开始，我就逐块介绍每一部分。

数学/图基础

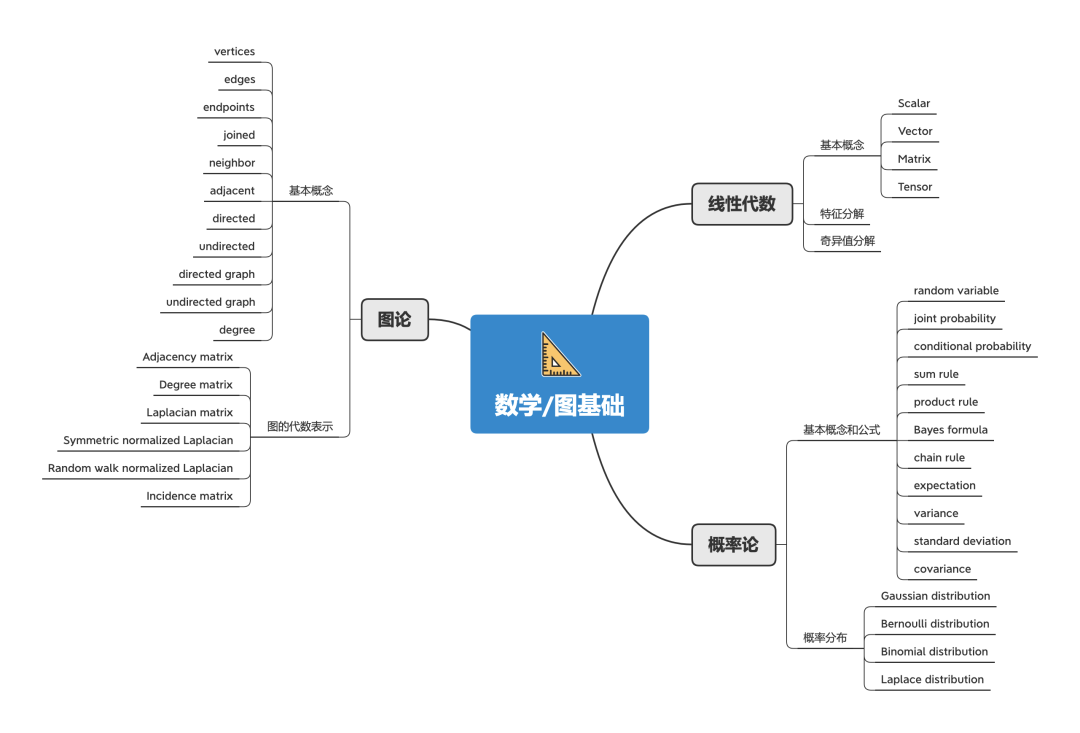
一切深度学习都离不开数学，图神经网络也不例外。为了更方便地理解GNN，这里给出一些相关的数学概念。

线性代数 ：在计算机科学、机器学习领域，线性代数广泛使用。想要对机器学习有深入的理解，就必须对线性代数有个透彻的了解。
概率论 ：不确定性在机器学习领域无处不在，所以我们需要使用概率论来量化和处理不确定性。
图论：图是GNN的基础（这不是废话吗），所以想对GNN有个全面的了解，基本的图论知识是必须的。

神经网络基础

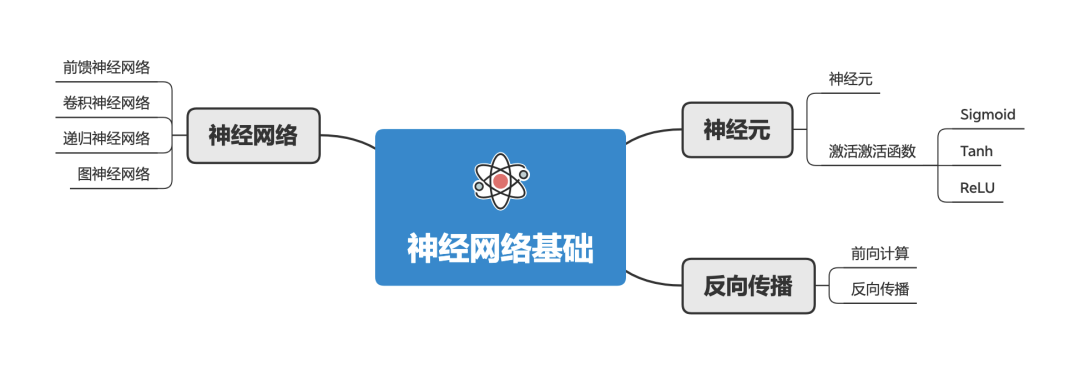
神经网络是机器学习中一个最重要的模型。和人的大脑相似，人工神经网络的结构由许多相互连接的 神经元 组成。

神经网络的训练（学习），一般步骤是：

从随机权重开始；
通过 反向传播 算法反复更新其权重；
直到模型的性能达到目标精度为止。

最终，训练好的神经网络模型把“学来知识”以数字化形式存储到这些神经元的连接中。

很多学者试图改变神经网络的学习方式（不同的算法或结构），来获得更通用的神经网络模型。

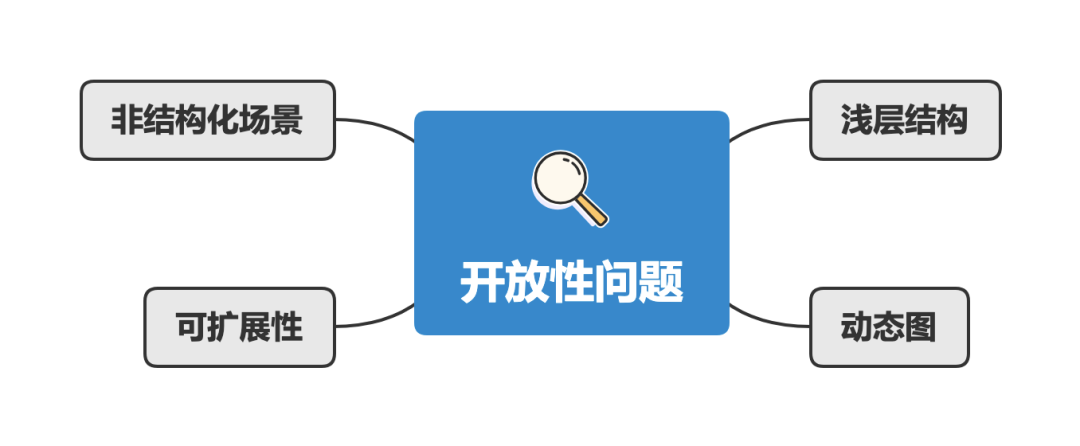
开放性问题

虽然GNN已经在很多领域获得了巨大成功，但GNN还是一些情况下无法提供满意的解决方案。

所以在这里会列出一些开放性问题的方向：

浅层结构 ：神经网络之所以能够获得很好的性能，一个原因在于其可以堆叠更多网络层，使用更多的参数来学习；但是图神经网络却总能只有几层结构，比如深层GCN会导致过平滑问题（就是所有的节点都是差不多的值）。虽然已经有DeepGCN这样的模型，但是更深的GNN仍然是一个已知的挑战。
动态图 ：静态图是稳定的，所以我们可以对其进行建模；但是动态图引进了结构变化。当节点/边动态地出现或消失，但GNN并不能很好的处理。相关的研究仍在进行，相信这会成为通用GNN的稳定性、可扩展性的里程碑。
非结构化场景 ：虽然已经有GNN应用在非结构化场景中，但并没有很好的方法来从原始数据中生成通用图。因此找到更好的图生成方式，能够使得GNN的适用领域更加广泛。
可扩展性 ：如何把图嵌入算法应用在大规模网络（社交网络、推荐系统）中是一个难题，GNN也不例外。GNN的扩展性是一个待解决的问题，因为很多GNN的核心算子都需要耗费大量的计算资源。比如说：

（1）图数据不是规范的欧几里得数据，每个节点都有它自己的不一样邻接节点，所以batches的方式并不适用；

（2）当有数百万个节点和边时，计算图拉普拉斯算子也很困难。

一个算法的可扩展性决定了这个算法是否可以应用在实际生产中。

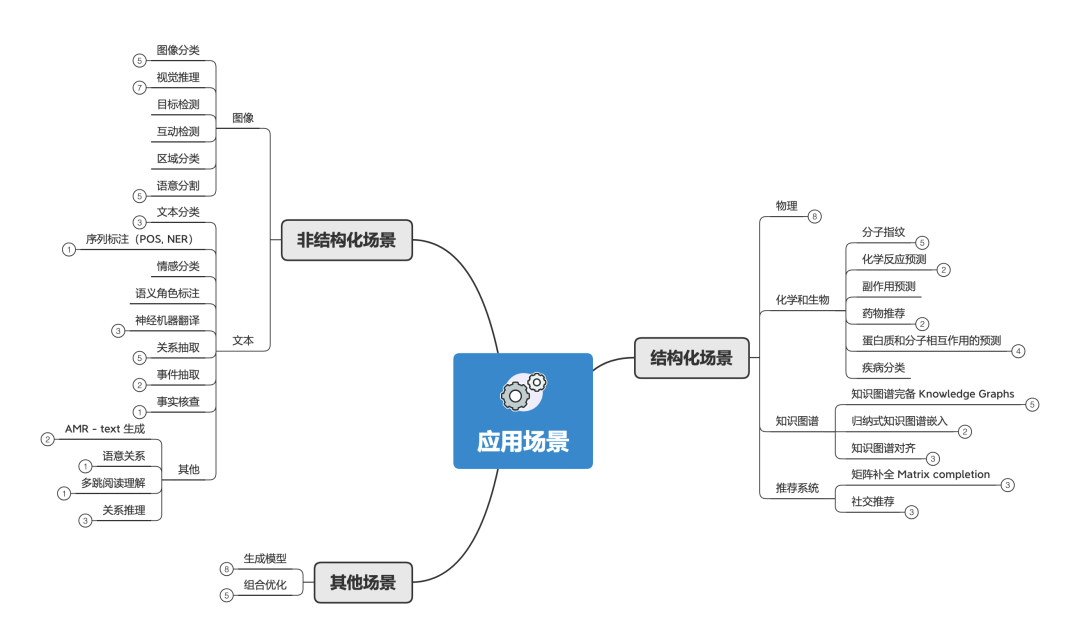
应用场景

在这里，给大家展示GCN应用的几个场景。其中：

结构化场景 ：数据是天然的图，数据之间有明确的关系结构，比如说物理系统、分子结构、知识图谱等。
非结构化场景 ：数据没有明确的关系结构，比如说图像、文本。一般来说有两种方式来把GNN应用在非结构化场景。

整合其他领域的结构化信息来提高性能。比如使用知识图谱的信息来增强图像的 zero-shot 问题；
先推断或者假设非结构化场景中的关系结构，然后用GNN来解决相关问题。比如把文本变成图。

其他场景 ：除了上面两者，还有很重要的GNN应用场景，比如说图生成模型、图的组合优化等。

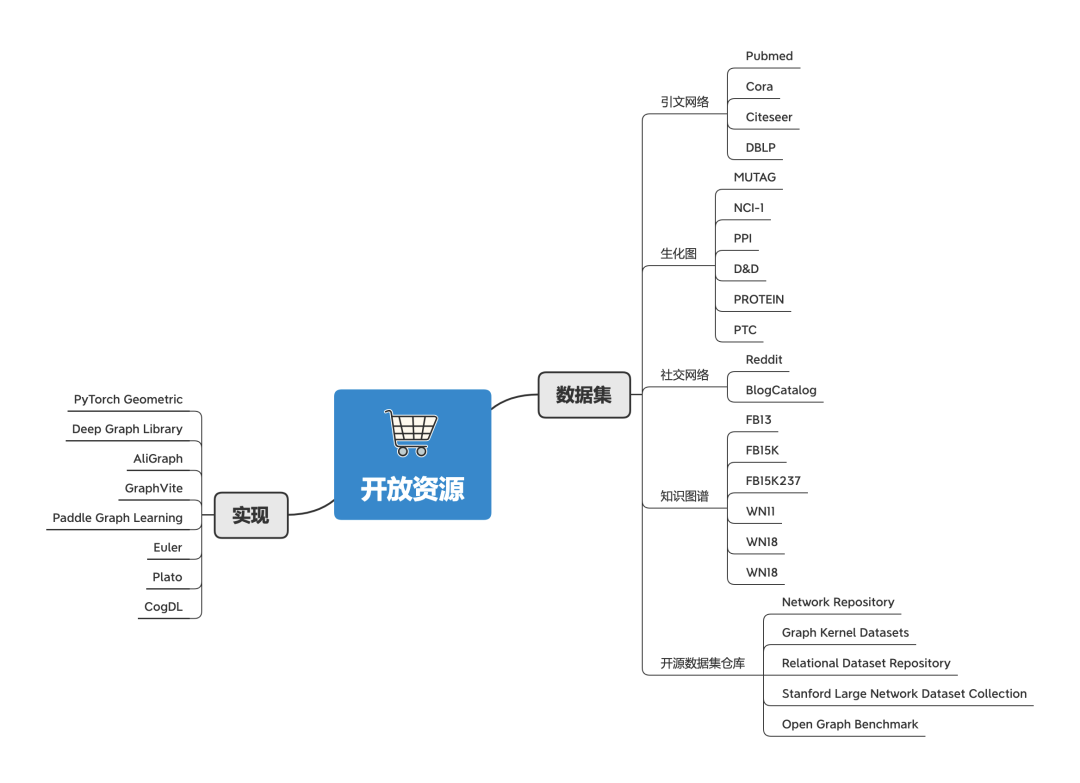
开放资源

很多学者和机构发布了许多与图相关的任务，以测试各种GNN的性能。这些任务一般都会提供数据集。所以按照任务分类，可以把数据集分成以下几类：

引文网络
生化图
社交网络
知识图谱
开源数据集仓库

图的种类

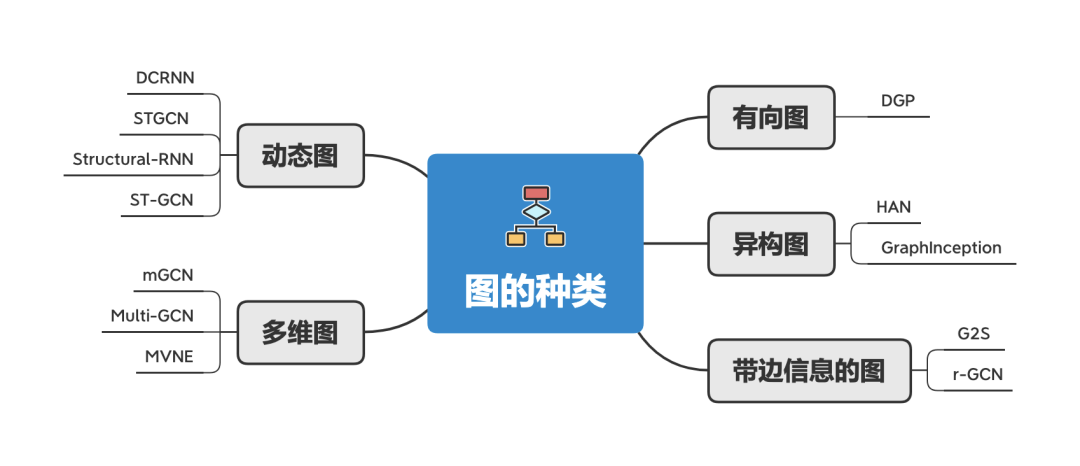
原始GNN是应用在带标签信息的节点和无向边的图上，这是最简单的图结构。但是世界上有很多不同种类的图，而这就要求不同的GNN来处理。

这里介绍几种不同种类的图：

有向图 ：无向边可以当作节点中存在两个有向边。但有向边能够比无向边带来更多的信息。比如说知识图谱中就用到了有向边，来确定父项和子项。
异构图 ：异构图是指存在几种不同类型的节点。处理异构图最简单的方法是把节点的类型视为节点特征的一部分，拼接到节点原有的特征上。
带边信息的图 ：这一类图的边会有额外的信息，这一类图有两种处理方式：

把这类图拆分成二部图，带信息的边变成带信息的节点，最终变成：开始节点-边节点-结束节点。
对于不同类型的边采用不同的权重矩阵来处理。

动态图 ：动态图同时处理静态图结构和动态输入信号。有两种处理方法：

DCRNN、STGCN等工作先用GNN处理图的空间信息，然后输出到 seq2seq 模型或者CNN模型来进一步处理。
Structural-RNN 和 ST-GCN 同时处理图的空间信息和时序信息。他们把时序关系当成一种静态边，转化成静态图，这样就能用传统的GNN来处理。

多维图 ：多维图指的是节点之间有多种关系。形成一个多维度的图（或者叫多视角图、multi-graph）。而这多种关系并没有明确说是互相独立的，所以直接用“一维图”来处理是不恰当的。

多维图的早期工作主要集中于社区检测和聚类。最近工作则采用改良过的GCN、或者把多维图降维到一维图、或者把节点嵌入算法扩展到多维图中来处理多维图。

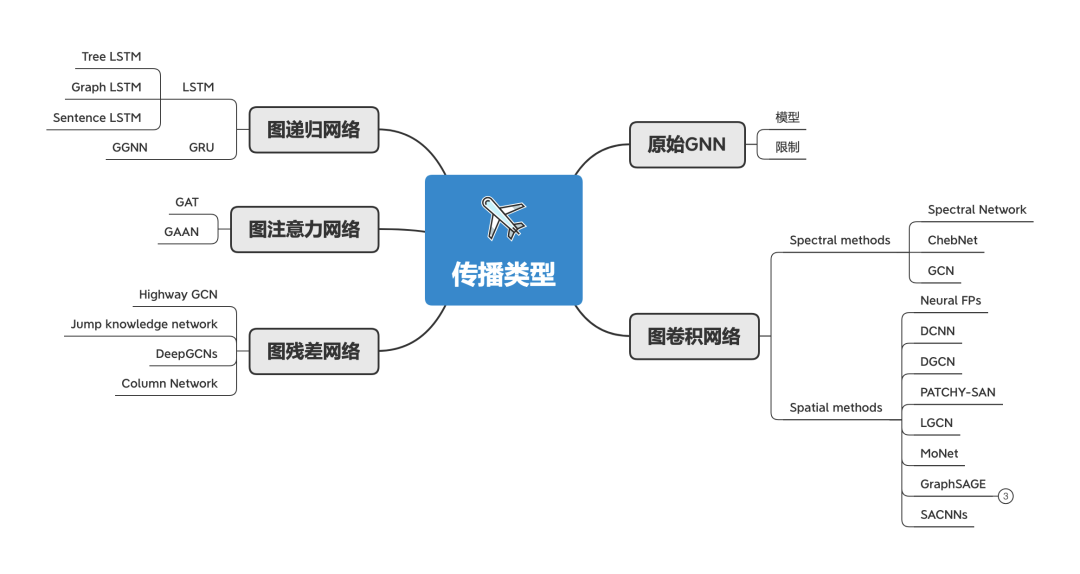
传播类型

GNN的概念是从2004年开始的，为了简单，我们讨论的模型从2009年Scarselli的那篇论文《The graph neural network model》开始，这是一个扩展已有的神经网络来处理图数据的方法。原始GNN指的是这篇论文的图神经网络。虽然原始GNN很强大，但依然有很大的限制：

计算效率低 。需要不断迭代更新节点隐藏层来获得不动点（the fixed point），而这一过程计算效率不高。
学习能力受限 。原始GNN在迭代中共享同一参数，而大多数的神经网络在不同层使用不同的参数。
难以编码边上的信息 。原始GNN并不能很好处理边上的信息，比如说知识图谱中多种类型的边。
有不能区分节点的情况 。如果我们想要节点特征而不是图特征，如果在迭代次数过多的情况就不适合使用不动点（The fixed points），因为不动点的特征分布会变得过于平滑而没法很好地区分每个节点。

The fixed point，不动点、固定点。来自巴拿赫不动点定理(Banach's Fixed Point Theorem)。

从原始GNN开始，衍生了图卷积网络、图递归网络、图注意力网络、图残差网络等。

图卷积网络 ：旨在将卷积推广到图域。在这个方向上的进展通常被归类为 spectral方法和 spatial方法。
图递归网络 ：把RNN的门控机制应用在节点传播上，以突破原始GNN的一些限制，提高图上长距离信息的传播效率。
图注意力网络 ：注意力机制，会为当前节点每一个邻接节点分配不同的注意力分数，以识别更重要的邻接节点。
图残差网络 ：使用skip connections来解决超过3层的图卷积层会引入噪音导致效果反而会变差的问题。

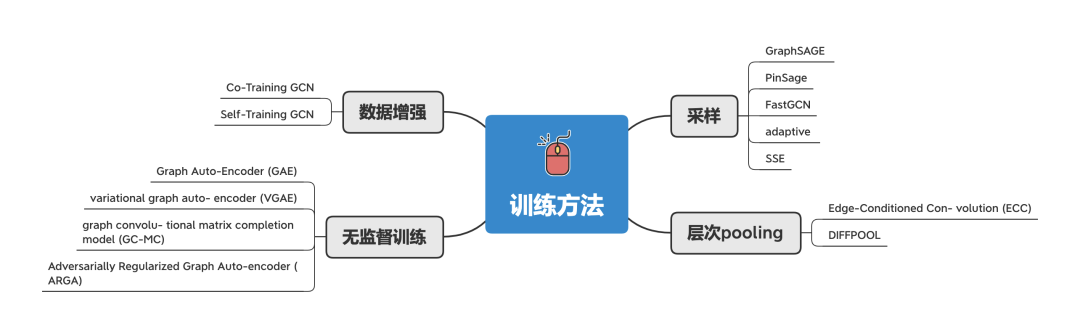
训练方法

由于原始GNN在训练和优化方面存在一些缺陷，所以就衍生了多种训练方法：

采样方法 ：通过对邻接节点进行采样，以减轻训练成本。
层次pooling ：对大型图来说，一般会有丰富的层次结构信息，会对节点/图级别的分类有提升效果。通过类似计算机视觉的pooling的方法，来获得更丰富/通用的特征。
无监督训练 ：把自动编码器（Auto-Encoder, AE）引入到图域上，用来无监督地训练获得低维度的节点特征。
数据增强 ：通过 Co-Training 和 Self-Training 的方法来扩大训练数据集，以改善卷积核局部性缺陷和标签数据不足的问题。

Co-Training 方法可以找到训练数据中的最近节点。
Self-Training 方法则类似于 boosting算法。

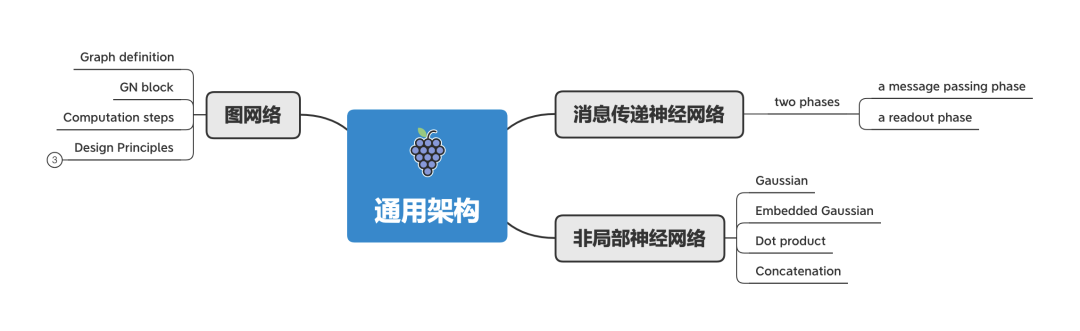
通用架构

除了不同种类的GNN模型外，几个通用框架的提出，将不同类型的模型整合到一个框架中。比如：

信息传递神经网络 ：Message Passing Neural Network(MPNN) 定义了一个统一框架，概括了几种 GNN 和 GCN 方法；
非局部神经网络 ：Non-Local Neural Network(NLNN) 是用来解决计算机视觉任务的，概括了几种自注意力方法；
图网络 ：Graph Network (GN)的提出，则统一了MPNN和NLNN及其变体（Interaction Networks、Neural Physics Engine、CommNet、structure2vec、GGNN、Relation Network、Deep Sets、Point Net）