多模态为什么比单模态好？第一份严谨证明来了！

文 | 橙橙子

面试官: 听说你对多模态感兴趣，请问为什么多模态学习要比单模态学习效果好？
候选人: 直观地，多模态学习可以聚合多源数据的信息，使得模型学习到的表示更加完备。以视频分类为例，同时使用字幕标题等文本信息、音频信息和视觉信息的多模态模型要显著好于只使用任意一种信息的单模态模型，这已经被多篇文章实验验证过。
面试官: 直觉+实验是老生常谈了，我听过很多次了，有没有更严谨一些的证明？
（候选人内心语：面试官这是要找茬呀，还好有萌屋救我...）
候选人：刚好最近看了一篇多模态学习理论分析的文章，从数学角度证明了潜表征空间质量直接决定了多模态学习模型的效果。而在充足的训练数据下，模态的种类越丰富，表征空间的估计越精确，容我细细道来...

论文标题：
What Makes Multimodal Learning Better than Single (Provably)

论文链接：
https://arxiv.org/pdf/2106.04538.pdf

背景

尽管在实际应用中，使用多模态学习构建识别或检测系统经常可以有更好的表现。但是从理论角度讲，我们对多模态学习的认识却极其有限。基础的问题悬而未决：多模态学习能证明比单模态学习效果好么？

在这篇文章中，作者从两个角度回答了这个问题：

1. （When）在何种条件下，多模态学习比单模态学习好
2. （Why）是什么造成了其效果的提升

公式化定义

本文基于一种经典的多模态学习框架，即无缝进行潜空间学习（Latent Space Learning）与任务层学习（Task-specific Learning）。具体地，首先将异构数据编码到一个统一潜空间 ，对应的映射函数族为 ，要寻找的最优的映射是 。接着，潜空间的表示再经过任务层的映射被用于指定任务中，映射的函数族为 ，其中最优映射为 。

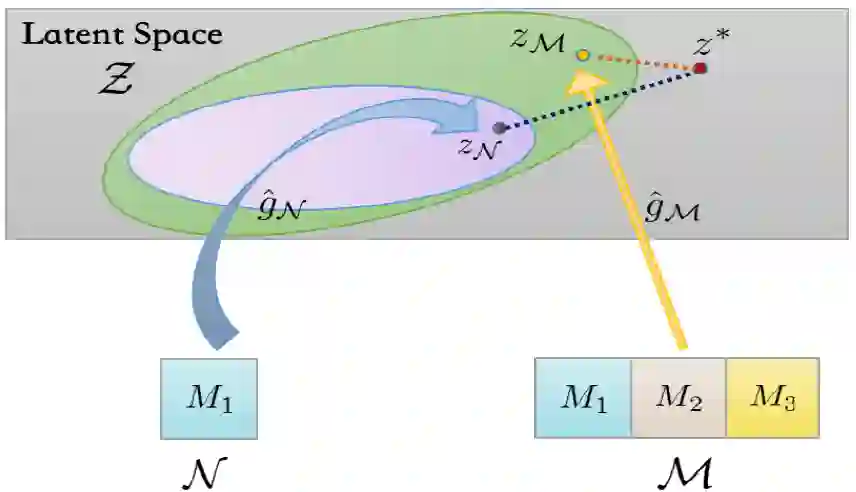
具体地，我们假设共包含有 个模态，其中训练数据 定义为 ，其中 表示第 个模态的信息。输入空间为 ，目标为 。 表示从输入空间（包含所有 个模态）到潜表示空间的正确映射： ： 。 表示任务层的正确映射， 。 数据 是从未知分布 中采样得到的：

这里， 代表 和 的复合函数。

在真实世界里，我们经常会面临数据的模态信息不完整的问题，即有一些模态是缺失的。设 是所有模态 的子集，我们可以关注只使用 种模态的学习问题，其中 。定义

为只含有 种模态的输入空间，其中 ,   代表第 个模态信息没有被使用。我们可以定义从 到 的映射为 :

类似地，定义 为 到 的映射函数族， 定义 表示从 到 只包括 种模态的映射函数族：

给定训练数据 ，学习的目标是找到 和 ，使得经验风险最小化（Empirical Risk Minimization, ERM ）:

正如[1][2],我们使用群体风险（Population Risk）来衡量模型的学习效果：

举个具体的例子：考虑使用多模态后期融合（Late-Fusion）模型做视频分类。在这种设定中，每一种模态 ，譬如RGB帧、音频、光流或者字幕等，被特定的深度神经网络 编码后，得到的特征经过融合后进入分类器 。假设我们使用 表示某种特征融合操作，譬如self-attention。则 可以表示为 , 是对应的分类器 。

证明一：潜表示空间的质量决定了多模态模型的效果

潜表示空间被用于更好的利用各种模态之间的关联关系，所以我们很自然的会猜测它和多模态学习的效果息息相关。对于已经学习到任意潜表示 ，定义 为它的质量（Quality），即与最优潜表示映射 和任务映射 对应的群体风险差距的下界：

这里， 表示固定 的条件下能取得的最小群体风险。因此一定程度讲， 可以度量由于 和 的差距导致的损失。

定理1：设 是从数据分布 独立采样得到的 个样本。同时，拉德马赫复杂度（Rademacher Complexity）[3]被广泛用于衡量模型复杂度。 在 上训练的模型 的拉德马赫复杂度被记为 。 是 的两个独立的多模态子集，在这 和 种模态上训练分别优化经验最小风险得到了 和 。对于所有的 ，至少以 概率下满足：

其中，

分析： 可以发现在 和 种模态上分别训练的模型效果差距的上限其中一部分是由潜空间的质量差距 决定的。我们可以再进行一轮分析，拉德马赫复杂度 的界通常是 ，其中 表示函数的内在复杂度，由于定理一的 和 都是常数，则定理一可以重新写作：

这表明：随着训练数据的增加（ 变大），使用多种模态训练模型的效果主要取决于它的潜表示空间的质量。

证明二：数据量达到一定规模，模态种类越完整，多模态模型的效果越好

定理一已经在潜空间质量和群体风险差别之间建立了联系，下一个目标是估计已经学到的潜空间表示 和最优的准确表示 之间的差距。下面的定理二表明潜空间的质量其实在训练过程中是可以被控制的。

定理2：依然假设 是从数据分布 独立采样得到的 个样本。 是 的两个独立的多模态子集，在这 种模态上训练分别优化经验最小风险得到了 。对于所有的 ，至少以 概率下满足：

其中，

是中心经验损失。

分析： 考虑 ，根据拉德马赫复杂度的相关性质（参考定理1的介绍）， 、 ，并且有 。从而，如果我们希望更多的模态能产生更好的潜空间（更好的效果），即 ，那么需要满足：

这表明了两部分信息：（1）随着数据量 的增大，模型的内在复杂度的影响会被降低。（2）随着数据量 的增大，上式容易被满足，即使用更多的模态的学习效果优于更少模态的效果。

彩蛋：论文也证明了一个特殊的情况：即当潜空间的映射函数 和任务层的映射 都是线性函数时，

始终成立，即不完整的模态会伤害最优的潜表示，从而降低模型的学习效果。

实验

进入到实验环节。论文也精心设计了实验来验证理论的正确性，可谓是理论与实践结合的典范。

多模态真实数据集实验

这一部分采用了从真实世界收集的多模态情绪分析的数据集IEMOCAP(Interactive Emotional Dyadic Motion Capture)，它包括三种模态：文字（Text）、视频（Video）和音频（Audio）。首先使用离线的特征抽取工具对三种模态信息提取好特征：Audio 100维，Text 100维以及Video 500维。这个数据集的分类有六种，分别是快乐、悲伤、中立、愤怒、兴奋和沮丧。使用了13200条数据做训练，3410条做测试。实验模型上，潜空间的映射使用了一层线性层+Relu，任务层使用了一层Softmax。在对比实验中，如果是单模态模型，则直接进行对应特征映射；如果是多模态模型，则首先进行多模态特征拼接，然后再进行映射。

实验一：多模态学习效果更好。这一部分实验非常直接，见下表，使用全部模态取得了最好的效果。

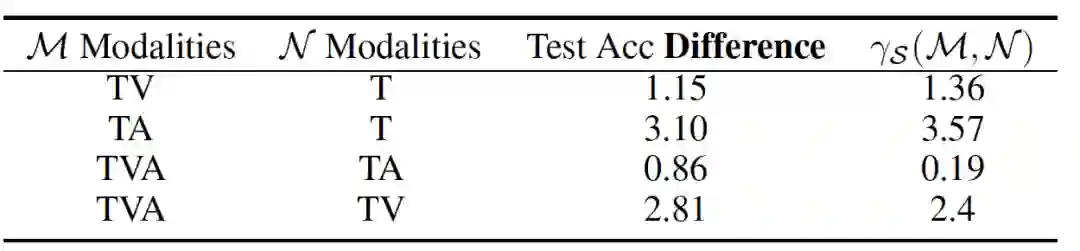
实验二：定理1实验验证。 为了对定理1有一个定量的分析，文章模拟了潜表示质量 的产生过程，即首先未收敛状态下预先训练整个模型，然后再固定encoder 不动，寻找最优的分类器 。已经获得了 和 ， 就可以被量化出来。有一点不同的是， 数学公式里是按照经验损失来计算的，是负数。这里用分类准确率来衡量，是正值。数值越大，代表潜表示的质量越高。如下表所示，使用越多的模态， 值越大。

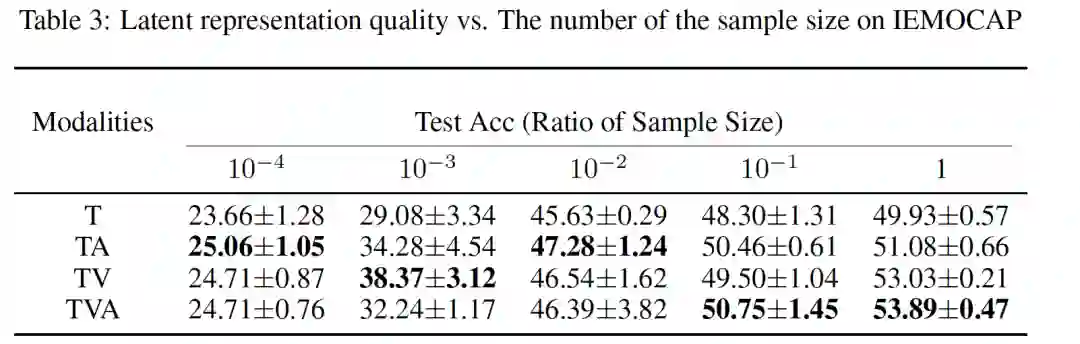
实验三：定理2实验验证。 为了验证定理2，论文在不同量级的训练数据对比了各种模态组合的学习效果差别。如下表，可以看到在训练数据相对较少时，多模态学习并不占优势，可以理解为这时模型的内在复杂度的影响 占主导地位。当数据量到达一定规模，多模态种类丰富性的作用凸显出来。越完整丰富的模态组合，取得越好的效果。

模拟构造的数据集实验

我们知道在真实数据中，模态之间的相关性随任务和数据变化而变化。譬如在知识科普类视频中，视觉信息和字幕文字信息关联程度是很高的，这也是多视角学习（MultiView Learing）经常研究的范畴。而在电视剧剪辑类视频中，视觉信息和文字信息关联程度则很微弱。那么，本文的结论是否在不同程度的模态关联数据上都适用呢？

由于真实数据集很难定量的控制模态相关性程度。为了研究这个问题，论文使用机器自动生成的方式，构造了不同的模态关联数据用于验证。这里考虑三种情况：（1）模态之间完全不共享信息，即每个模态只包含模态特定的信息。（2）所有模态之间共享所有信息，没有区分。（3）介于两者之间，既共享一部分信息，也保有模态特定信息。

数据构造过程：首先使用高斯分布中采样出模态1的特征数据，其中每一个维度都是不相关的。接着我们固定一部分比例的已产生的数据，然后再继续采样生成新的模态数据。这个比例在{0.0, 0.2, 0.5, 0.8, 1.0}之间。1.0表示全部共享，0.0表示全部独立。每种模态含有100维特征，目标是回归拟合1维的label。这个过程共产生了7000条训练数据和3000条测试数据。这里使用了四种模态数据：1，2，3，4。

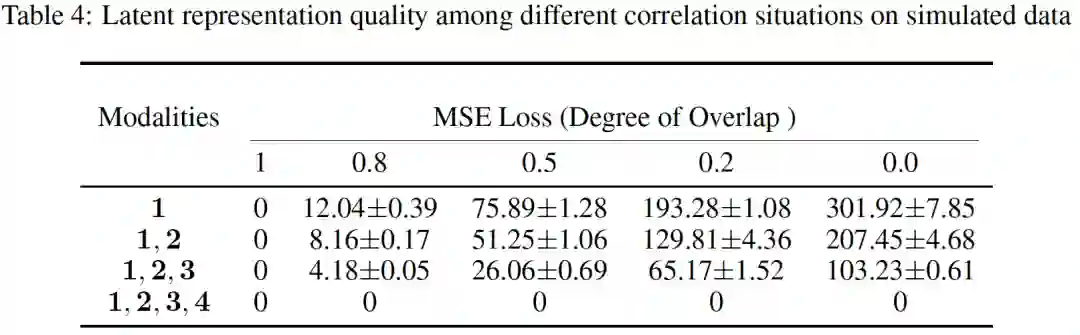
潜表示质量 和模态相关性的关系：如下表所示，首先观察到上文的结论在不同的模态相关性设置中是通用的。另外，模态相关性越高，潜表示质量 也越好，这也非常符合直觉。

结论

面试官：小伙子，你很有前途，明天来报道！

萌屋作者：橙橙子

拿过Kaggle金，水过ACM银，发过顶会Paper，捧得过多个竞赛冠军。梦想是和欣欣子存钱开店，沉迷于美食追剧和炼丹，游走于前端后端与算法，竟还有一颗想做PM的心！

作品推荐

1. 惊呆！不用一张图片，却训出个图像识别SOTA？
2. 视觉增强词向量：我是词向量，我开眼了！

后台回复关键词【入群】

加入卖萌屋NLP/IR/Rec与求职讨论群

后台回复关键词【顶会】

获取ACL、CIKM等各大顶会论文集！

 

[1] Learning from multiple partially observed views-an application to multilingual text categorization https://proceedings.neurips.cc/paper/2009/file/f79921bbae40a577928b76d2fc3edc2a-Paper.pdf

[2] On the theory of transfer learning: The importance of task diversity https://arxiv.org/pdf/2006.11650.pdf

[3] Rademacher and gaussian complexities: Risk bounds and structural results https://www.jmlr.org/papers/volume3/bartlett02a/bartlett02a.pdf