大数据近似计算方法与系统

会员服务 ·

大数据近似计算方法与系统

2019 年 12 月 17 日 THU数据派

转载自：中国计算机学会（ID：ccfvoice）

来源：CCF数据库专委会

本文32500字，建议阅读 82分钟。

本文系统介绍大数据近似计算国内外研究现状、面临的挑战和未来发展方向等。

Tip：本文比较长，约32500字，但本文系统介绍了大数据近似计算国内外研究现状、面临的挑战和未来发展方向等，值得收藏后，利用碎片化时间耐心阅读。

▌摘要 ▌

伴随大数据时代的来临，数据规模爆炸式增长。如何设计出一种能够从大数据中快速准确地搜索重要信息的计算方法成为亟待解决的难题。大数据的特点使得近似计算成为解决这一挑战性难题的关键之一。近似计算不仅具有重要的理论研究意义，而且具有广泛的实际应用价值。在本文中，我们首先从经典近似算法、近似查询处理、系统级近似计算、大数据近似计算四个方面，系统地介绍了近似计算相关领域的国际研究现状和国内研究进展，然后对国内外研究工作的进展进行对比和归纳，最后针对目前近似计算相关研究工作面临的挑战，分析未来该领域的主要研究方向，并对未来发展趋势进行了展望。

关键词：大数据；近似算法；近似查询处理；系统级近似计算；大数据近似计算

▌1 引言 ▌

信息社会的快速发展引发了数据规模的爆炸式增长，使大数据成为继人力、资本之后一种新的非物质生产要素，甚至被认为是关系国家经济发展、社会安全和科技进步的重要战略资源，蕴含巨大价值。今天，大数据已经成为推动行业生产效率提升、促进企业和社会管理变革的利器，并形成规模巨大的产业生态。

由于大数据具有规模巨大、动态变化、可靠性低等特点，传统复杂性理论中关于易解类问题和可近似问题的定义与方法难以适用大数据处理的问题，单纯的算法复杂性或精确性不再是追求的单一目标，快速查询到有效的结果才能满足实际需求。在一些实际的大数据应用中，最优解是难以计算或者不必要的，追求可以高效计算并且满足需求的近似结果具有非常重要的意义。多年来针对这一问题，大数据近似计算从理论到算法再到系统，都取得了许多进展。源于上世纪70年代的近似算法(approximation algorithms)能在多项式时间内处理NP-hard的问题，通常用于处理优化问题；近似查询处理(approximate query processing)则是为SQL聚集查询提供近似查询结果，涉及在线近似查询处理、离线查询处理、查询近似系统三个部分；系统级近似计算(system-level approximation computation)从系统的各个软硬件层，例如编程语言、编译器、存储器和处理器等方面追求实际应用的效果，放松近似算法要求可行解和最优解之间有一个理论界限这一要求，包括软件级近似计算和硬件级近似计算。新型的大数据近似计算主要涉及查询近似和数据近似，具体地，查询近似(query approximation) 将复杂性高的查询转换为复杂性低的查询，不影响查询结果准确性或者影响有限，可用于图模式匹配、轨迹压缩和稠密子图计算等；数据近似(data approximation) 将大数据变为小数据，保留数据主要特征，去除或忽略其中的噪音和错误数据，不影响查询结果准确性或者影响有限，可用于最短路径计算、链接预测等。尽管大数据近似计算并不一定要求理论界限，但它的设计原则不是为了速度牺牲准确性，而是同时注重速度和准确性。

大数据近似计算不仅具有重要的理论研究意义，而且具有广泛的实际应用价值。根据上述大数据的特点和当前近似计算所面临的挑战，我们拟在总结现有技术的基础上，面向大数据，深入探讨传统近似算法、近似查询处理、系统级近似计算、大数据近似计算等四个方面。

▌2 国际研究现状 ▌

2.1 经典近似算法

在计算机科学相关的研究领域中，有许多具有实际意义的问题无法在多项式时间内求得最优解。在这种情况下，寻找算法近似最优的可行解是值得的[1]。近似算法最早定义于70年代[2][3]，研究者广泛认同P ≠ NP猜想，即多项式时间内不能解决NP这一大类优化问题，因此针对这类优化问题的所有可能实例提出了多项式时间的近似算法，找到问题的近似解，并且根据算法最坏情况的相对误差进行评估[4]。近似算法的定义可见于书籍[5]，近似算法是针对NP-hard优化问题提出的一个可以找到近似解的有效（多项式）算法，并且可以保证近似解到最优解之间的界。

在过去几十年的时间里，研究者们对各种优化问题如旅行商问题、装箱问题、最大团问题[1][5-8]等设计了许多近似算法，目前近似算法已是比较成熟的研究领域，使用的技术大体可以归结为以下几种：使用贪心方法的近似算法，目前已用于解决独立集、旅行商问题等；使用序贯算法(Sequential Algorithm)的近似算法，目前已用于解决装箱、图着色问题等；使用局部搜索(Local Search)的近似算法，目前已用于解决最大割、旅行商问题等；使用线性规划的近似算法，目前已用于解决最大割、顶点覆盖问题等；使用动态规划的近似算法，目前已用于解决装箱、背包问题等；使用随机化算法的近似算法，目前已用于解决斯坦纳树(Steiner Tree)、最大割(Maximum Cut)等问题[1][5-8]。

近似算法的相关分析理论也已非常成熟。对于一个近似算法，可按照算法提供的性能保证，也就是近似解与最优解的近似比进行算法的评判，按照近似比，可把近似算法分为常数近似比的近似算法、非常数近似比的近似算法；对于一个优化问题，依次按照是否存在常数近似比的近似算法，是否存在时间复杂度是问题规模的多项式的近似算法，是否存在时间复杂度是问题规模与输入误差参数倒数的多项式的近似算法，分别将优化问题归为APX（常数近似）、PTAS（多项式时间近似）和FPTAS（全多项式时间近似）类[1][5-8]。

2.2 近似查询处理

在线分析处理(OnLine Analytical Processing, OLAP)是数据库系统的核心功能之一。OLAP的性能对于很多在线决策应用来说非常重要。然而，在大型数据集上运行的OLAP查询（尤其是聚集查询）时间较长，无法满足对于实时性的要求。为了缓解这个问题，研究人员提出了近似查询处理方法(Approximate Query Processing，AQP)，为SQL聚集查询提供近似查询结果，通过放宽对结果精确性的要求来换取更高的查询处理速度。AQP针对聚集查询能快速给出接近精确结果的近似结果。我们首先介绍目前主要的两类AQP方法：在线AQP方法基于在线抽样结果回答OLAP查询；离线AQP方法则对数据进行处理生成概要，并使用这些概要回答OLAP查询。之后我们介绍了AQP技术在系统中的应用。

2.2.1 在线AQP

在线AQP通常使用在线聚集(Online Aggregation)的方法进行近似查询处理。在线聚集是一种基于采样理论的近似查询技术，在传统数据库系统中以批处理的模式执行：用户提交查询请求，系统通过迭代的方式使用采样技术对原始数据集进行多轮采样, 最终向用户返回近似查询结果，并返回对应的置信区间。它采用“在线交互式查询”，改进了传统聚集方法中用户被迫长时间等待系统反馈的缺陷，允许用户既可以随时观察聚集查询的进度，也可以动态控制查询的执行和停止[9][10]。根据不同使用环境，本文将在线聚集分三部分进行介绍：单表在线聚集、多表在线聚集和分布式设置下的在线聚集。

2.2.1.1 单表在线聚集

采样和误差估计是在线聚集的必须过程。因此对于最一般情况下的单表在线聚集，研究者主要将研究重点放在如何改进在线聚集过程中的采样方法和误差估计方法上。对于采样方法的研究历史悠久且种类繁多，而误差估计主要有Bootstrap和基于中心极限定理(CLT)两类基础方法。接下来本文将对采样方法和误差估计方法的基本研究情况分别进行介绍。

1.采样方法

采样技术广泛用于近似查询处理[11]。用户在查询前，给定时间限制估算样本集S的大小n，并从原始数据集中抽取数量为n的样本，用以代替原始数据集进行近似结果的聚集处理。

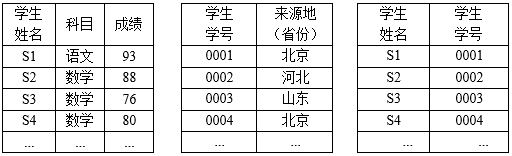
表2.1某班级学生考试成绩表2.2某班级学生的来源地表2.3某班级学生姓名及对应学号

早期的采样技术使用随机均匀采样方法[12][13]，在给定数据分布假设的前提下，多数情况中都可以给用户提供置信区间以对查询结果的准确度进行评估。样本集越大，最终得到的置信区间就越窄，对查询结果的近似就更加精确。但随机均匀采样方法不适用于倾斜数据：如表2.1所示，用户想通过聚集处理方法得到该班级学生语文科目的近似平均成绩，若采用随机均匀采样方法选取样本集，则有很大几率无法选择到作为稀有元组的语文科目的成绩，用户得到的近似结果将是不可信的。

为了处理稀疏数据问题，一些学者提出了分层抽样(stratified sampling)的采样方法，如Agarwal等人[14]建立的BlinkDB系统所使用的采样方法。分层抽样的思路是为稠密元组选取更多数据的同时，为稀有元组选取足量的数据。

总的来说，采样方法各有利弊，研究历史悠久的随机采样方法[13]，仍被广泛使用。这就需要使用者在相应的环境下，选取合适的采样方法对原始数据集进行采样。

2.误差估计方法

在线聚集普遍通过置信区间的形式对结果的可信度进行评估。对于已经被采样方法从原始数据集D取出的样本集S，如果事先已知数据分布类型，误差估计问题可被认为是参数估计的经典统计问题。但多数情况下，数据分布未知，这就要求系统对样本集S的分布进行估计[15]。对样本集S分布类型的估计方法主要有两种：Bootstrap方法和基于中心极限定理的方法。

Bootstrap概念在统计学领域已有较为悠久的历史，并被统计学专业人员广泛使用[16]。Bootstrap方法很早就用于关系数据库中的误差估计[17]，近年来也被广泛用于实现AQP中的误差估计[18]。为估计样本集S的聚集形式θ(S)的分布，可以从整个数据集D中多次随机抽样，但抽样次数可能是几千或万以上数量级的，用这种方法暴力估计θ(S)分布的成本很高，是不可行的[15]。Bootstrap方法旨在通过对样本集S的重采样，用S代替原始数据集D对θ(S)的分布做出估计[19]。Bootstrap从S中抽取样本100次，并通过每一个重采样样本Sk计算θ(Sk)，k=1,2,3,…,100，最终得到θ(Sk)的分布和对应的置信区间[20]，作为对θ(S)分布的估计。Bootstrap方法主要有两个缺陷[20]：一是当聚集函数对稀有元组敏感（如MAX），或样本集S的样本容量太小，不足以支持足够质量的重采样时，Bootstrap对采样分布的估计效果可能很差；二是Bootstrap对采样分布的精确度随着重采样次数增加而增长，在多数情况下，可能需要进行大量重采样，时间成本较高。

在概率论中，中心极限定理指出，对于大量独立同分布、且具有有限数学期望和方差的随机变量（如样本集S），它的某种聚集形式（记为θ(S)）近似服从正态分布N(θ(S),σ2)。而σ可以通过样本集的一个特殊封闭函数(closed-form function)计算得到。例如[20]，当θ(S)是聚集查询中对S进行的AVG操作，此时σ2的估计值s2 = Var(S)/n（Var(S)为样本集S的均方误差，n为样本集S包含的样本数量）。在常用SQL查询中，对于AVG、COUNT、SUM和VARIANCE来说，计算均方误差Var(S)的过程比Bootstrap进行多次重采样的方法更为快捷；但对于MAX、MIN和UDFs (user-defined functions) 等方差难以计算的操作，基于中心极限定理的误差估计方法则不适用。

Bootstrap方法与基于中心极限定理的方法[21]相比，前者通用性更好，但计算成本相对较高；后者有效性很强，但仅适用于简单的聚集查询[22]。

2.2.1.2 多表在线聚集

在线聚集早已被研究可以用于多表情况[23][24]。相较于之前介绍的一般情况下的单表在线聚集，多表在线聚集除了需要考虑采样方法和误差估计方法的选择外，还需对多表联合的情况进行特殊考虑。如对于表2.1学生所在班级，现有表2.2指明了该班级学生的来源地。如果用户想要通过学生的学号查询来源地为北京的学生成绩，则需要联合表2.1、表2.2和表2.3进行查询。对于多表情况下的在线聚集，最关键的问题是多表的连接问题。最直接的方法是遍历全部表进行匹配，将相符的元组一一连接起来。但对于现实中的问题，数据量动辄成千上万，这种暴力求解方法显然无法在实际中使用。因此针对多表连接问题，大量研究提出了不同的解决方案[25-32]。其中由Feifei Li等人[28-30]提出的“Wander Join”是近年来比较典型的方法，接下来将详细介绍该方法作为多表连接方法的案例。

Wander Join[28-31]的基本思想是对于多个需要进行连接查询的表，首先从其中一个表随机选择一个元组作为起始点，然后再依次从其它表以随机选择的方式找到能够与这个元组相连接的元组，起始元组被看作一个顶点，而之后与其他表中元组进行连接的“漫步”操作被看作是构建“边”的过程。以表2.1、表2.2和表2.3构成的多表连接为例，用户想要获得各省份学生的平均考试成绩，Wander Join首先从表2.2中均匀随机地选取一个省份，获取该元组中的学生学号（可能有多个），建立连接，然后在表2.3中进行随机采样，直到找到与所选学号对应的学生姓名，再次建立连接，最后与表2.1建立连接，得到相应省份学生的所有成绩，计算平均值。在随机采样的每个步骤中，Wander Join都通过B-tree索引从下一个表中随机均匀取出可以连接到前一个表所选顶点的元组。为了解决数据的倾斜问题，Wander Join选取了无偏估计方法Horvitz-Thompson estimator[33]。该方法的思想是对于一个路径γ（几个表之间连接的“边”构成一个路径），其采样概率为p(γ)，其聚集结果为v(γ)，则v(γ)/ p(γ)是SUM聚集的无偏估计，最后利用从采样路径计算的多个独立无偏估计量，通过取平均值的方法得到方差较小的无偏估计量。Wander Join方法实用性强，可以嵌入大多现有的数据库引擎中[30]。Feifei Li等人[30][31]在XDB(approXimate DB)中嵌入了PostgreSQL，扩展了PostgreSQL的解析器，查询优化器和查询执行器，以支持CONFIDENCE，ONLINE，WITHINTIME和REPORTINTERVAL等关键字。

对于多表情况下的在线聚集问题，有研究者在如何预知连接体量的问题上做出贡献[32]。然而，对于无法预先知道连接体量的多表连接问题，如何降低计算成本仍然有待研究者进行更深一步研究[15]。

2.2.1.3 分布式在线聚集

当今许多应用程序后台存储的数据量非常大，在这种情况下，人们一般选择使用分布式集群对数据进行存储。而对于具有连接条件和嵌套子查询的复杂查询，需要多次扫描原始数据集。特别是对于分布式存储数据集间的连接问题，在分布式服务器中，需要多次扫描表以将所有表加入查询集，还可能需要跨不同节点进行表的连接，从而导致通信成本高。因此在线聚集在分布式设置下存在两个挑战：一是如何避免多次扫描数据以降低I / O成本，二是如何降低分布式节点之间连接的通信成本[15]。研究者们为克服挑战做出了大量尝试[34-39]，从早期对采样方法的改进[34]到之后结合采样方法和误差估计的改进[35][36]，以及对处理倾斜数据做出的贡献[37]。Srikanth Kandula等提出了名为Quickr的系统人[38][39]，通过无需样本、即时注入采样器的方法来近似大数据集群中复杂的特殊查询结果。作为近年来分布式设置下在线聚集查询的典型案例，接下来将对该系统使用的方法进行介绍。

Quickr使用了Universe采样器，它通过结合Uniform Sampler，Distinct Sampler和Universe Sampler三种采样器，设计策略使不同的数据子集被相对应的采样器处理，实现对多连接输入进行采样的功能；通过在本地将采样器合并到基于成本的查询优化器中，可以在合适环境下自动生成带有相应采样器的采样方案；还使用了一种新的准确度分析方法，该方法可以确保使用采样器的查询方案不会遗漏数据组，并且聚集的近似结果非常接近真实值。

2.2.2 离线AQP

离线AQP技术通过统计原始数据和分析查询负载来生成概要，并利用概要来回答OLAP查询。概要中包含了原始数据的主要特征，但概要比原始数据小得多[10]。常见的生成概要的技术主要包括预抽样(Pre-computed sampling based AQP，简称PSAQ)、直方图(Histogram)、小波变换(Wavelets)、Sketches[10]。PSAQ是具有悠久历史的概要生成方法，采用直接在线下对数据进行抽样作为概要；Histogram是将数据分组聚合结果作为概要的方法；Wavelets是通过对数值序列进行变换提取概要信息的方法；Sketches是针对流式数据进行线性变换生成概要的方法。下面将分别对这四种概要生成方法进行详细介绍。

2.2.2.1 PSAQ方法

PSAQ在线下对数据进行抽样，并用抽样所得的数据作为概要来回答OLAP查询[10]，这种经典做法已有超过30年历史。最简单的抽样方法是针对每个查询，从其中涉及到的表中抽取一定数量的行作为概要。为了减少空间占用，可进一步使用Query Column Set (QCS)-based PSAQ[13]，也就是将不同的查询按照其中用于分组或过滤元组的列集(QCS)进行分组，QCS相同的查询可以使用同一份概要来近似查询。为了处理可能的数据倾斜问题，通常使用分层抽样方法进行抽样，保证较不频繁出现的组内有足够的样本。为了提高置信度，PSAQ通常使用closed-form estimation或Bootstrap方法进行重采样，使用的方法和在线近似查询类似但是可以花更多时间重采样来获得误差更小的结果。

2.2.2.2 Histogram方法

Histogram是一种将数据分组并对每个组（称为bucket）的信息进行统计生成概要[10]的方法。最基本的两种分组方式是通过等宽(equi-width)bucket和等深(equi-depth)bucket进行划分。等宽bucket的每个bucket的区间长度相同，等深bucket的每个bucket包含相同个数的数据项。如对于数值列表{120, 170, 230,250, 290, 350, 417, 460, 470, 560, 630, 673, 732, 890, 983, 1000}, 使用区间长度为200的等宽bucket划分，结果为{(100, 300], 5}, {(300, 500],4}, {(500, 700],3}, {(700, 900], 2}和{(900, 1100], 2}。使用深度为4的等深bucket划分，结果为{(100, 250]}, {(250, 460]},{(460,700]}和{(700, 1000]}。在AQP中Histogram常用于范围计数(range count)查询或点计数(point count)查询。

Histogram的主要研究问题是找到合适的方法划分bucket，bucket数量越少，空间占用越小，但是bucket数量越多查询准确度越高。Histogram的改进方法主要是对空间占用和准确度进行各种权衡，如Singleton-BucketHistogram[40]。Poosala等人[41]系统地研究了直方图的各个方面，提出了一种Histogram分类方法，考虑了各个方面的可用选择，以及这些选择对Histogram有效性的影响。作者为几个分类维度引入了新的选择，通过组合选择派生出新的Histogram类型，研究了如何使用抽样技术来降低直方图构造的代价，并进行了实证讨论，确定了对于谓词范围查询来说总体性能最好的直方图类型。Acharya等人[42]提出了一种快速、接近最优的算法，通过Histogram近似任意一维数据的分布，比现有最好算法快一到两个数量级。Shekelyan等人[43]提出了一种针对多维数据的Histogram，通过在数据密集区域使用高分辨率，在数据稀疏区域使用低分辨率，使得生成的概要更加紧凑。该方法比目前的最好方法精度更高且运行时间相近。

2.2.2.3 Wavelets方法

Wavelets是对数值序列进行小波分解(wavelet decomposition)，并对得到的数值列中选取部分wavelet coefficient作为概要的一种数据概要提取方法[44]。例如对于数值列表{5, 5, 0, 26, 1, 3, 14, 2}，使用经典的Haar小波变换。首先将数值项两两取平均得到{5, 13, 2, 8}（5和5均值为5，0和26均值为13以此类推），这个过程中有一定的信息损失，为了能够还原原始数据，用detail coefficients来表示损失的信息。在Haar小波变换中，detail coefficients是均值与该均值对应的两项中后一项之差，这里是{0,-13, -1, 6}（5-5=0，13-26=-13以此类推）。重复该过程，所得结果如表2.4所示。最终得到变换后的数值序列为{7, 2, -4, -3, 0, -13, -1, 6}（首项为总体均值，后面的项依次为分辨率0-3的detail coefficient)其中的项称为小波系数(wavelet coefficient)。可以看出变换后的序列中从粗到精的包含了原始数据序列的全部特征。在AQP中，从变换后的序列中选择指定个数（通常小于数据大小）个非零小波系数作为概要（该问题称为wavelet thresholding）[44]，常见的策略是保留对还原数据特征较重要的数值（其余设置为0），如保留{7, 0, -4, 0, 0, -13, 0, 0}为概要。在AQP中Wavelet可以用于近似range count查询。

表2.4 一个Wavelets变换的例子

虽然小波变换在信号处理和图像处理领域早有应用，但相比于抽样和histogram，小波变换在AQP领域的研究刚刚起步[10]。Mytilinis等人[44]提出了生成Wavelet概要的一种并行计算方法。通过最小化均方误差、最大绝对误差、最大相对误差三个指标来选择保留的小波系数。传统最小化误差的方法IndirectHaar是基于动态规划的，该文章首先提出了一个动态规划算法的并行化框架，并将IndirectHaar方法并行化，实验表明并行后的算法处理大规模数据时能够线性扩展。为了进一步提高计算效率，提出了一种分布式启发算法DGreedyAbs使误差最小化，实验结果表明该方法在所有数据集上比基于动态规划的算法快2-4倍。

2.2.2.4 Sketches方法

Sketches是一类针对流式数据的概要生成方法[10]。其中AQP研究的一个重要的子类是Linear Sketches，这一类概要可以看作是输入数据序列的一个线性变换[10]，即将输入看作一个矩阵乘以另一个矩阵，得到一个固定大小的矩阵作为数据概要（实际算法中通常用一个hash函数而不是矩阵乘法来完成这种变换）。Sketches理论上可以支持数据库的各种聚集操作，但在AQP的相关研究中，通常每种Sketch都针对一类特定的查询设计。最常见的包括两类[10]：基于频率的Sketch，可以反映数据的总体分布，用于回答“某个值在序列中出现了多少次”的查询[45][46][47][48]；支持count distinct查询的Sketch，用于回答“序列中有多少个不同的值”的查询[47][48][49]。

Flajolet等人[49]最早提出了一种基于概率的COUNT算法来统计数据集合中不同元素的个数，仅使用极小的存储空间扫描一遍数据。该方法可处理大规模数据集，且容易通过分布式进行扩展。针对分布式流数据，Chen等人[47]提出了bias-aware线性Sketches算法（扩展了Count-Sketches和Count-Median）。而Pitel等人[46]提出了Count-Min-Log Sketch，使用基于对数的approximate counters改进了Count-Min Sketch对于低频元素出现频率估计误差大的问题。Pandey等人[48]提出了Counting quotient filter(CQF)支持近似membership查询中的通用算子。Sketches在NLP[50]和实时金融系统中也有应用。

2.2.3 AQP系统

在大数据时代，数据量迅速增加，“由于需要大量的计算和磁盘I/O操作，为复杂查询提供精确的结果可能需要几分钟甚至几个小时”[51]。传统的查询处理在面对复杂查询时无法满足性能需求，而AQP的目标就是通过降低对于结果准确性的要求来提升处理查询时的性能，并且国内外相关学者在AQP方向开展了很多研究，并且取得了一定的学术成果。因此越来越多的人开始关注如何将现有研究成果与应用相结合，针对实际场景解决查询处理的性能问题。目前，有些传统数据库在原有基础上提供了近似查询的功能。同时，许多专用数据库也提出了各自的近似查询引擎，在有误差保证的前提下实现对查询的近似处理。下面将分为两部分对当前采用AQP技术和方法的传统数据库以及各种专用数据库近似查询引擎进行相应的介绍。

2.2.3.1 传统数据库

传统查询处理是专注于以最小化响应时间和最大化吞吐量的方式提供对查询的精确结果[51]。随着数据量的爆炸式增长，传统数据库开始通过近似查询处理的技术与方法来实现近似查询的功能，本节将对Oracle、PostgreSQL、DB2中的近似查询处理进行相应的介绍。

1.Oracle数据库

Oracle公司在Oracle Database 121中，引入了近似查询处理技术，新增了一系列函数:

APPROX_COUNT_DISTINCT_AGG

APPROX_MEDIAN

APPROX_COUNT_DISTINC

APPROX_COUNT_DISTINCT_DETAIL

APPROX_PERCENTILE

APPROX_PERCENTILE_AGG

APPROX_PERCENTILE_DETAIL

TO_APPROX_COUNT_DISTINCT

TO_APPROX_PERCENTILE

可以提供近似查询结果，这些函数的结果与精确结果的误差可以忽略不计。Oracle不仅提供了将精确查询转换为近似查询的方式，还支持在物化视图中使用近似查询处理函数，随后可以将其用于查询重写。

随后，在Oracle 18c2中，APPROX_RANK、APPROX_SUM和APPROX_COUNT三个函数提供了近似Top-N查询处理功能，对其近似查询功能进行了扩充。

2.PostgreSQL数据库

在PostgreSQL 12.03中，pgstattuple模块提供各种函数来获取元组级统计信息。而pgstattuple_approx 是 pgstattuple 的更快替代品，它通过避免全表扫描减少在查询过程中的时间消耗，并且返回近似的结果。在pgstattuple_approx 中，approx_tuple_count、approx_tuple_len、approx_tuple_percent、approx_free_space、approx_free_percent分别输出实时元组数、实时元组的总长度（以字节为单位）、实时元组的百分比等信息，这些结果均是近似的。

3.DB2数据库

DB24数据库通过采样的方法处理高数量级时的大型查询性能。具体操作是通过行级伯努利采样或者系统页面级采样方法，从大规模数据中抽取相应数量的样本，用于回答相关查询，而非采用所有的数据，最终实现对于查询性能的提升。在使用时，可以通过TABLESAMPLE BERNOULLI和TABLESAMPLE SYSTEM分别指定要执行行级伯努利采样或者执行系统页面级采样。

2.2.3.2 专用数据库

近年来，许多研究者提出了不同的近似查询引擎，这些引擎提升了处理查询时的性能。贝尔实验室在1999年提出了aqua[51]，这是一个为数据仓库定制的查询近似处理系统。它通过预先计算概要，减少对基础数据访问次数，并根据Hoeffding和Chebychev界限提供查询结果的概率误差/置信界限，缩短响应时间。微软设计的Quickr[39][38]用于在大数据集群上执行ad-hoc查询，这些集群的性能比BlinkDB、Approxhadoop[36]和Sapprox[37]好得多，它不需对遍布集群的整个数据集进行预先计算，也不必多次查看整个数据。SnappyData[52][53]和FluoDB[54]是两个构建在Spark上的近似查询处理系统。其中，SnappyData结合了大数据计算引擎(Apache Spark)和扩展事务存储(Apache GemFire)，利用近似查询处理技术和各种数据概要，在面对大量数据或者高速流时，使用内存解决方案提供真正的交互式分析。而FluoDB对在线聚集查询进行了泛化，支持具有任意嵌套聚集的一般OLAP查询。犹他大学和香港科技大学的研究人员合作提出的XDB[30]是一个支持在线聚集复杂查询的系统，它可以支持基于最新版PostgreSQL与Wander Join整合的连接运算符，优于早期的DBO[25][27]引擎。IDEA[55]是一个交互式数据探索加速器，它重用了观察到的结果，并且基于概率论重新制订了AQP模型，提出了一种新型索引，这种索引使得用户在没有前期已知工作负载的数据集的稀有子组(rare subgroup of a dataset)中也能找到误差较小的结果。还有许多其他系统也需要离线生成概要和在线估计，例如BEAS(Boundedly Evaluable Sql)[56]和ABS(Analytical Bootstrap)[57][18]。

本节的其余部分将具体介绍BlinkDB、Simba、Verdict等近似查询引擎和数据库。

1.BlinkDB

BlinkDB5由加州大学伯克利分校和麻省理工大学的研究人员设计，是一个大规模并行的、基于采样的近似查询引擎，它建立在Hadoop之上，设计有效策略以选择分布式集群中的适当样本来回答新出现的查询。BlinkDB扩展了Hive / HDFS堆栈，可以处理这些系统支持的同一组SPJA（选择，投影，连接和聚集）查询[13]。它允许用户在响应时间内权衡查询准确性，通过对数据样本进行查询并展示包含了对有意义错误的注释的查询结果，从而实现对海量数据的交互式查询。

BlinkDB使用了两个关键思想：（1）自适应优化框架，可以随时间从原始数据构建和维护一组多维样本；（2）动态样本选择策略，根据查询的准确性、对时间的要求选择适当大小的样本集。基于100节点Amazon EC2 cluster进行了现场演示，在不到2秒的时间内回答了对17 TB数据的一系列查询，查询过程比Hive快200倍，误差为2-10％[13]。

但BlinkDB假设QCS(query column set)是随时间稳定的，这就会生成过多的离线样本，而这些冗余样本对于QCS未被查询工作负载覆盖的查询而言是无效的。为了改进这一缺陷，Sapprox[37]和Approxhadoop[36]在运行时添加了在线采样功能，在运行时可以选择结果表明，Sapprox和Approxhadoop比BlinkDB更灵活。

2.Simba

Simba6是犹他大学以及上海交通大学的研究人员合作提出的一个基于Apache Spark的分布式内存空间分析引擎。它通过系统堆栈扩展Spark SQL引擎，使用SQL和DataFrame查询接口来支持多类型的空间查询和分析。此外，Simba引入了对RDD(resilient distributed dataset)的原生索引支持，以便开发有效的空间运算符，实现低延迟查询。它还向Spark SQL的逻辑和物理优化器引入了空间和索引感知优化以提高分析吞吐量，并通过CBO(cost-based optimizations)模块选择更好的查询计划以充分利用现有索引和统计信息。在大数据集上的实验表明，Simba的性能要优于其他空间分析系统[58]。

3.Verdict

Verdict7是由密歇根大学安娜堡分校研究人员提出的。与其他近似数据库类似，Verdict使用经过挑选的数据样本而非整个数据集，在保证准确性的前提下给出快速、近似的结果。但不同的是，Verdict引入了随机查询规划，保证与数据的交互和即时接口。随机查询规划的主要思想有以下两点：（1）追求不同的近似。除了在小样本上执行原始查询外，Verdict还使用数据中的列、元和时间相关性并发地获得其他几个近似，同时还可以调用现有的回归模型来对给定了其他列组合的特定列的边缘分布或者条件分布进行估计，将其与其他近似结合在一起产生更准确的结果；（2）从过去的查询中学习。

Verdict可以重用之前查询执行的计算，利用当前查询与以前查询之间的相关性和重叠部分，不断改进其近似结果[59]。

最近，相关团队提出了VerdictDB[60]。它的基本思路是通过特殊的方式预先组织数据，以便更快速地进行查询。它使用中间件架构，不需要对后端数据库进行更改，因此可以与所有现成的引擎一起使用。VerdictDB在驱动程序级别操作，拦截发布到数据库的分析查询，并将它们重写为另一个查询，如果操作由标准关系引擎执行，将产生足够的信息来计算近似结果。VerdictDB使用返回的结果集来计算近似答案和错误估计，然后将其传递给用户或应用程序。VerdictDB为各种现有引擎（如Impala，Spark SQL和Amazon Redshift）提供最高171倍的加速（平均18.45倍），同时产生不到2.6％的相对误差[60]。

2.3 系统级近似计算

系统级近似计算(approximation computation)从系统的各个软硬件层，例如编程语言、编译器、存储器和处理器等方面追求实际应用的效果，放松近似算法要求可行解和最优解之间有一个理论界限这一要求[68][74]。系统级近似计算可分为软件级近似计算[61-76]和硬件级近似计算[81-112][139][160]。具体地，软件级近似计算包括软件级近似的策略[61-67]、支持近似计算的编程语言[69-72]，支持近似计算的编译器[77-80]和支持软件级近似计算的分析工具[77][78][80]，而硬件级近似计算包括硬件级近似的策略[68][81][86-91]，支持近似计算的存储器[81][82][84-86][95][96]，支持近似计算的处理器[88][89][91][93][94][103-110]和支持硬件级近似计算的分析工具[111][112]。

2.3.1 软件级近似计算

软件级近似策略主要是在程序层面上为了提高程序的效率与性能而使用的一系列近似计算技术。软件级近似计算的常用策略通常不需要重新设计支持近似计算的硬件设备，仍然使用常用的精确设备配合近似计算软件策略即可完成近似计算。本节将从软件级近似策略、支持近似计算的编程语言、编译器以及一些软件级的分析工具四个角度展开，分别介绍近似计算的软件级原理和代表研究。

2.3.1.1 软件级近似策略

主要的软件级近似策略主要有以下几种：循环穿孔(Loop Perforation)[61-63]、任务跳过(Task Skipping)[36][64]以及减少分支差异(Branch Divergence)[65-67]。

1.循环穿孔

循环穿孔是一种通过转变循环只执行其中一部分迭代来减少计算开销、时间、资源使用[61]的方法。Sidiroglou-Douskos团队最早提出了该方法，并发现该方法能够很好地在多种应用场景运作，相比原始程序，使用该方法后的程序性能提升了7倍，而结果误差限制在10%以内[61]。

2.任务跳过

任务跳过即有选择地跳过一些包含任务代码的代码块，在有界的误差范围内提高程序的运行效率[64]。运用这种策略，Goiri团队提出一种近似机制配合MapReduce程序，其在多个领域应用程序的评估结果表明，该策略能够以较小误差的代价显著减少执行时间与能量消耗[36]。

3.减少分支差异

减少分支差异是一种在SIMD架构中当多个线程执行相同的指令时，通过避免或限制在分支指令上的差异，来提高程序性能的近似计算策略[68]。基于该策略，Grigorian团队提出了一种基于神经网络的解决方法，该方法通过离线训练神经网络来近似核心程序，并直接将神经网络计算代码替代核心程序代码插入到应用程序中。这样将分支代码替换为了不产生差异的计算代码，以有限的质量损失解决了SIMD架构下的分支差异问题[65]。

2.3.1.2 支持近似计算的编程语言

在程序中一旦确认了需要使用近似的数据或操作，就需要通过给源代码加注解[69][70]或使用新的语法[71-73]等方式告知编译器或解释程序执行近似计算，这就需要有编程语言支持各种近似策略。目前有许多支持近似计算的编程语言或框架，主要分为两类：一类是新的编程语言，如Rely[71]、Axilog[73]；另一类是基于已有编程语言的扩展框架，如基于JAVA的EnerJ[69]、FlexJava[70]和基于Rely的Chisel[72]等。

Sampson团队提出的EnerJ是较早能够支持近似计算的编程语言，它主要使用类型限定符来显式声明可能需要近似计算的数据，这样系统会自动把近似的变量映射到更低能耗的存储器上，并使用更低能耗的运算达到节能的目的[69]。

EnerJ需要编程人员确保近似数据不会影响程序的临界数据和存储安全[71]，这样就缺少质量保证，即不能核实程序是否能在多数情况下通过近似计算得到较好的近似结果。与此相反，Carbin团队展示了一种名为Rely的编程语言，它能够让编程人员定量地指定和验证程序的近似计算在多数情况下产生正确的结果，其实验表明当Rely程序在不可靠的硬件上仍能满足这些要求[71]。

但是Rely语言也存在不足，开发者需要自己调整和权衡可靠与节能程度，每次面对各种新的硬件环境时，开发者不得不重新调整代码[72]。为解决该问题，Carbin团队提出一个新的框架Chisel，它能够自动调整，在最大化节能的同时满足对可靠性和精度的规定，这样减少了开发者对两者进行权衡所花费的精力，提高了程序的可移植性[72]。

为了显著减少使用前几种语言时因写注解而花费过的多精力，Park团队为近似编程提出了一套名为FlexJava的语言扩展，该扩展主要具有四个特点：FlexJava是安全的，FlexJava拥有保证控制流安全、内存安全、限制近似的机制，使近似不会导致灾难性的失败；FlexJava是模块化的，FlexJava支持作用域近似、分离式编译，不会妨碍模块化编程和重用；FlexJava拥有一般性，FlexJava能够利用各种近似技术，如循环穿孔、配合基于神经网络加速器等。FlexJava是可扩展的，这让编程人员只需较少的精力去注释一个大型程序。在节省相同能量的条件下，相比EnerJ，FlexJava使用更少的注解，编程人员在写注解上的时间消耗更少，从而减轻了编程人员注解数据或操作的负担，这使得FlexJava成为更贴合编程人员需要的近似编程语言扩展[70]。

2.3.1.3 支持近似计算的编译器

支持近似的编译器使用算法分析和近似策略转换程序的语义，用降低精度的方式换取程序性能提升和硬件能耗下降[74]。目前能够支持软件级近似计算的编译器有ACCEPT[75]、FlexJava编译器[70]等。除此之外，还有一些研究者虽然没有提出新的编译器，但是提出了新的编译优化技术[62][76]。

Sampson团队提出的ACCEPT是一个支持近似的C编译器，主要有两个特点：ACCEPT是受控制的，它保留了程序员用代码注释方式表达近似的意图，并能通过静态分析排除意外的副作用；ACCEPT是实用的，因为它支持了一系列目前在硬件上采用的近似策略，也像传统的编译器一样提供了支持优化的工具，ACCEPT的构建模块能够根据编程人员的引导和动态反馈实施自动近似转换。在基于Intel的服务器、移动SoC和一个超低能耗的微处理器三种平台上，ACCEPT以低于10%的质量损失获得不同程度的速度提升[75]。

Park团队的FlexJava编译器是针对前文介绍的FlexJava语言扩展而专门编写的编译器，与ACCEPT最大的不同点是，它能自动推理影响输出的操作和数据，并有选择地标记它们是可近似的[70]。

除上述介绍的编译器外，一些研究者提出的编译优化技术也同样重要。编译器处理浮点数指令时，由于其语义复杂，通常将该段程序保持与编写时相同，在高性能计算方面优化浮点数计算是重要问题。Schkufza团队针对该问题，采用精度缩放策略，提出了一个基于随机搜索的方法，相比原始代码提升近6倍的时间[76]。Li团队改进了传统的循环穿孔策略，提出一系列编译优化方法，包括基于加载、基于存储的选择性穿孔以及自主动态穿孔方法。在相同误差允许范围内，选择性动态循环穿孔方法的平均速度相比传统循环穿孔方法有较大提升[62]。

2.3.1.4 支持软件级近似计算的分析工具

除了编程语言、编译器对近似计算的支持之外，近年来，一些分析工具例如，灵敏度分析工具[77]、权衡精度与能耗的分析工具[78]和近似应用程序管理工具等[80]，也被开发用来支持软件级近似计算。

灵敏度分析工具用来度量近似程序的变量和操作符对近似计算程序速度、准确性、近似效果的影响[77]。Michel等人[77]提出了一种基于噪声的灵敏度分析工具NAP，具体地，首先通过对程序中的变量和操作符引入独立的高斯噪声扰动，生成程序的随机语义，然后将其转化为在随机程序预期误差的约束下，求解最大化噪声分布的方差问题。最后每个变量和操作符的结果方差表示其灵敏度，方差越大表示其值对扰动越不敏感。这种基于噪声的灵敏度分析方法比基于点估计等方法能更准确地表征灵敏度。

另一部分研究聚焦提供权衡精度与能耗的分析工具，NEAT就属于该类分析工具[78]。浮点单元(FPU)的近似是通过减少计算浮点数位数来节省能耗，NEAT是为应用程序中找到最有效的浮点数实现。它可以帮助用户自动探索各种浮点数实现所导致的精度-能耗权衡空间，一方面可探索通过使用多个浮点数实现精度约束的最低能耗的近似效果，另一方面也可以利用最低能耗的近似效果实现最大精度的浮点数近似[78]。类似地，文献[79]中提出了一种新的近似计算框架ApproxIt，在保证质量的前提下，ApproxIt能够显着提高应用能效。

在近似应用程序管理方面，RAPID管理工具通过利用近似程序的结构信息，加速近似应用的配置、移植和部署等[80]。

2.3.2 硬件级近似计算

硬件级近似计算是从计算机的硬件层面（例如电路、存储器等）支持近似计算。在硬件级完成的近似计算通常包括使用重新设计的硬件设备或在与预定使用条件不同的情况下使用设备，将近似计算在硬件级重新部署，通常需要与应用程序使用接口进行对接来控制错误传播和精确度。本节将依次介绍硬件级近似策略、支持近似计算的存储器、处理器以及支持硬件近似计算的分析工具。

2.3.2.1 硬件级近似策略

支持近似计算硬件的有效设计需要针对不同存储器和处理器，其中存储器包括静态随机存取存储器SRAM[81]，增强动态随机存取存储器eDRAM[82]，动态随机存取存储器DRAM[83][84]，非易失性存储器NVM[85][86]，而处理器包括图形处理器GPU，现场可编程门阵列FPGA 等[68]。本节首先介绍可以在硬件设计上应用的7种近似计算策略[68][81][86-91]。

1.使用精度缩放using precision scaling

精度缩放，是一种通过降低输入或中间操作数的精度（位宽）降低存储或计算要求[87]的方法。利用该方法，Tian等人提出了一种名为ApproxMA的技术，在保证运行时数据精度和差错恢复能力的情况下，ApproxMA能加载精度缩放后的数据用于计算，并在基于混合模型聚类算法的实验上具有节省能耗的能力[92]。

2.使用负载值近似using load value approximation

处理器进行计算前需要从缓存中加载数据，当缓存命中失败时，必须从下一级缓存或主内存中获取数据，这会导致较大的延迟。负载值近似(LVA)利用应用程序的可近似性来估计负载值，因此允许处理器在不停顿的情况下进行处理。这将减少由于缓存未命中而产生的延迟[88][93]。

3.使用记忆存储using memorization

记忆存储方法的工作原理是存储以前函数运行的结果，以便以后使用相同的函数/输入进行重用。通过重用类似函数/输入的结果，能够以一定程度上的近似为代价增大记忆范围，从而提高计算复用的可能性，减少计算代价[89]。

4.使用跳过任务或内存访问skipping tasks and memory accesses

根据帕列托法则（80%的结果取决于20%的原因），对于许多大规模分析任务，人们可能仅需维持少量（比如20%）数据便足以获得高质量的解。由于计算的每个输入、任务对于计算结果的影响一般是不同的。通过有选择地跳过内存访问、任务或一部分输入，算法能够以损失一定计算质量为代价提高计算效率[86]。

5.使用不确定或有故障率的硬件using inexact or faulty hardware

一些近似计算方法会在电路层面设计一些不精确的电路，通过概率计算而不是精确计算得出近似解，另一些方法在不重新设计原硬件结构的前提下，对输入电压进行调节（降低），以可能的误差为代价降低电路的能量消耗，例如在静态随机存取存储器SRAM上降低供电电压可以减少漏能量(leakage energy)，但也增加了读翻转（在读操作期间翻转一个位）和写失败（写错位）的概率[68]。在硬件级近似计算的研究中，该种方法占据非常重要的位置[81-85][94-98]。

6.使用基于神经网络的加速器 Use of Neural Network-Based Accelerators

神经网络(NNs)具有明显的并行性，可以通过专用硬件(NPU)有效地加速，以获得性能/能源效益。由于这种特点，一类近似计算方法利用神经网络来完成近似计算，同时获得有效的并行加速、性能和能源效益[90][99][100]。

7.使用近似神经网络 Approximating Neural Networks

基于在错误容忍应用上对神经网络的观察，研究人员发现神经网络中的计算一大部分对结果影响有限，因此提出了一类近似计算方法针对神经网络进行近似[91][101][102]。

2.3.2.2 支持近似计算的存储器

存储器通常可以通过两大类方法支持近似计算。第一类通过使用有故障率设备对任务中的非关键数据进行处理，而关键数据仍然使用正常设备处理，通过这样的区别对待可以达到在不大量损失计算质量的前提下降低计算消耗的目的[81][82][84]；第二类方法是在特殊条件下使用正常存储设备，降低正常存储设备的一部分可靠性换取能耗的大幅降低[85][86][95][96]，该类方法经常被使用在非易失性存储NVM设备上。

本节按存储器类型，依次介绍SRAM、eDRAM、DRAM、SSD、相变存储器等是具体如何支持近似计算的。

存储器的能耗是系统总能耗的主要贡献者，其能耗很容易受到许多条件的影响。为了保证数据的完整性，设备制造商在存储器上通过深思熟虑的过度设计和“保护带”来避免数据错误。然而，并非所有应用程序都需要100%的正确性。 Shoushtari等人[81]在静态随机存取存储器SRAM上提出了根据应用程序对可靠存储的要求来针对性调整保护带(guard-banding)宽度的技术，使保护带提供的可靠性指标适应应用程序的需求，同时尽可能减少不必要的能耗。这类SRAM称为PFM，用于能在计算中容忍一定程度错误的系统上。部署PFM的潜在优势包括:（1）减少访问能耗，（2）内存模块寿命增加，（3）减少内存访问延迟。实验表明该设计可以在不大量影响可靠性的前提下降低74%缓存漏能量(leakage energy)。

对于增强动态随机存取存储器eDRAM，Cho等人[82]基于人眼对高阶数据(high-order)的变化更敏感的规律，提出了在数据缓冲(data buffer)中降低低阶数据部分的像素准确度和刷新频率来节约能耗的方案。

而对于动态随机存取存储器DRAM，Ganapathy等人[84]设计一种节能错误缓和方案(bit-shuffling error-mitigation)，当使用不可靠的内存时，最小化误差的数量级，将误码的分布偏移到更低位，限制了质量损失，与错误纠正代码(error correction codes)相比，降低了83%的能耗，77%的内存读取时间，89%的电路面积开销。对于自旋存储器STT-RAM，A. Ranjan等人[85]通过降低读数据的电流，缩短读数据周期同时提高电流，缩短写数据周期、降低写数据电流三种方式，以损失可靠性为代价达到减少能耗的目的。

针对固态存储SSD，Xu等人[96]研究发现数据应用可以容忍比SSD的容错目标高得多的误码率，基于此发现提出了降低闪存SSD纠错代码的消耗的机制，提高了40%的性能并节省了1/3的能耗。 Sampson等人[95]介绍了两种近似计算技术，第一种通过减少用于编写多级单元的编程脉冲数，从而允许在多级单元中出现错误。第二种通过将近似数据映射到已经耗尽硬件纠错资源的块上，从而减轻磨损故障并延长内存持久性。

为了改进相变存储器(phase change memory)，Fang等人[86]使用了跳过任务或内存访问的近似计算策略，当需要写入的数据与原数据相同时，取消写操作，在降低有限的性能的基础上节约了大量电能、减少了寿命损耗，并在实验中成功减少了22%的写操作。

2.3.2.3 支持近似计算的处理器

处理器有多种方法支持近似计算，包括降低程序运行时间[91][103]、访存次数[88][89][93]和能耗[94]等。本节将从CPU[88][89][103]，GPU[93][94][104]，FPGA[91]，新处理器架构[105-110]四个方面介绍处理器是如何支持近似计算。

在通用处理器CPU上，Keramidas等人[89]针对使用记忆存储的近似计算方法提出clumsy value cache(VC)的硬件记忆化机制，首先通过硬件缓存一个或一组指令的输出结果，然后通过降低对输入参数的精度要求进行局部匹配，提高旧指令结果直接成功重复使用的可能性。而Venkataramani等人[103]提出了质量可编程处理器，可以通过指定指令级别的质量来降低不必要的电能损耗。 Yazdanbakhsh等人[88]提出了Rollback-Free Value Prediction(RFVP)，使用近似值预测机制，当某些近似安全的加载操作在缓存中不命中时，RFVP预测出需要的值，避免一部分由于缓存不命中而进行的加载操作，大幅提升了性能并降低了能耗，该项技术在GPU上也可以应用。

在图形处理器GPU上，Sutherland等人[93]提出了一种类似RFVP[88]的纹理缓存近似方法，使用GPU纹理拾取单元（GPU’s texture fetch units）产生近似值，从而消除总体存储器访问的代价，他们在NVIDIA 780GTX上进行的实验表明，该方法减少了12%的运行时间，却只增加了0.4%的输出错误。 GPU的高并行特性会产生很高的能耗，因此Rahimi等人[94]以减少GPU计算能耗为目的，提出approximate associative memristive memory (A2M2)微架构设计，对于低电压下的GPU应用，在其计时误差可容忍的前提下，内核平均节能32%。基于同样的目的，Zhang等人[104]提出了将近似计算应用在GPU的浮点数和某些常用函数计算中来减少能耗的技术，实验表明该技术可以在对计算质量没有显著影响的前提下降低32%的能耗。

在现场可编程逻辑阵列FPGA上，Roldao-Lopes等人[91]研究发现，对于循环，降低计算精度并提高循环次数可以达到同样的总体精度，然而通过这样的近似操作可以大幅提高程序的并行运行能力。该研究通过平衡迭代次数和操作精度来优化性能，从而比双精度实现的速度提高了几倍，在达到相同精度的最终结果的情况下，将程序平均加速26倍。

另一些研究则是改变处理器的架构，以更好的支持硬件级近似计算[105-110]。主要包括，从支持容错的处理器架构[106][107]、指令级扩展的角度改变处理器微架构[105]，和针对神经网络优化的处理器架构[108-110]。

随着半导体技术向更小的晶体管尺寸扩展，硬件故障率正在增加，一些研究聚焦如何在处理器架构上应用容错技术。 Yetim等人[106]提出并评估了在一个由不可靠结构构建的通用处理器上运行容错软件的技术，同时从微体系结构的角度研究了在应用程序输出中仍然产生有用结果所需的最小错误保护。与此同时，Yetim[107] 也针对易出错硬件上程序并行执行的挑战，提出了一种低开销的通信保护机制CommGuard。 CommGuard使用基于有限状态机的检查器来填充和丢弃数据，以保持程序控制流与处理器互相通信的数据之间的语义对齐，从而在易出错的硬件上实现并行计算线程间通信的正确性。

Esmaeilzadeh等人[105]提出了一种支持指令集扩展的微架构Truffle，它从硬件角度以牺牲精度为代价节省能耗。作者首先提出一种指令集扩展，使其支持了近似的操作和存储。然后，利用双电压操作（高电压用于精确操作，低电压用于近似操作）设计了一种有效支持指令集扩展的微架构Truffle。在几种基准测试中，Truffle具有43%的节能效果。

针对深度神经网络运算密集型和存储密集型难以硬件部署的问题，近年来的研究提出一些针对神经网络优化的处理器架构。 Esmaeilzadeh等人[108]设计了神经网络处理单元(NPU)，并低开销耦合NPU和处理器流水线。他们首先提出了一种基于学习的方法来加速近似程序，然后，选择并训练神经网络来模拟代码区域，再通过NPU的低功率加速器来替换原始代码，最后，NPU与处理器流水线紧密耦合，以加速代码区域计算。而Han等人[109]实现了压缩的稀疏神经网络的硬件加速，提出的EIE (Efficient Inference Engine)方法应用于硬件，在CPU，GPU上分别得到了189倍和13倍的效率提升。对于特定的神经网络，例如长短期记忆模型，Han等人[110]也设计了新的专用编译器以及专用处理器架构并同样结合深度压缩，大大提高运算能力。

2.3.2.4 支持硬件级近似计算的分析工具

一些分析硬件近似计算的工具，例如近似检查器[111]和量化分析工具[112]等被用来检测硬件级近似的错误。

近似检查器是检测程序执行中支持近似计算的硬件可能出现的错误，以确保程序无错误的运行[111]。一般通过大量的冗余来检测硬件的故障，但会引入非常高的开销。 Mahmoud等人[111]设计了一个浅层低成本的神经网络方法，通过快速识别程序执行过程中发生的错误输出，判断是否会有硬件损坏。在金融分析、机器人、图片处理等应用的基准测试集中，近似检查器都达到了很高的精度。

另一些研究则是量化研究了动态指令中执行的错误对程序的影响。 Venkatagiri等人[112]提出了Approxilyzer量化分析工具，它能够以较高精度(平均95%)对执行的所有动态指令中单比特位错误(single-bit error)的质量影响进行量化。该工具可用于定量地调整输出质量、弹性和开销，从而实现超低成本的弹性解决方案。

系统级近似计算是从计算机整个系统的角度上介绍如何支持近似计算的，可分为软件级近似计算和硬件级近似计算。软件级近似计算涉及在程序层面应用的近似策略以及支持这些近似策略的编程语言、编译器和分析工具；硬件级近似计算涉及硬件层面的近似策略和支持近似计算的存储器、处理器以及分析工具。系统级近似计算的本质是从不同的层面，通过放松对计算结果高精度的追求以换取计算效率提高或能耗降低等实际追求。

2.4 大数据近似计算

大数据近似计算专门针对大数据问题，有针对性的提出有效的处理方法，包括通过尺度无关性界定仅需处理小数据即可获得精确结果的查询，避免直接处理大数据；通过有界查询从大数据识别出所需小数据；对于无法仅处理小数据的查询，采用基于数据驱动的有界近似算法，获得满足一定精确度的近似解。

1.尺度无关性理论

Fan等人提出了尺度无关(scale-independent)查询并研究了其相关性质[113]。对于这类查询，存在一个数据的子集，该子集大小仅与查询本身和访问方式有关，与数据全集大小无关(scale-independent)。而在该子集上运行查询所得结果与在全部数据上运行查询所得结果相同。尺度无关性刻画了大数据下通过访问有限数据进行精确查询处理的可行性，带来的问题是能否判断哪类查询具有尺度无关性，以及当无法快速判断尺度无关性时，能否找到尺度无关性的充分条件，降低判断的复杂度。

2.有界查询理论及算法

对于尺度无关查询，Fan等人提出了基于访问模式的有界可评估(bounded-evaluable)查询的概念，用以识别回答查询所需的小数据[114]。求解此类查询的开销仅与查询本身及约束有关，并证明了部分一阶逻辑查询是有界可评估查询。并研究了识别此类查询所需小数据的方法。基于该方法设计了Conjunction Query查询算法[115]和图匹配算法[116]。

3.数据驱动的有界近似计算

当一个查询不是有界可计算时，基于访问模式无法通过查询有限数据得到精确查询结果。因此能否通过查询有限数据得到满足。Fan等人提出了一个以资源比(resource ratio)和精确度为参数的有界近似查询处理方案[56]，资源比约束了能访问的数据所占数据总量的比率，精确度刻画了用户所能接受的近似解与精确解之间的距离。

▌3 国内研究进展 ▌

3.1 经典近似算法

经典近似算法相关的研究从70年代起就已经在国际上如火如荼地进行，不少难解的优化问题都已经被不同近似比的近似算法解决[1][5-8]，目前很多经典近似算法都是由国外提出的，国内相关研究工作的开展相对落后。但是值得注意的是，近年来不少国内研究者及其团队开始投入近似算法领域的研究，且取得了不少进展，在该领域上不断缩小与国外研究团队的差距：清华大学的姚期智教授近年在博弈拍卖理论相关的最大收入(maximum revenue)问题[117-118]上取得进展；北京航空航天大学的李昂生教授带领团队研究包括最大快乐顶点和边(happy vertices and edges)问题[119]、最小污染问题的复杂度和可近似性分析[120]、不平衡图分割问题[121]等近似算法及分析；中科院计算所的孙晓明教授带领团队研究包括解决最大团问题[122]和独立集与顶点着色问题[123]相关的理论分析及近似算法；上海财经大学的陆品燕教授及团队近年在边覆盖问题[124][125]、立方图(cubic graph)图着色问题[126]的完全多项式时间近似算法上取得突破；中科院软件所的夏盟佶副教授和团队在计数复杂度方面进行研究，代表研究包括全息算法(holographic algorithms)[127][128]等。

除了专门在近似算法领域开展研究工作的研究者，在其他领域如数据库领域的研究者也通过引入近似算法，对数据库领域的相关问题寻找新的解决办法：哈尔滨工业大学的李建中教授带领团队通过使用近似算法，解决了包括冲突图(conflict graph)的顶点覆盖问题[129]和最连通顶点(most connected vertex)问题[130]等；北京航空航天的马帅教授及团队，通过应用近似算法解决了在时态图中查询稠密子图问题[131]，也将近似算法应用在了异常检测中[132]；中国人民大学的魏哲巍副教授及团队通过使用近似算法在结合属性的Top-k查询[133]、范围计数(range counting)[134]等问题上有所进展。

3.2 近似查询处理

在近似查询处理领域中，国内学者的研究主要集中在在线AQP领域[135-137]，而离线AQP和查询近似处理系统国内学者的研究较少[56][138]。

对于在线AQP领域的研究，东南大学的Wang等人[135]对分布式条件下的在线聚集研究做出贡献。针对在线聚集在MapReduce环境下的两点限制：(1)对数据偏斜缺乏考虑导致的低采样效率(2)由MapReduce的独立作业执行机制引起的高冗余I/O成本。Wang等人提出了云系统中的在线聚集提出了改进方案，并提出了一个新的基于MapReduce的云系统OLACloud，以便更好地支持不同数据分布下的在线聚集和大规模并发查询处理。该研究包括一是提出了一种基于公平分配块布局的内容感知重划分方法，以提高采样效率并同时保证存储和计算负载之间的平衡；二是开发了一种共享采样方法，在多个查询之间共享采样机会，从而降低冗余的I/O成本。针对分布式条件下的近似聚集I/O成本高问题，浙江大学的Zhang等人[136]提出了一个I/O高效的分布式近似框架，以支持大型数据集的任意子数据集的近似。该文献中提出了一种基于集群抽样的近似CLAP分布感知方法，对于在线聚集方面，该框架主要针对缺乏对子数据集不均匀存储分布的考虑，致使在不均匀分布的子数据集上I/O效率低和估计准确性差的问题提出改进。哈尔滨工业大学的Han等人[137]提出了可以用于在线聚集的采样新方法，仅使用小部分数据就可以高精度地计算聚集结果。文献[137]中针对采样过程中，抽取到数据集中只占有限比例、但离群程度较高的数据对聚集结果影响较大这一问题，通过引入杠杆从统计角度反映数据的个体差异对全局答案的不同影响。该方法同时使用两种估计器——基于杠杆的估计器和草图（聚集结果的“粗略图”）估计器，生成了两个估计量，对估计量的偏差进行了评估，然后将它们置于约束关系中，并根据实际情况确定偏置条件，对估计过程进行迭代改进，直到二者结果的差值低于阈值。由于迭代机制和杠杆的协同作用，使用该方法进行的近似聚集结果达到了较高精度。此外，该方法无需记录采样数据的特点使其非常适于大数据的在线聚集处理。

目前，国内对离线AQP的研究相对较少。清华大学的李国良教授团队提出了一个有界近似查询处理框架(Bounded Approximate Query Processing，BAQ)，给定误差界限和一组查询，BAQ从数据中选择高质量的样本，离线生成统一的概要，基于生成的概要回答在线查询。BAQ只需要生成一个统一的概要，而不必为每个查询都生成概要，所以概要的规模较小，同时BAQ的误差更小。通过在微软产品数据集上进行实验发现，与当前方法相比，BAQ同时减少了10-100倍的概要数目和误差[138]。

对于查询近似处理系统，目前国内的相关成果大都是与国外人员合作完成的。例如，Simba是一个基于Apache Spark的分布式内存空间分析引擎，上海交通大学的研究人员参与了其设计与实现。此外，BEAS(Boundedly Evaluable Sql)是一个可以评估每个查询计划的可行性并选择更好的查询计划的系统，是由北京航空航天大学与英国爱丁堡大学合作完成的[56]。

3.3 系统级近似计算

在系统级近似计算领域中，国内对于软件级近似计算子领域的研究较为欠缺，关注重点主要集中在硬件级近似计算子领域[86][92][97][139]。

3.3.1 软件级近似计算进展

目前国内对软件级近似计算相关的研究，包括软件级近似策略、支持近似计算的编程语言、编译器、分析工具等相关领域的研究工作几乎处于空白阶段。用于支持近似计算的编程语言、编译器、分析工具都属于底层软件或低级语言，国内缺乏该领域的研究人才和团队，因此，在这方面的研究深度明显不足。

3.3.2 硬件级近似计算进展

在国内，硬件层面的近似计算的研究发展呈现起步晚、不成体系的特点，与国际研究差距较大。国内主要的研究也可以分为近似存储器和近似处理器两大方面。

在近似存储器方面，中国科学院Fang的团队提出了SoftPCM[86]，在Phase Change Memory上，如果需要写入的数据与原数据相同，则取消写操作，在降低有限的性能的基础上节约了大量电能、减少了寿命损耗。除了对存储器本身的改进，近似计算技术还可以应用在访存方式上，香港中文大学的Tian团队通过进行芯片外数据访问的动态精度缩放来减少访存能耗，基于此提出了新的近似内存访问技术ApproxMA[92]。

有团队在近似处理器的电路层面设计新的计算器（如乘法器[139]、乘积之和[97]）等近似门电路，用一定的近似代价换取低能耗。南京航空航天大学的Liu的团队设计了两种新的近似计算乘法器，在有一定错误容忍能力的同时实现节能[139]。类似的，基于牺牲准确率换取低能耗、少时间的思想，上海交通大学的Su等人团队提出一种两级逻辑综合近似的启发式方法，能够在给定错误率约束情况下，辨认一种SOP(sum-of-product，乘积之和)的表达式[97]。上海交通大学的Wu等人[98]还在布尔网络电路表示上，提出一种新的多级逻辑综合近似框架，基本操作是近似简化布尔网络中的节点。在此框架上，又对于三种不同类型的错误率约束提出了三种不同的算法，第一种算法ALFANSER只处理错误率约束。第二种ALFANSER-MEM，它处理错误率和最大错误量约束的组合。第三种ALFAN-ER-AEM，它处理错误率和平均错误率约束的组合。这三种算法都在每次迭代中反复选择一个最有效的节点进行简化。

3.4 大数据近似计算

大数据规模巨大、动态变化、可靠性低。因此，一个新的研究方向是如何设计近似计算方法从大数据中快速准确地提取有价值的信息。

大数据近似计算[4]面向具体场景下的大数据问题，利用查询近似和数据近似的指导思想，挖掘任务和数据中提高计算效率的特征，简化任务和数据的复杂度，设计高效的解决方法。不同于近似算法的研究，大数据近似计算不拘泥于可行解和最优解之间理论界的要求，更加追求实际中的速度和准确性[4]；大数据近似计算也不同于近似查询处理，相对更侧重查询处理算法而不是系统。此外，大数据近似计算的方法不是为了速度牺牲准确性，而是同时注重速度和准确性，尤其是两者之前的权衡。

3.4.1 查询近似

在大数据分析任务中，查询近似将一类计算复杂度高的查询变换为另一类计算复杂度低的新查询，通过执行新查询得到满足要求的近似解。在进行变换时，查询近似需要在查询效率和解质量之间取得平衡。下面分别介绍几个基于查询近似思想的具体研究工作：大数据条件下的图模式匹配，轨迹数据在线压缩以及时态稠密子图的搜索。

图模式匹配[143]是指给定一个模式图Q和一个数据图G，找出G中与Q匹配的所有子图。经典的子图同构方法虽然能完整保留模式图和数据图之间的拓扑结构，但计算复杂度过高（NP完全）无法用于处理大数据，且在某些情况下过于严格而难以找到合理的匹配[144]。一些子图同构的替代方法[144-146]能够在立方时间内进行图模式匹配，但匹配结果可能与模式图存在非常大的结构差异，并且通常太大而难以分析。 Ma等人提出了强模拟的概念[140][141]及强模拟的分布式算法[142]，用以解决大数据条件下的图模式匹配问题。强模拟能够保留模式图的关键拓扑结构并找到一组有数量限制的匹配结果，其计算时间复杂度与[147][144]相同，同时具有局部性特点。作者基于此特点开发了一个高效的在分布式图上进行图模式匹配的分布式算法[115]。实验表明，强模拟能够识别出子图同构未能识别的合理匹配，并找到保持图拓扑结构的高质量匹配（含有70%-80%的子图同构匹配）。此外，强模拟比子图同构快100倍以上。

Lin等人[148]提出了一种单次遍历的在线轨迹压缩方法，将一条轨迹上的数据点压缩为一组连续的路线线段。现有单次遍历算法的时间和空间复杂度低，适合于在线处理，但难以达到有效的压缩率。同时由于采用了全局距离检查导致一个数据点可能会被多次检查。提出了一个局部距离检查方法，确保每个数据点在整个处理过程中仅被检查一次。基于该方法开发了单次遍历且有误差限界的轨迹简化算法。实验表明该算法比FBQS（当前最快的LS在线算法[149]）快四倍以上，并与DP（当前压缩率最好LS批处理算法[150]）的压缩率相当。

Ma等人[151]研究了稠密时态子图的求解方法。对于道路交通路网这一类特殊的时态网络，其节点和边固定不变，但是边的权重持续随时间戳变化。稠密时态子图被定义为一个连通子图，其“稠密程度”通过其所有边在一段时间间隔内的权重之和来度量[152]，如道路网络上一个在一段时间内持续拥堵的道路集合（即堵塞区域）。稠密时态子图可用于城市道路交通分析，对大城市的运输管理有重要意义。当前最好的解决方案MEDEN[152]采用过滤并验证的方法，当时态网络包含大量的节点/边或时间较长时不可扩展。作者提出了一个数据驱动的方法，从所有可能的时间间隔中识别出最有可能（具有概率保证）的k个时间间隔（k是一个小的常数）。其主要思想来自对交通数据中演变趋同现象的观察。在真实及模拟数据上的实验表明，该方法比MEDEN快一千倍以上，并且找到的稠密子图的质量与MEDEN相当。

3.4.2 数据近似

大数据规模很大，因此，大数据分析任务的一类解决思路是将给定的大数据转化成更小的数据，使得查询可更快的返回结果。不同于近似查询处理，数据近似查询可能返回精确的查询结果。需要指出的是，数据近似不适用于某些数据分析任务。例如，一个线上商店需要统计其目录中商品的总数量。在这个任务中，所有的商品基本上都应当纳入考虑，如果仅选择（小）部分商品，那么很难得到满意的结果。下面分别介绍两个基于数据近似思想的具体研究工作：大规模图数据上的最短路径/距离查询，以及大规模网络中的链接预测。

计算最短路径和最短距离是图中的基本问题之一。目前最好的算法[155]的时间复杂度为O(nlogn+m)（n和m为图中节点数和边数）。然而在处理大规模图数据时该方法的效率依然无法令人满意。 Ma等人[153][154]提出了一种轻量级的数据缩减技术来加速大规模带权无向图上的（精确的）最短路径和最短距离查询。作者提出了代理节点的概念，代理节点是最短路径中的一些关键节点，每个代理可代表图中的一组节点（称为DRA），少量代理即可表示图中的大量节点，由相同代理表示的节点集合内的最短路径和最短距离可被高效地求解。作者基于此概念提出了一种两阶段的最短路径和最短距离计算方法，预处理阶段在线性时间内找出所有“代理”节点及其DRA，并计算从任意节点到其代理的最短路径/距离，然后移除所有DRA得到仅包含代理的子图。在查询应答阶段，在仅包含代理的子图上计算代理间的最短路径，与预处理阶段的路径拼接后即得到最终结果。实验表明，真实的社交网络和路网中大约有1/3的节点可以被代理捕获。

链接预测是基于网络中链接的变化历史预测未来链接形成的任务，在推荐系统中有较多应用。由于链接预测方法常用于非常大且稀疏的网络中，其搜索空间高达O(n^2)（n为节点个数），大多数现有的链接预测算法仅通过所有可能产生链接的一个子集来评估产生链接的可能性。 Duan等人[156][157]提出了一种基于集成的链接预测方法。该方法首先通过有性能保证的结构化bagging方法将搜索空间分解成一组小矩阵，然后使用隐语义模型(latent factor models)来处理分解后的小规模（更稠密）网络。实验表明，在真实的社交网络上，该集成方法比BIGCLAM[147]快50倍以上，同时准确率提升20%以上。

▌4 国内外研究进展比较 ▌

从以上分析和总结可以看出，国际学者对经典近似算法、近似查询处理、系统级近似计算和大数据近似计算开展了广泛而深入的研究，奠定了相关领域研究的基础。在此基础上，国内的研究者在相关的领域也开展了许多深入的研究，并取得一些重要的成果。

经典近似算法在70年代由国际学者率先提出，经过50年的发展该领域相对成熟，国内学者相关研究开展较晚，但近年来在该领域持续跟进，国内外差距逐渐缩小。在近似查询处理领域，国内研究主要聚焦在线AQP部分，而离线AQP国内研究相对较少，并且在查询近似处理系统部分，国内还只是参与了部分系统的研究工作，到目前仍没有完整的查询近似处理系统。在系统级近似计算领域，硬件级近似计算逐渐产业化，国内在支持硬件的处理器等部分开展了神经网络芯片等新领域的研究；而对于软件级近似计算，国内几乎没有开展相关的研究。大数据近似计算则是一个新兴的领域，国内学者也对其开展了深入的研究，并取得有影响力的成果。从整体上看，国内的研究同国际相比，具有一定差距。

▌5 发展趋势与展望 ▌

1.经典近似算法

经典近似算法经过几十年的发展，到目前为止该领域已经相对成熟，近似算法的研究逐渐从理论到实践，即不再局限于基础理论，而是结合当前最新领域的具体实际问题和数据[122][123][127]，同时追求近似算法在实际运用中也能保持较高的速度和较低的近似比。

2.近似查询处理

随着大数据时代的到来，数据量的增加和分布式存储的应用对近似查询处理提出了新的要求和挑战。首先，越来越多的系统要求高精度、高速度以及使用有限的资源，所以如何在有限的时间、空间和给定的误差精度内提供需要的近似查询结果是一个很有意义的研究内容[15][138][158]。其次，目前AQP的应用大都是根据特定的场景进行设计，缺乏一个统一的框架，如何对AQP共同特征进行提取，制定一套类SQL查询的AQP语言标准将是未来研究的一个重要方向[15]。同时，为了更好地提高在线聚集的效率，并且保证聚集结果的质量，有学者如今致力于协同结合在线和离线AQP的优势[159]，以期使聚集系统不断适应工作负载和可用存储资源的变化。但如何处理数据倾斜问题和如何在保证近似质量的前提下提高分布式环境中的数据I/O效率，仍是在线聚集领域亟待研究的挑战性问题。

当前许多专用数据库使用近似查询引擎时都需要将其绑定到特定的平台，并且需要彻底更改之前的数据库结构。传统的数据库供应商出于对成本的考虑，不愿对其遗留代码库进行大规模更改，这就造成了在AQP相关学术研究持续推进的背景下，实际的工业应用却较为稀少的现象。因此，在推广AQP应用的过程中推出配套的引擎或中间件，以减少对原有产品的更改，也是当下一个值得关注的研究重点[60]。

3.系统级近似计算

精确计算的软件工程通过抽象和组合，从布尔代数开始并逐步完善，实现了复杂可靠代码的构造。然而目前还没有一种通用的方法来描述不可靠的硬件[160]，也没有用于产生确定性结果的高级语言库例程的API。例如，许多近似计算工作已经显示出输出的图像[92]，并要求读者对其质量进行主观评价，然而主观评价并不能支撑设计、优化和制造一个合适的近似计算系统。制造商在生产硬件时需要一些指标来保证给定零件的近似计算质量。在应用程序编写时也需要API[82]来控制错误的出现和在整个系统中的传播。

现有的大多数近似计算研究都侧重于多媒体应用（图像、视频等）和迭代算法。然而，这些容错工作负载只占计算工作负载的一小部分。未来的近似计算研究势必将范围扩展到整个计算应用领域[68]。然而单种近似策略就可能对其他组件的操作产生无法预见的影响，并可能导致不可接受的错误计算结果。在未来的研究中，需要综合评估近似计算对整个系统的影响，以及近似计算在多个部件中的使用情况。此外，在系统中使用多个近似策略，如精度压缩[87][92]、负载值近似[88][93]和动态电压/频率缩放[68][81-83][85]，确保这些方案能够协同工作对于近似计算在商业系统中的顺利集成非常重要。

虽然近年来近似计算得到了显著的发展，但它仍处于起步阶段[68]。目前近似策略的实施通常集中在硬件[81][91][94]或软件[36]上，在未来应用程序对近似策略的要求必然会使软件和硬件在近似策略上相互配合，这就要求应用程序有效地将精度要求传达给底层平台并在运行时监控计算质量，这给程序员带来了沉重的负担。因此需要将现在的近似计算研究阶段的编程框架转换为未来成熟而健壮的代码开发平台[160]，该平台需要充分利用不可靠硬件和近似计算应用程序的特点，从繁杂的确保应用程序质量的工作中解放程序员，进行更方便的近似应用程序开发。

4.大数据近似计算

大数据近似计算是一个新兴的研究领域，针对传统算法设计面向大数据时产生的性能瓶颈，以理论与实践结合作为指导思想，从算法复杂性最优为导向转为理论可靠和实践有效为导向，充分分析挖掘任务与数据的特征，基于任务和数据的特征研究设计面向大数据场景的高效算法。

具体来说传统算法设计存在三类问题。首先，传统算法设计旨在提出处理给定问题下任何实例的算法，通用性良好，但由于算法的复杂性由问题的最难解实例决定，这导致在处理该问题的易解实例时，仍然采用和处理难解实例的完全相同的复杂处理方法，不能针对性的高效处理这些易解实例，导致了计算资源的浪费。其次，传统算法设计通常缺乏对隐含在任务和数据中的实例特征的深度挖掘，以至难以实现特定应用场景下的有针对性的提高计算准确性与效率。再次，由于大数据具有规模大、变化快、结构多等特点，使得传统算法复杂性理论难以适用于大数据计算场景。如一个时间复杂度为O(n^2)的算法的问题在传统复杂性理论中属于易解类问题，但在大数据场景下该算法的复杂性就有可能是难以接受的，其易解结论难以具有普适性，需要具体问题具体分析。

大数据近似计算未来可能的研究方向包括：如何感知和提取任务和数据中能够提升计算效率的特征？如何结合任务和数据特征与算法设计结合起来设计面向大数据的高效算法？如何通过有限的资源尽可能求解更加精确的结果？

此外，大数据并行近似算法和系统的研发也是未来的发展趋势。

▌6 结束语 ▌

信息社会的快速发展引发了数据规模的爆炸式增长，随着计算设备的微型化和普及化，各类传感器、智能手机、可穿戴设备、计算设备无时无刻不在产生着数据，如何从大数据中快速准确地搜索有价值的信息已成为当前亟待解决的一个重要挑战性问题。大数据近似计算的研究与开发不仅具有重要的理论研究意义，而且具有广泛的实际应用价值。国内的大数据近似计算研究正在快速地发展，但是与国外已经开展了二三十年的科研积累相比，尽管质量尚可，但由于研究团队明显少于国外，研究起步晚，研究系统性差距很大，仍然需要奋力追赶。希望在未来我国可以出现更加丰富的大数据近似计算领域研究成果。

▌作者简介 ▌