干货 | 上海交大CS系博士生李泽凡：利用高阶残差量化（HORQ）方法进行网络加速

AI科技评论按，神经网络的压缩和加速现在已经成为一个热门课题，这个领域有多种研究方法，网络量化就是其中之一。网络量化分为输入量化和权值量化两种。而同时将输入和权值量化会造成网络精度的大幅下降。在Performance Guaranteed Network Acceleration via High-Order Residual Quantization (性能保障的高阶残差量化网络加速方法)一文中，作者针对这个问题，提出了高阶残差量化（HORQ）的方法，既能够利用网络量化带来的大幅计算加速，又能够保证网络的精度不会大幅下降。

在近期雷锋网 AI研习社的线上分享会上，该论文第一作者李泽凡为我们详细解读了HORQ方法及相关推导过程 。

李泽凡，上海交大 CS 系二年级博士生，师从高文院士和张文军教授。 研究方向为神经网络理论、网络加速和压缩。

分享内容：

大家好，今天我将为大家带来我们在ICCV 2017上发表的文章——Performance Guaranteed Network Acceleration via High-Order Residual Quantization (性能保障的高阶残差量化网络加速方法)。

这篇文章的研究领域是网络加速和网络压缩。主要的网络加速和网络压缩方法可以分为如下三种类型，第一种是网络剪枝，第二种是低阶分解和低阶近似，第三种是网络量化和二值化。这篇文章的关注点在网络的二值化方法上。 

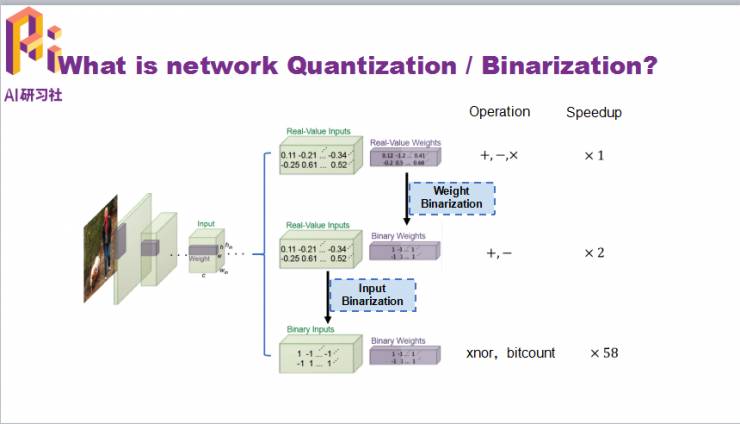
什么是网络的二值化/量化？这里以CNN的一个卷积层为例。

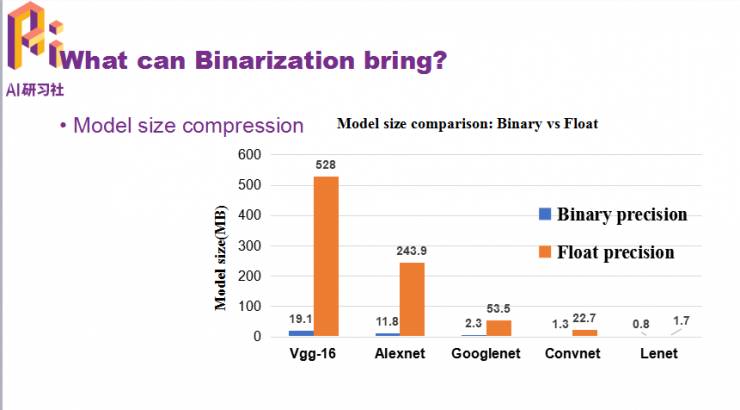
卷积层的二值化有两个优点，第一个优点是可以实现模型大小的压缩。

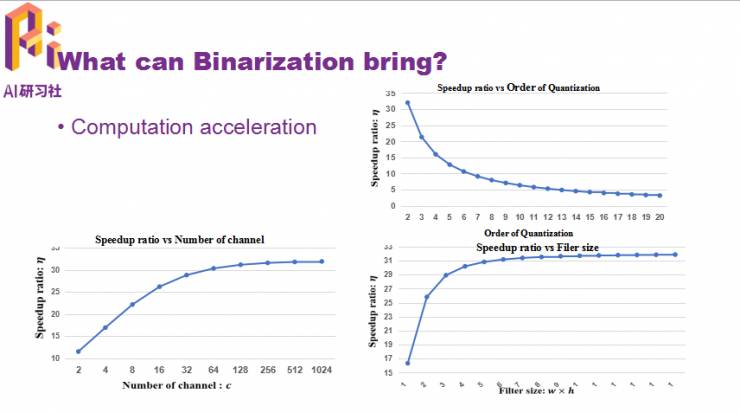
第二点是能加速计算。

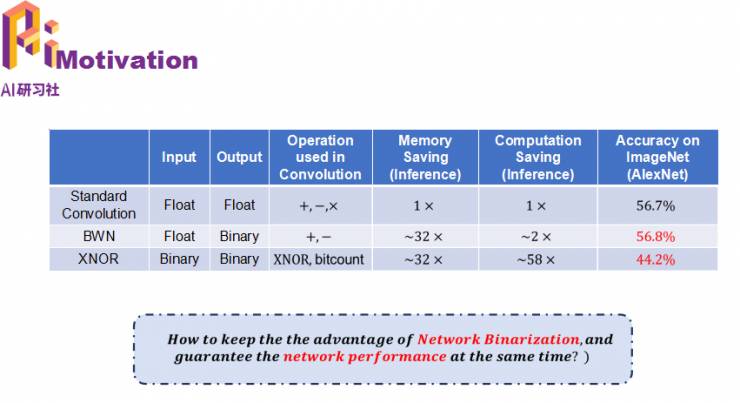
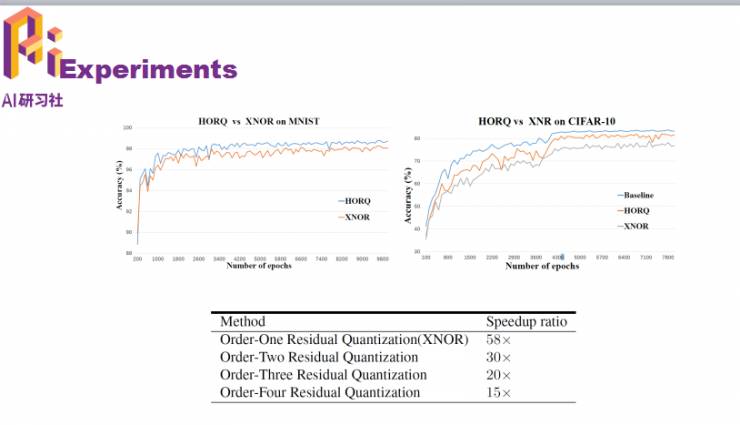
接下来介绍这篇文章的motivation，之前的XNOR网络虽然能实现58倍的加速，但网络精度出现大幅下降。我们希望既能利用二值化带来的便利，也避免网络精度的大幅度下降。

说到这篇文章的方法之前，我们再来看看如何进行网络二值化。由浅入深，先来谈谈如何进行向量二值化。

向量二值化的目标如下：

求解如下最小二乘估计：

相当于求解如下问题，可以转化为如何最大化X转置乘以H的问题。

求解完H之后再来求解β，求解过程如下：

由此得到前面图中该最优化问题的解析解形式如下：

下面举个例子，如何运用向量二值化来二值化向量的內积。如下是四维向量相乘的例子： 

求解X和W內积的式子如下所示：

估算值为1.27875，与实际值0.76相比有很大误差。这也表示，用这样的方法进行向量二值化会带来很大误差，信息损失巨大。 

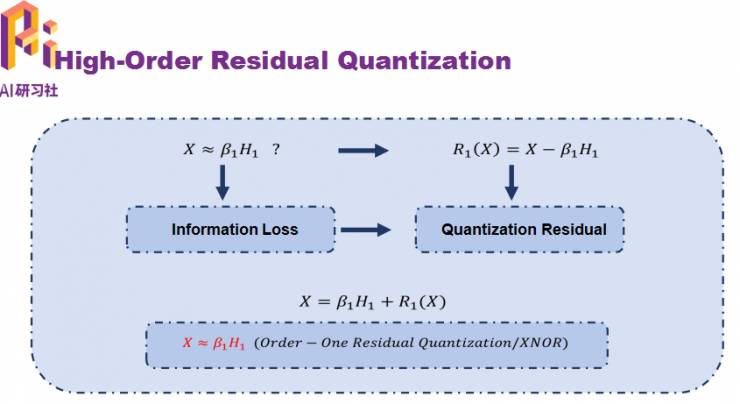
由此，我们的工作提出高阶残差量化，利用泰勒展开的方法，具体如下：

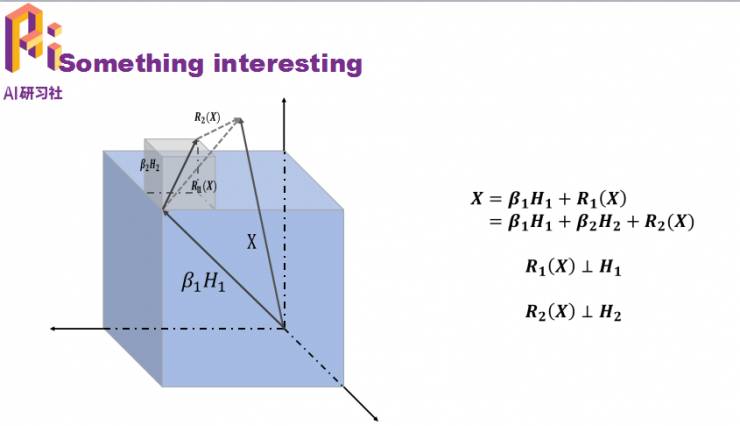
如图左所示是原来二值化方法的信息损失，我们定义量化残差的概念来描述信息损失：

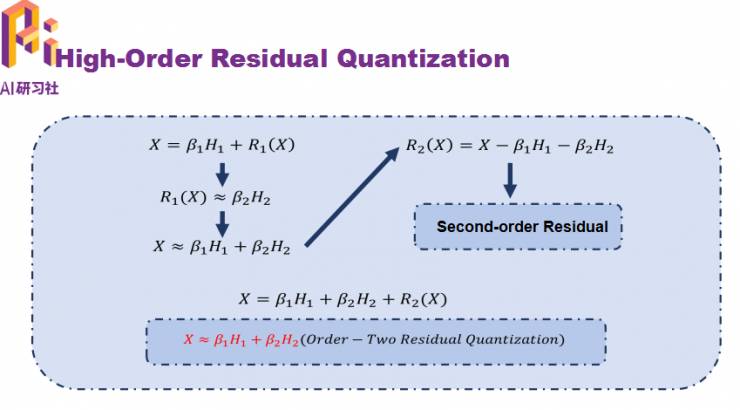
由此可以上升到二阶残差量化估计：

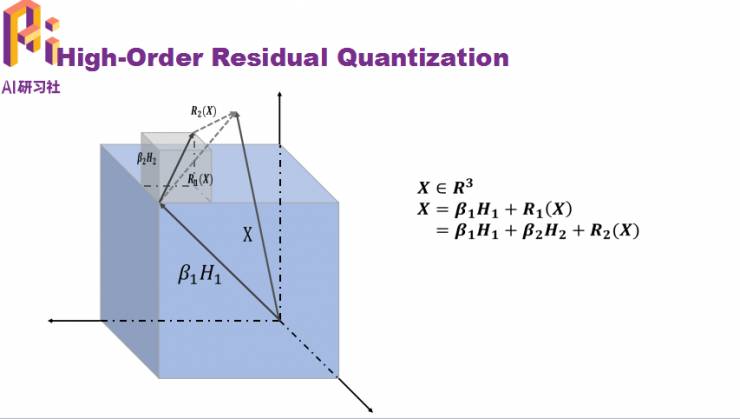
下面是从三维空间来看：

以此类推，我们可以定义K维残差估计：

接下来利用HORQ（高阶残差）方法来逼近我们刚才XW=0.76的例子：

下面求得X的二阶量化值，对W不用进行二阶二值估计，因为在之前网络中对权值进行二阶二值估计对网络的影响不是很大，我们只讨论对输入进行高阶残差估计方法。XW的值如下：

最后的结果如下：

同理作出三阶二值估计：

三阶量化的结果如下，在0.81左右。

同理可以做四阶二值估计，有一个很有意思的结论，对于n维向量X，它最多只有n阶二值估计。

把这些残差估计做一个汇总，如下：

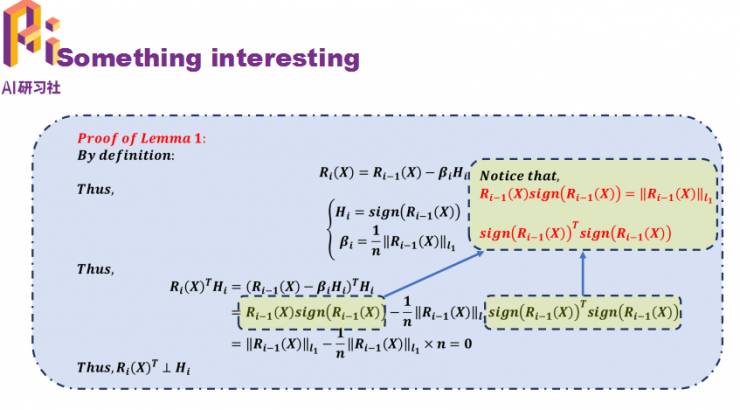
这是一些HORQ框架下理论上比较有趣的结果。结论一：二值的残差一定是跟相应阶数下的二值向量垂直。

推导过程如下，另外还有一些小结论：

下面这张图中可以应用上面推导出来的定理。

结论二：随着i的增加信息损失是逐渐减少的。

第三个结论如下图：

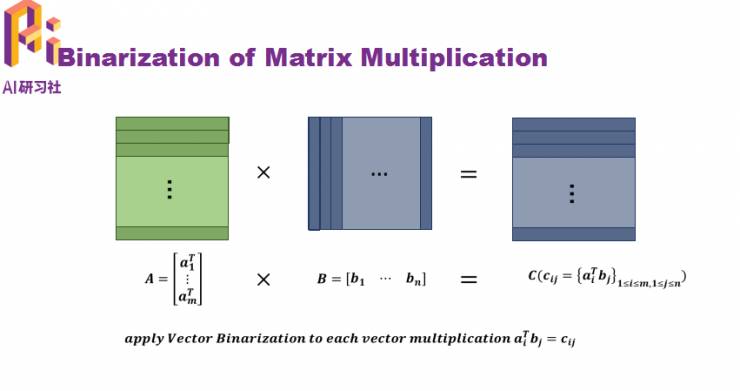
接下来讲一下如何将HORQ的方法应用到矩阵乘法中。

实际上矩阵乘法可以看成一个行向量和一个列向量的乘积。

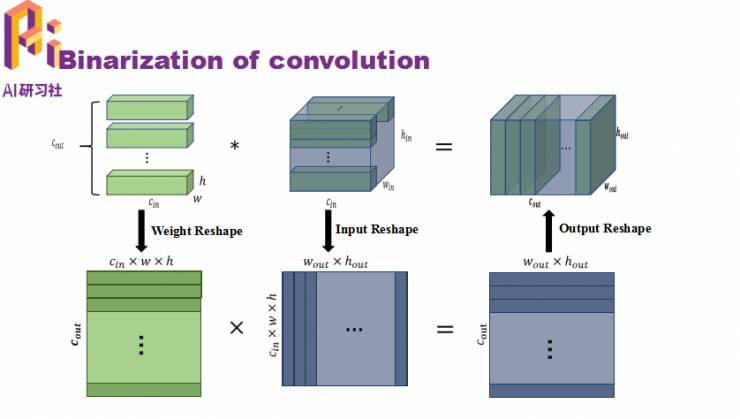
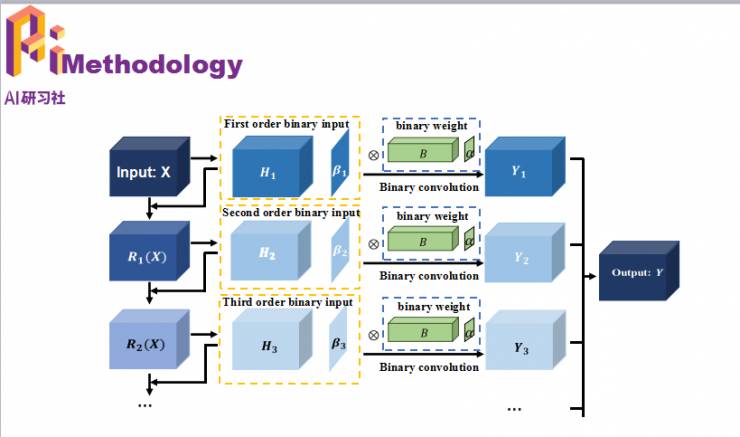
话说回来，如何利用HORQ的方法计算卷积层呢？

这里涉及到tensor reshape过程，具体的过程如下：

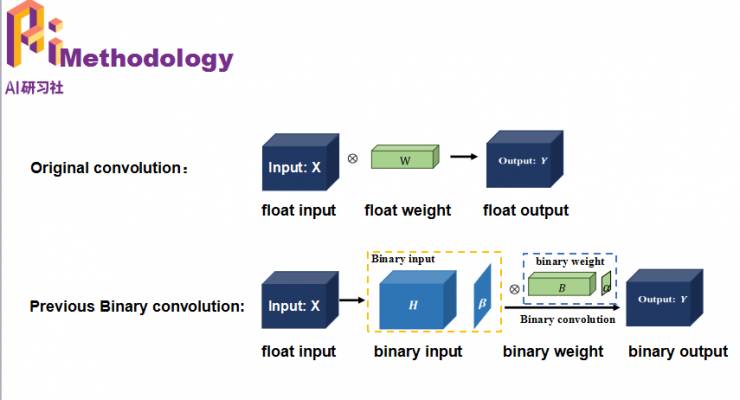
下面是原始的卷积网络以及对权值和输入二值化来进行卷积操作，这样带来的信息损失巨大。

HORQ提出了下面这样一个框架模型。

下面是一些实验结果，可以看到在一些小数据集上都有不错的表现，基本上可以降低一半的误差。图中也给出了不同阶数的加速比。

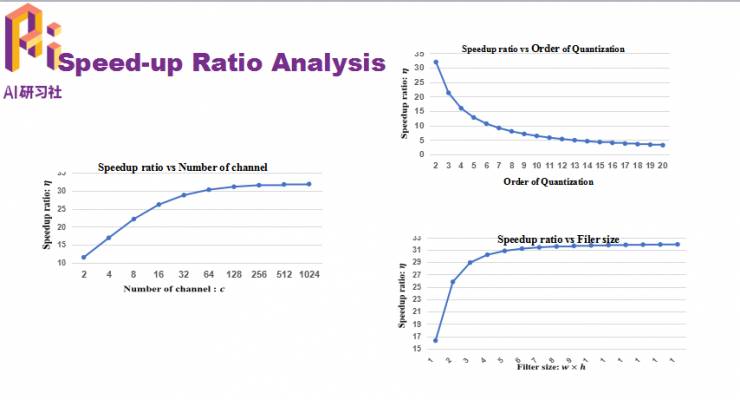
下面是加速比的一些理论分析，加速比与三个因素有关，公式如下：

可以看到参数之间的相关关系：

接下来是一些问题。实际上HORQ网络模型依赖于二值化矩阵乘法的计算，需要一些比较合适的框架，二值模型的存储和载入与浮点数的存储和载入不一样。

论文地址：https://arxiv.org/abs/1708.08687

本次分享的视频如下：

AI科级评论编辑整理。

—————  给爱学习的你的福利  —————

随着大众互联网理财观念的逐步普及，理财规模随之扩大，应运而生的智能投顾，成本低、风险分散、无情绪化，越来越多的中产阶层、大众富裕阶层已然在慢慢接受。王蓁博士将以真实项目带你走上智能投顾之路，详情请识别下图二维码或点击文末阅读原文～

————————————————————