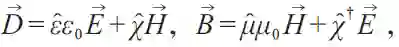能谷光子晶体与拓扑光传输
作者:汤国靖 陈晓东 董建文 (中山大学物理学院)

摘要 在传统光学原理框架下,高效光传输问题在集成光电子领域的发展受到了制约。人们希望从物理源头出发,提出新型原理机制或设计方法,来获得整体上的高保真光传输性能。这正好与近年兴起的拓扑光子学内涵相吻合。近年来,光子晶体和超构材料等多种电磁系统都被用于拓扑光子学的研究中,并受到了广泛关注。文章简要回顾拓扑光子学的发展历程,重点介绍能谷光子晶体的物理特性和最新研究进展,集中论述了电磁对偶能谷光子晶体的理论提出、能谷光子晶体分类与微波实验观测、硅基能谷光子晶体与光波段传输实现等方面。最后,将讨论该领域的未来,并展望其在微纳集成光子学领域的可能发展方向。
关键词 拓扑光子学,能谷光子晶体,光学量子(自旋/能谷)霍尔效应,光传输
大数据和下一代通信技术对数据计算、信息处理和传输速度的要求不断提高,新型光信息处理/传输的维度和自由度将成为后摩尔时代的关键技术核心。在传统光学原理框架下,高效光传输问题在集成光电子领域的发展受到了制约。例如,光在微纳光子器件中传输时因遇到大角度转弯、制备误差引起的缺陷和无序等被强烈散射,引起严重的散射损耗问题,从而影响了光子器件·的传输性能。人们希望从物理源头出发,提出新型抗散射机制来获得整体上的高保真光传输性能,这正好与近年兴起的拓扑光子学(Topological Photonics)内涵相吻合。
拓扑学是数学中的一个分支,主要研究几何图形或者空间在连续变化过程中还能保持不变的一些整体性质。拓扑学关注的是几何物体在连续形变下保持的全局性质,它只关注物体之间的位置关系而不考虑它们的大小和形状。早期,研究者利用能带理论,解释了凝聚态中量子霍尔效应[1]、量子反常霍尔效应[2]等现象。近年来,研究者进一步将拓扑方法引入到光学和声学的研究中,发现了诸如宽带单向传输、抗散射传输等新型传输现象[3—7]。同时,对于拓扑光学结构而言,缺陷和无序只会引起局部参数变化,不影响该光学结构的全局性质。因此,拓扑光学结构的光子态的性质非常稳定,对微纳制备误差有较高的容忍度。
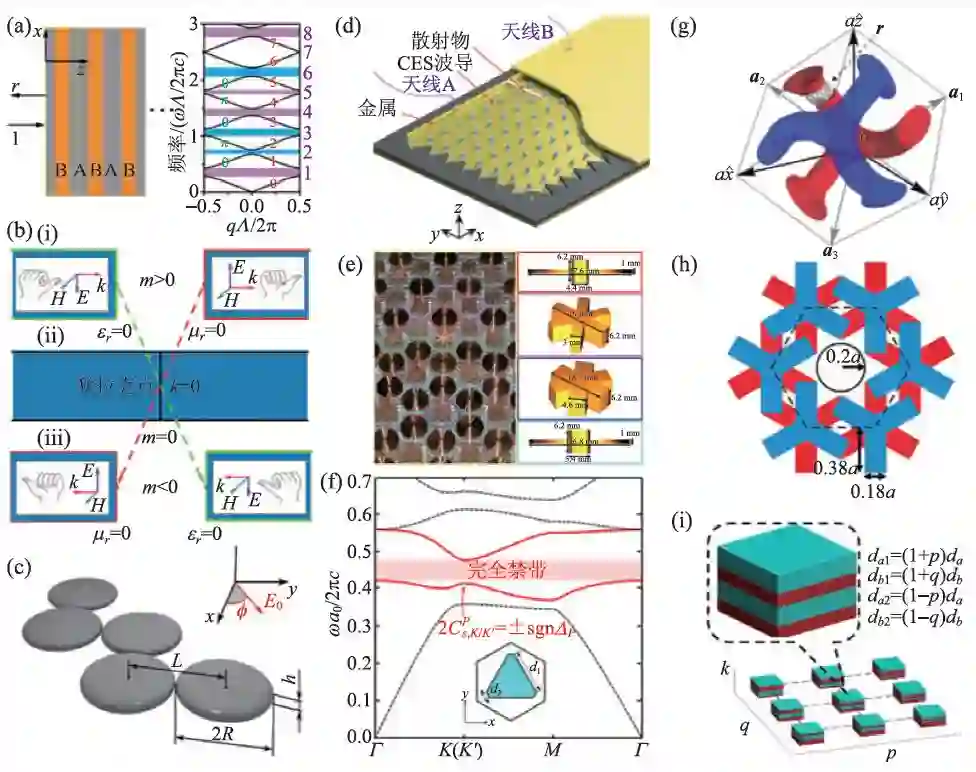
在光学领域,拓扑理论在一维系统、二维系统和三维系统中均有所运用,如图1 所示。一维光学系统的拓扑性质研究集中在对Su—Schrieffer—Heeger 模型中的扎克相位(Zak phase)讨论[8—10]。例如,香港科技大学研究者指出一维光子晶体体能带的扎克相位与光子晶体表面的光学阻抗之间的内在联系,发现一维光子晶体态模式会随着组分材料占空比改变而发生交换。两个扎克相位不同的一维光子晶体并排放置的界面支持零维局域模式[8]。同济大学研究者将麦克斯韦方程组对应到一维狄拉克方程,以此建立了拓扑态与电磁波手性模式之间的关系。通过微波实验,他们报道了与电磁波手性模式交换相关的能带翻转[9]。俄罗斯科学院研究者则提出一种表面等离激元微粒锯齿形链结构,通过将该结构中的耦合偶极子方程对应到超导体研究中的Bogoliubov—de Gennes 方程,用表面等离激元模拟了马约拉纳费米子,并通过改变入射光的偏振方向选择性激发局域在锯齿形链两末端微粒处的表面等离激元模式[10]。由于该锯齿状链结构易于微纳制备,最近已被用于实现拓扑光激射[11]。
图1 (a)一维光子晶体与其能带结构。图中标出了每条能带的扎克相位[8];(b)一维超构材料的拓扑相变与手性模式交换;(c)实现拓扑马约拉纳态的锯齿状表面等离激元微纳颗粒示意图[10];(d)光学类量子霍尔效应的磁性光子晶体实验示意图[9];(e)实现光学类量子自旋霍尔效应的超构材料波导示意图[30];(f)实现光学类量子能谷霍尔效应的全硅能谷光子晶体原胞示意图与能带结构[35];(g)具有光子外尔点的三维螺旋光子晶体的原胞示意图[12];(h)具有高拓扑荷光子外尔点的光子晶体原胞示意图[14];(i)通过引入人工维度在参数空间中得到外尔点的一维光子晶体的原胞示意图[18]
外尔点(Weyl point)是三维K空间中的能量简并奇点,在该能量奇点附近能带呈现出线性色散,且在三维K 空间中产生非零贝里曲率(Berrycurvature)。光学系统中的外尔点已在三维光子晶体中被发现[12—18]。例如,麻省理工学院研究者提出一种全电介质三维螺旋光子晶体,当空间反演对称性或时间反演对称性被破坏时,会出现频率隔离的外尔点。进一步,还证明了该外尔三维光子晶体的表面支持无能隙的表面态[12]。通过对高折射率陶瓷进行精确钻孔,他们实验制备了该三维螺旋光子晶体,并通过微波实验测量了方向透射谱线,验证了外尔点的存在[13]。有别于全电介质材料,香港科技大学研究者则利用堆叠印刷电路板设计了一种多层平板光子晶体,该光子晶体支持具有拓扑荷为2 和3 的外尔点。通过微波实验,他们验证了表面态的抗散射性质[14]。此外,磁化表面等离激元[15]和螺旋光波导[16]中的第二类外尔点、光子晶体中受结构对称性保护的理想外尔点[17]、人工维度参数空间中的外尔点[18]等相关研究也逐步引起了人们的关注。另一种三维拓扑光学结构是三维光拓扑绝缘体。三维光拓扑绝缘体具有三维全向禁带,对于频率落在禁带范围内的光在晶体内部沿各个方向都无法传输。实现三维光拓扑绝缘体有助于深入挖掘拓扑物理并发掘其在光子器件中的应用[19—21]。麻省理工学院研究者设计了一种旋电材料组成的三维光拓扑绝缘体,该结构支持单一表面狄拉克锥及其无带隙表面态[19]。又如,浙江大学研究者实验实现了一种宽带隙三维光拓扑绝缘体,通过微波测量观测到具有带隙的体态能带、具有狄拉克锥状的线性色散表面态、抗散射传输的表面态[20]。
二维系统相对于一维系统,可以调控的物理量更为丰富,相对于复杂三维系统,实验制备相对简单;加上与集成光电子器件研发方向高度匹配,是目前较有优势的拓扑光学平台。二维拓扑光学系统,按照拓扑性质可分为光学类量子霍尔系统(Photonic Quantum Hall System)、光学类量子自旋霍尔系统(Photonic Quantum Spin Hall System)和光学类量子能谷霍尔系统(Photonic Quantum Valley Hall System)。普林斯顿大学研究者提出使用具有法拉第效应的材料打破时间反演对称性,在三角格子光子晶体中实现光学类量子霍尔效应[22]。2009 年,麻省理工学院研究者在四方格子磁性光子晶体中探测到了单向抗散射的拓扑保护边界态,实验证实了光学类量子霍尔效应[23]。随后,南京大学研究者在六方格子磁性光子晶体中进一步探测到了光子晶体与空气之间的单向抗散射传输边界态[24]。磁性光子晶体使用磁性材料且需要外加磁场,实际上不使用磁性材料同样可以实现光学类量子霍尔效应。2012 年,斯坦福大学研究者指出,在谐振腔阵列中对相邻谐振腔耦合系数在时间上进行周期性调制产生等效磁场,可实现光学类量子霍尔效应[25]。以色列工学院研究者则使用螺旋波导阵列结构,以在光传播方向上对波导进行周期性调制充当“时间”调制,通过光学实验验证了该结构支持单向传输的抗散射边界态[26]。
除了光学类量子霍尔效应,光学类量子自旋霍尔效应也被广泛地研究。电子是自旋为1/2 的费米子,而光子与之不同,是自旋为1 的玻色子。为了类比电子的自旋,需要引入光子“赝自旋”。例如,马里兰大学研究者使用耦合环形谐振腔波导阵列中光在环形谐振腔内顺时针与逆时针方向传播的两种模式作为赝自旋,通过调整相邻谐振腔的耦合系数,获得了拓扑保护赝自旋边界态[27]。进一步,南洋理工大学研究者将环形谐振腔结构应用于人工表面等离激元结构,通过引入多种常见缺陷,在数值模拟和微波实验上讨论了赝自旋边界态所免疫的缺陷种类[28]。除此之外,如果能在光子晶体或超构材料等人工光学结构中实现不同模式的简并,就可以通过简并模式间组合构造出赝自旋。例如,在介电常数/磁导率匹配的超构材料中可使用同相/反相横电模(transverse electric mode,i.e.,TE mode)和横磁模(transverse magnetic mode,i.e.,TM mode)作为一对赝自旋[29,30],在压电、压磁材料堆叠柱构成的光子晶体中以左旋偏振态和右旋偏振态作为赝自旋[31]。除了这种在整条能带上TE 与TM模都简并的完全简并情况,也可以设计出仅在一定频率或波矢范围内TE 与TM 模式偶然简并的光子晶体。德克萨斯大学奥斯汀分校研究者设计了一种金属平板夹柱体结构的光子晶体,其TE 与TM 模式在布里渊区边界附近简并,从而实现以同相/反相TE—TM 模式为赝自旋的光学类量子自旋霍尔效应[32]。中山大学研究者通过调控各向异性介电常数张量实现了TE 与TM模式的偶然简并,并通过引入双各向异性耦合系数获得拓扑非平庸禁带[33]。此外,日本材料科学国家研究中心研究者则考虑六方格子电介质光子晶体,利用折叠原胞的方式实现了布里渊区中心的双重简并狄拉克锥。通过扩展与收缩原胞获得带隙自旋陈数不同的两种光子晶体,并实现了其边界态的抗散射传输[34]。
光学类量子霍尔效应系统打破时间反演对称性,能够产生单向传输的边界态。光学类量子自旋霍尔系统中赝自旋态互不耦合且传输方向相反,因此赝自旋态具有单向传输性质。为了实现更多样的光场调控,进一步降低实现拓扑非平庸态对材料性质和外加条件的要求,一种新的自由度——能谷自由度被引入到光子晶体中,下面我们将简要回顾能谷光子晶体的研究历程。
蜂窝状结构是能谷光子晶体的一种常用结构,为了使蜂窝状光子晶体的能带在不同能谷(布里渊区边界上能带的极值点)具有不同性质,需要打破结构的空间反演对称性。这里,先讨论不依赖于偏振的电磁对偶能谷光子晶体。如上节所述,为了满足电磁对偶条件,需要实现模式简并,该模式简并可以通过完全简并或偶然简并实现。中山大学研究者讨论了严格简并的电磁耦合能谷光子晶体,其组成材料的物质方程为[36]
其中χ̂ 是双各向异性张量。为了满足电磁对偶条件,介电常数与磁导率的比值为恒值,即ε̂/μ̂为常数。为了打破结构的空间反演对称性,蜂窝状光子晶体的原胞中不同圆柱的双各向异性张量相反,则可以通过相反的开口环方向实现(图2(a))。数值模拟计算表明,两种赝自旋体态能带在K'和K 能谷发生劈裂。而且该赝自旋劈裂依赖能谷,即在K'能谷处赝自旋向上态频率比赝自旋向下态频率高,相反在K能谷处赝自旋向下态频率比赝自旋向上态频率高。通过分析体态的等频线,发现K'能谷的赝自旋向上态只沿ΓK'方向传输,而K能谷的赝自旋向下态只沿ΓK方向传输。因此,如图2(a)所示,两能谷的不同赝自旋态沿不同方向传输,从而实现了赝自旋与能谷锁定的体态传输,即光学能谷霍尔效应。同时,该电磁对偶光子晶体的陈数、自旋陈数、能谷陈数均为零,说明了该光子晶体的平庸拓扑性质,但它同样支持赝自旋能谷锁定体态传输。此外,他们也讨论了自旋陈数非零的电磁对偶能谷光子晶体,通过对双各向异性系数的调控,可以实现接近平带的边界态色散曲线。为了结合能谷自由度进行更多样化的光场调控,还引入频率自由度在光子晶体波导中分别实现频率调控的能谷霍尔效应、基于赝自旋的隔离器原型设计[37]。
图2 (a)电磁对偶能谷光子晶体中的光学赝自旋—路径关联传输[36];(b—g)具有光学量子自旋霍尔、量子霍尔、量子能谷霍尔效应的光子晶体原胞结构示意图和对应体能带[38]
以上电磁对偶能谷光子晶体的实现需要满足介电常数与磁导率比值恒定的条件,对材料要求较为苛刻。在布里渊区边界上实现模式的偶然简并同样可以实现电磁对偶能谷光子晶体。德克萨斯大学奥斯汀分校研究者提出金属平板夹柱体的结构可实现TE 与TM模的偶然简并[32]。如图2(b)所示,通过打破结构z 方向的镜像对称性引入等效双各向异性张量,得到了自旋陈数非零的量子自旋霍尔光子晶体(图2(e))。类似的结构也可以用于实现电磁耦合能谷光子晶体[38]。如图2(d)所示,他们通过将原胞中的圆柱替换为Y形柱,打破了空间反演对称性,从而打开双重简并的狄拉克锥,获得能谷陈数非零的量子能谷霍尔光子晶体(图2(g))。此外,如图2(c)所示,如果通过引入磁性材料打破时间反演对称性,可以获得陈数非零的量子霍尔光子晶体(图2(f))。
电磁对偶能谷光子晶体需要通过调整材料参数或者结构参数获得简并模式,这给光子晶体设计带来一定的限制。其中,严格简并电磁对偶光子晶体往往需要使用超构材料实现,其结构复杂,难以在光学波段应用。在偶然简并电磁对偶光子晶体的实验研究方面,新加坡南洋理工大学研究者基于金属板夹柱体结构,不仅观测到了抗散射传输的双偏振边界态,还实现了边界态近乎完美的出射耦合[39]。但是偶然简并电磁对偶光子晶体所用的金属材料在光波段吸收较大,同样只适用于微波等长波段。为了去除模式简并条件的限制,可以考虑单偏振能谷光子晶体。
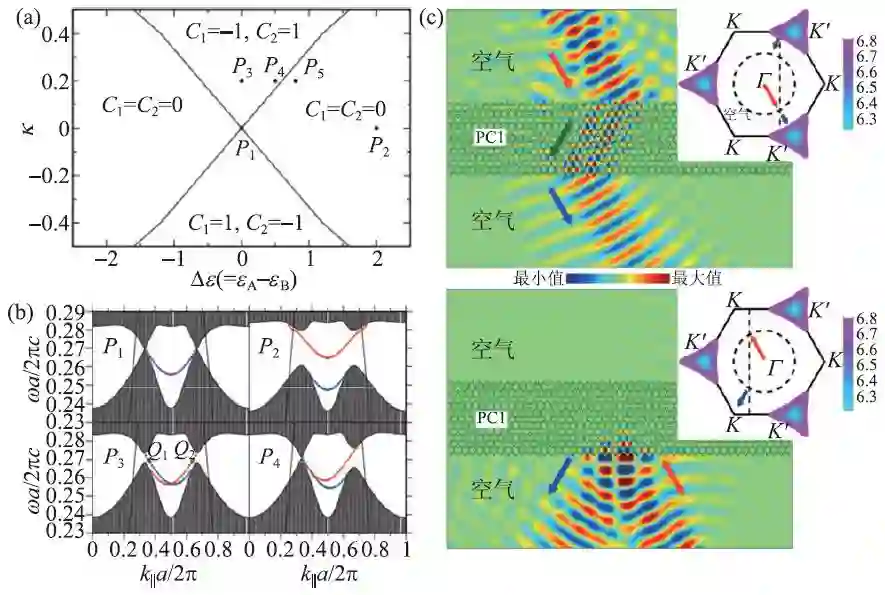
实际上,在拓扑光子系统中能谷自由度被广泛研究之前,研究者已在量子霍尔光子晶体中讨论空间反演对称性破缺的情况。2009 年,日本国家材料科学研究所和秋田大学研究者讨论了同时打破时间反演和空间反演对称性的磁性光子晶体,通过改变蜂窝状光子晶体原胞中不同柱体的介电常数来打破空间反演对称性[40]。随后在2012年,日本国家材料科学研究所研究者使用等效哈密顿量对这种蜂窝状光子晶体进行了更详细的分析[41]。如图3(a)所示,当原胞中两圆柱的介电常数差值超过一定限度时,光子晶体原本非零的陈数会变为零,即发生拓扑相变。如图3(b)所示,两种拓扑相光子晶体具有不同的边界态色散曲线,其中光学量子霍尔光子晶体边界态色散穿过整个带隙,而陈数为零的光子晶体的边界态则会在进入带隙后又回到原来的能带[40]。
图3 (a)蜂窝状磁性光子晶体关于两圆柱介电常数差和磁性系数的拓扑相图[40];(b)时间反演对称性破缺的能谷光子晶体边界态色散曲线,红色与蓝色曲线对应不同的边界,P1,P2,P3,P4 对应(a)中不同光子晶体[40];(c)时间反演对称性破缺的能谷光子晶体实现体态负折射与单向传输,插图为等频线图和体态传输方向示意图[42]
前期关于蜂窝状磁性光子晶体的研究并没有关注能谷自由度。研究表明,当空间反演对称性破缺性占主导作用时,虽然光子晶体的陈数为零,但其能谷陈数非零,属于光学量子能谷霍尔拓扑相[42,43]。也就是说,时间反演对称性破缺程度与空间反演对称性破缺程度存在一种类似“竞争”的关系,通过改变两种对称性被打破的程度,可以使光子晶体在光学量子霍尔相与光学量子能谷霍尔相两种拓扑相之间发生相变。上述这两类光子晶体的边界态具有不同的抗散射性质,陈数相反的两个光子晶体之间的边界支持单向传输边界态,对截断边界的散射体免疫。另一方面,能谷陈数相反的两个光子晶体之间能谷依赖的边界态,即边界态的群速度在两能谷相反。这种边界态对于垂直插入边界的散射体并不免疫[42],但是仍然可以在120°大角度转弯中实现抗散射传输[43]。最后,我们也需要注意到,当同时打破时间反演和空间反演对称性时,无论处于哪种拓扑相,体态能带在两能谷处有不同的极值频率,即两能谷对应带隙大小不同,这为实现单向体态传输提供了条件[42,44]。如图3(c)所示,时间反演对称性破缺的单偏振能谷光子晶体可用于实现体态负折射和单向传输。
上述时间反演对称性破缺的能谷光子晶体虽然不需要模式简并,但仍需要打破时间反演对称性,因此需要使用磁性材料,实验时需要施加磁场。由于光频段磁性材料的缺失,时间反演对称性破缺的能谷光子晶体同样难以在光频段实现。实际上,只打破空间反演对称性而保持时间反演对称性,同样可以实现光学类量子能谷霍尔效应。2016 年,德克萨斯奥斯汀分校研究者提出了一种全电介质能谷光子晶体[35]。他们考虑TE 模式,在能谷陈数相反的光子晶体构成的边界上发现了能谷依赖边界态,并指出在空间反演对称性破缺下边界态的拓扑保护需要抑制能谷间散射。发现当能谷间散射被抑制时,所激发的边界态具有较高的出射效率。如图4(a)所示,当出射截面与边界呈60°角时,边界态具有较高的出射效率,而当出射截面与边界呈90°角时,边界态会发生较强的背向散射。中山大学研究者进一步在理论上研究了全电介质能谷光子晶体的拓扑性质,通过对TM模式的分析指出,位于不同能谷的体态的电场局域相反的涡旋相位,因此通过控制激发源的相位涡旋旋性可实现能谷体态的选择性激发。而且,如图4(b)所示,数值模拟表明能谷陈数相反的能谷光子晶体之间的边界态在120°转弯过程中具有抗散射传输性质[45]。只要能谷间散射被抑制,整个禁带内边界态均具有抗散射传输性质。表面等离激元晶体中也可以实现光学类量子能谷霍尔效应,例如华侨大学研究者提出,控制类石墨烯表面等离激元光子晶体微盘半径和等效势场两种方法打破空间反演对称性,从而构造出能谷表面等离激元光子晶体[46]。
图4 (a)出射截面形貌对于能谷光子晶体边界态出射的影响[35];(b)能谷光子晶体边界态在Z型波导的抗散射传输[45];(c)人工表面等离激元晶体中拓扑保护边界态的近场扫描结果(左)和场分布的傅里叶变换(右)[47];(d)表面波光子晶体中的分离波束,插图为两能谷体态电场相位涡旋旋性示意图[48];(e)微波实验结果表明,当左手相位涡旋激发源(左侧)改变成右手相位涡旋激发源(右侧)时,出射到空气中的光束由只从左侧端口出射变成只从右侧端口出射[50]
由于结构简单,材料参数不苛刻,研究者很快在微波频段实现了时间反演对称的单偏振能谷光子晶体。例如,重庆大学研究者在人工表面等离激元晶体中用近场扫描方法直接观测到拓扑保护的边界态(图4(c)),通过对边界态场分布的傅里叶分析验证了沿某个方向传播的边界态只会在特定能谷附近激发[47]。近场扫描测量技术也被用于能谷光子晶体体态传输的探测,新加坡南洋理工大学研究者观测到沿ΓM方向入射的波束分裂成两束沿不同方向传输的波束,实现了光束分离[48]。同时,他们还证实了不同波束上电场具有不同的涡旋相位(图4(d))。同样是体态激发,武汉大学和苏州大学研究组使用的是置于光子晶体内部的手性激发源,通过控制激发源各天线之间的相位差可实现能谷体态激发[49]。中山大学研究者则使用三个偶极天线作为激发源,通过改变偶极天线的初相位,使激发源从左手涡旋相位逐渐向右手涡旋相位转变[50]。由于不同的输入源涡旋相位激发位于不同能谷的体模式,因此最终出射到空气中的光束会由只从左边端口出射转变成只从右侧端口出射(图4(e))。通过将不同能谷陈数的能谷光子晶体放置在一起形成边界,获得了横跨整个禁带的能谷依赖边界态。并通过直波导和120°转弯波导的透射谱线和近场扫描成像证明了边界态的宽带抗散射传输行为。他们还发现,光子晶体与理想电导体之间同样存在能谷依赖边界态。通过调整边界形貌(如改变边界陶瓷柱直径、边界陶瓷柱与理想电导体间距)对边界态色散曲线进行调控,实现平带边界态到无带隙边界态的演变,该可调边界态色散曲线有望用于实现透射带宽可调的光子器件[50]。
尽管关于能谷光子晶体已有大量研究,但由于物理原理或材料属性等方面的限制,大多数仍集中在宏观尺度样品和微波工作频段,难以直接推广到微纳尺度光学频段,制约了拓扑光子学与微纳光子学之间的融合发展。为了将能谷光子晶体的工作频段推广至光通讯区乃至可见光,可以选取的材料参数相对有限,材料的磁导率和双各向异性耦合系数均取零,能够调整的参数为介电常数,这给微纳能谷光子晶体的设计带来了难度。幸运的是,虽然材料参数的选择比较有限,但可以通过调整光子晶体中介电常数的空间分布获得能谷陈数非零的非平庸拓扑光子系统[51—54]。例如,宾夕法尼亚大学研究者研究耦合波导阵列,通过使原胞内两波导的折射率不同(图5(a)),在红外波段观测到了光学类量子能谷霍尔效应中的拓扑保护边界态。实验中,他们验证了边界态出现在锯齿状边界而非靠椅状边界[51]。
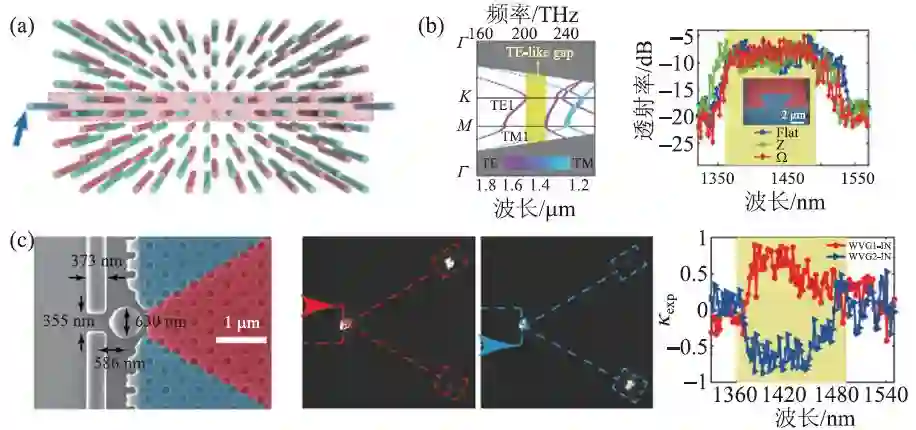
图5 (a)基于耦合波导阵列的能谷光学系统示意图[51];(b)SOI 能谷光子晶体平板能带结构(左)和不同形态光波导的透射光谱(右),插图为Ω形光波导的扫描电镜图[53];(c)使用绝缘层硅光子晶体平板设计光子拓扑路由的扫描电镜图(左)、依赖于入射光方向的SOI 拓扑光子路由远场成像实验结果(中)、实验测量透射分光比谱线图(右)[53]
相比耦合波导阵列,在微纳平板(如SOI)中实现片上能谷光子晶体更有望推进拓扑光子学与微纳光子学的深入融合,为新型集成光子结构及其器件原型的设计提供指导原理。最近,这种硅基系统的边界态激发被美国研究者[52]和中山大学研究者[53]分别实现。中山大学研究者利用能谷—赝自旋耦合原理,在绝缘层硅(siliconon-insulator,SOI)上制备出能谷光子晶体平板。该能谷光子晶体平板具有约40 nm 的特征尺寸,如图5(b)所示,其光子模式(位于光锥以下)能够较好地局域在平板内,抑制了平板外损耗,且在光通信波段具有TM模式带隙。实验中,研究者制备了直线形、Z 形和Ω形三种光波导,测量出高透平顶透射光谱带,证实了近红外波段下拓扑保护的宽带边界态抗散射传输。进一步,他们采用硅微盘方案产生相位涡旋源,如图5(c)所示,借助于非均匀光栅的垂直耦合,在光学显微镜下观察到了拓扑边界态的选择性激发实验结果:当入射光从上端/下端波导进入时(红色/蓝色箭头),光场在波导微盘中产生逆时针/顺时针相位涡旋,大多数能量耦合到沿右上方/右下方传播的拓扑边界态。从透射分光比谱线可以看出,这种边界态的选择性耦合可在几十纳米的光学带宽内实现。本工作在无需低温和强磁等极端环境下,实现了亚微米量级耦合长度的宽带光子路由行为,并在硅基平台上验证了能谷—赝自旋耦合等拓扑光学原理[53]。
拓扑光子学突破了过去单一自由度进行光场调控的传统框架,通过聚焦诸如电磁对偶、横向自旋、光子能谷等多自由度耦合的多维度调控新机制,实现赝自旋单向传输、边界态抗散射传输等新型光传输行为。为将拓扑光子学的理论应用到微纳光子学研究,促进拓扑光子学与微纳光子学之间的融合发展,并为高效光信息传递、光电信息处理等重大需求提供基础性和前瞻性技术储备,需着力研究微纳拓扑光子学。这一方面要求我们从基础理论层面进一步挖掘更多适用于微纳系统的非平庸拓扑相。例如通过引入层自由度研究双层结构[55—57],可以实现比单层结构更丰富的拓扑相。特别的是,微纳尺度的全电介质双层光子晶体平板已被理论提出[55],通过不同拓扑相双层结构的拼接有望实现光场在层间高效切换[56]。又如研究高阶光子晶体,通过反常的体边界对应关系在二阶拓扑光子晶体中寻找受拓扑保护的零维角模式[58—61]。由于角模式的场分布可以较好地局限在角落,有利于增强光与物质的相互作用。另一方面,借鉴拓扑光子学理论,结合微纳光学系统的特有性质,实现新型光场调控。研究动态可调的光子晶体,以实现高速调制光子器件[62]。结合光学材料的增益和损耗性质,探索非厄米光学系统的拓扑属性,研究非厄米光子晶体中边缘态与拓扑数间的关系,继而揭示非厄米光学系统中抗散射行为的新物理机制。此外,由于缺乏近场成像和超快光谱学的成套分析方法,微纳拓扑光子学研究还将遇到模式表征困难、瞬态响应过程分析缺乏等问题。为此,开发超高时空分辨的近场全光谱分析系统,研究光波导在极端时间和空间尺度下的瞬态动力学行为,也是非常必要的。
聚焦微纳拓扑光子学这一研究方向,挖掘更多适用于微纳系统的非平庸拓扑相,揭示拓扑光学系统中光传输、光与物质相互作用的新规律,为微纳光学与光子学、光二极管等关键光子芯片器件、混合集成光子学、高保真光量子信息光学、非线性光学等领域,提供新方法和新思路。
参考文献
[1] Thouless D J et al. Phys. Rev. Lett.,1982,49:405
[2] Haldane F D. Phys. Rev. Lett.,1988,61:2015
[3] Lu L et al. Nature Photonics,2014,8:821
[4] Khanikaev A B,Shvets G. Nature Photonics,2017,11:763
[5] Sun X C et al. Progress in Quantum Electronics,2017,55:52
[6] Xie B Y et al. Opt. Express,2018,26:24531
[7] Ozawa T et al. Reviews of Modern Physics,2019,91:015006
[8] Xiao M et al. Phys. Rev. X,2014,4:021017
[9] TanWet al. Sci. Rep.,2014,4:3842
[10] Poddubny A et al. ACS Photonics,2014,1:101
[11] St-Jean P et al. Nature Photonics,2017,11:651
[12] Lu L et al. Nature Photonics,2013,7:294
[13] Lu L et al. Science,2015,349:622
[14] ChenWJ et al. Nat. Commun.,2016,7:13038
[15] GaoWet al. Nat. Commun.,2016,7:12435
[16] Noh J et al. Nature Physics,2017,13:611
[17] Yang B et al. Science,2018,359:1013
[18]Wang Q et al. Phys. Rev. X,2017,7:031032
[19] Lu L et al. Nature Physics,2016,12:337
[20] Yang Y et al. Nature,2019,565:622
[21] Slobozhanyuk A et al. Nature Photonics,2016,11:130
[22] Haldane F D,Raghu S. Phys. Rev. Lett.,2008,100:013904
[23]Wang Z et al. Nature,2009,461:772
[24] Poo Y et al. Phys. Rev. Lett.,2011,106:093903
[25] Fang K et al. Nature Photonics,2012,6:782
[26] Rechtsman M C et al. Nature,2013,496:196
[27] Hafezi M et al. Nature Physics,2011,7:907
[28] Gao F et al. Nat. Commun.,2016,7:11619
[29] Khanikaev A B et al. Nat. Mater.,2013,12:233
[30] ChenWJ et al. Nat. Commun.,2014,5:5782
[31] He C et al. Proc. Natl. Acad. Sci. USA,2016,113:4924
[32] Ma T et al. Phys. Rev. Lett.,2015,114:127401
[33] Chen X D et al. Laser & Photonics Reviews,2018,12:1800073
[34]Wu L H,Hu X. Phys. Rev. Lett.,2015,114:223901
[35] Ma T,Shvets G. New Journal of Physics,2016,18:025102
[36] Dong JWet al. Nat. Mater.,2017,16:298
[37] Chen X D et al. Phys. Rev. B,2018,97:184201
[38] Ma T,Shvets G. Phys. Rev. B,2017,95:165102
[39] Gao F et al. Nature Physics,2017,14:140
[40] Ochiai T,Onoda M. Phys. Rev. B,2009,80:155103
[41] Ochiai T. Phys. Rev. B,2012,86:075152
[42] Lu J C et al. Journal of Optics,2018,20:075103
[43] Chan H C,Guo G Y. Phys. Rev. B,2018,97:045422
[44] Poo Y et al. Sci. Rep.,2016,6:29380
[45] Chen X D et al. Phys. Rev. B,2017,96:020202
[46] Qiu P et al. Journal of Physics D:Applied Physics,2019,52:015102
[47]Wu X et al. Nat. Commun.,2017,8:1304
[48] Gao Z et al. Phys. Rev. B,2017,96:201402
[49] Ye L et al. Appl. Phys. Lett.,2017,111:251107
[50] Chen X D et al. Phys. Rev. Appl.,2018,10:044002
[51] Noh J et al. Phys. Rev. Lett.,2018,120:063902
[52] Shalaev M I et al. Nat. Nanotechnol.,2019,14:31
[53] He X T et al. Nat. Commun.,2019,10:872
[54] Collins M J et al. Phys. Rev. A,2016,94:063827
[55] Chen X D,Dong JW. arXiv preprint,arXiv:1812.09169
[56]Wu X,Li Z,Chen J et al. arXiv preprint,arXiv:1812.06198
[57] Lu J et al. Phys. Rev. Lett.,2018,120:116802
[58] Peterson CWet al. Nature,2018,555:346
[59] Xie B Y et al. Phys. Rev. B,2018,98:205147
[60] Chen X D et al. Phys. Rev. Lett.,accepted. arXiv preprint,arXiv:1812.08326
[61] Ota Y et al. arXiv preprint,arXiv:1812.10171
[62] Dobrykh D A et al. Phys. Rev. Lett.,2018,121:163901
本文选自《物理》2019年第6期
3.现实中的“降维攻击”导致二维拓扑量子物态 | 文小刚点评
5.特别二的物理学——节选自《物理学咬文嚼字》彩色四卷本全集
10.周光召先生与开放的中科院理论物理所 | 贺周光召先生从事科学事业65周年