最新《非光滑优化》十讲硬核课程，剑桥大学梁经纬博士主讲

本课程主要包括非光滑优化和一阶近似分裂方法的主题。这包括基于梯度的方法(子梯度法、近端梯度法、加速梯度法)、算子分裂方法(增广拉格朗日法、乘子交替方向法、单调算子和算子分裂格式)和(可能的)内点算法。还将介绍非凸优化和随机优化。

https://jliang993.github.io/teaching

目录内容：

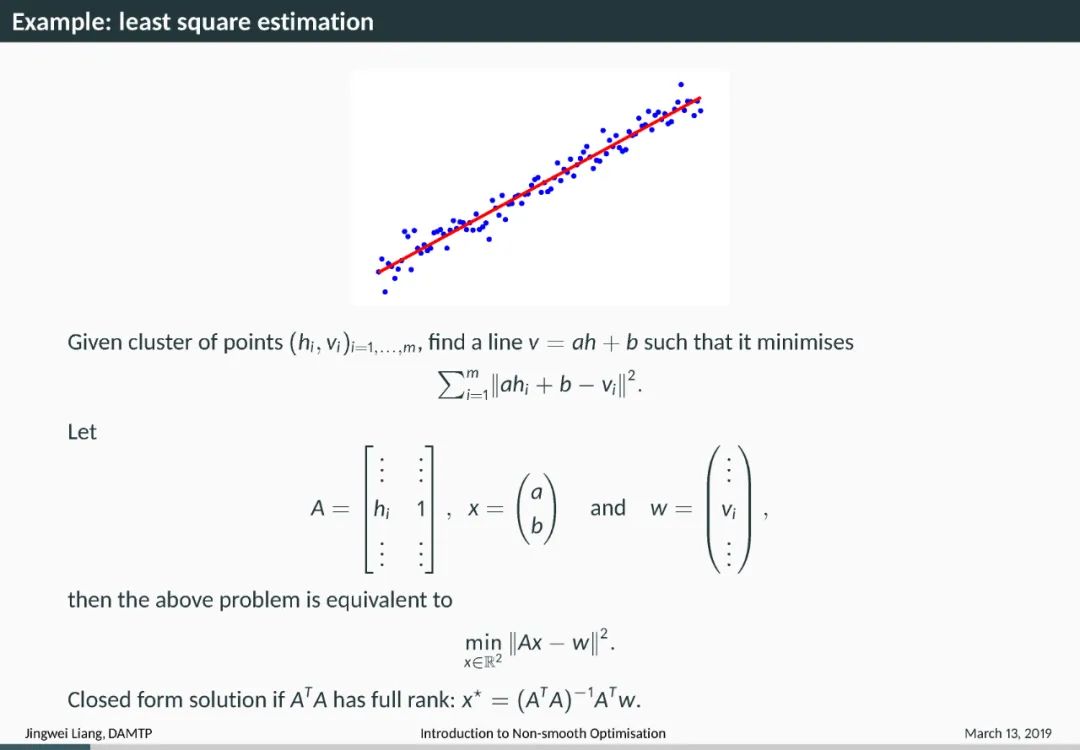
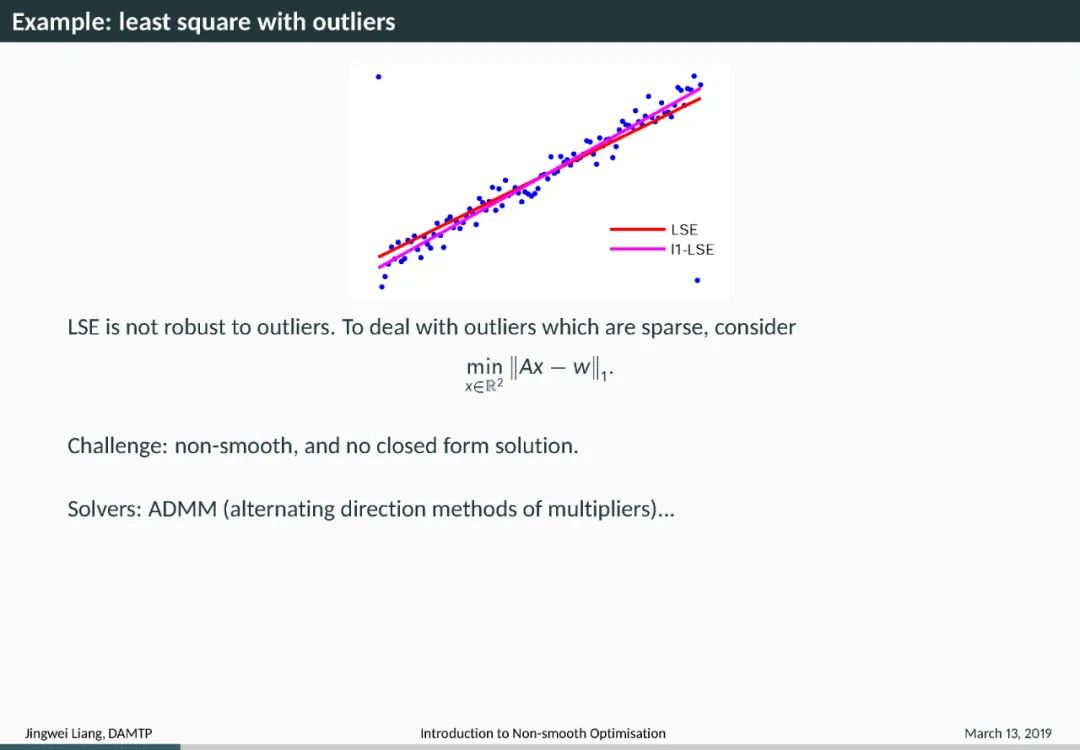
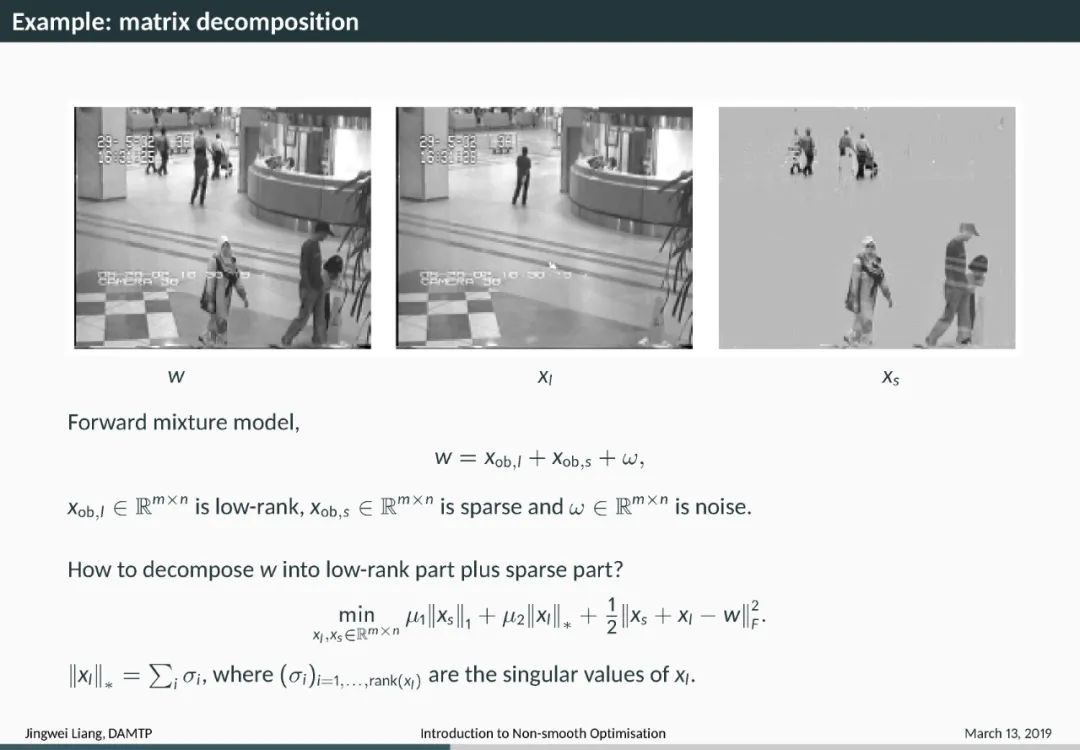
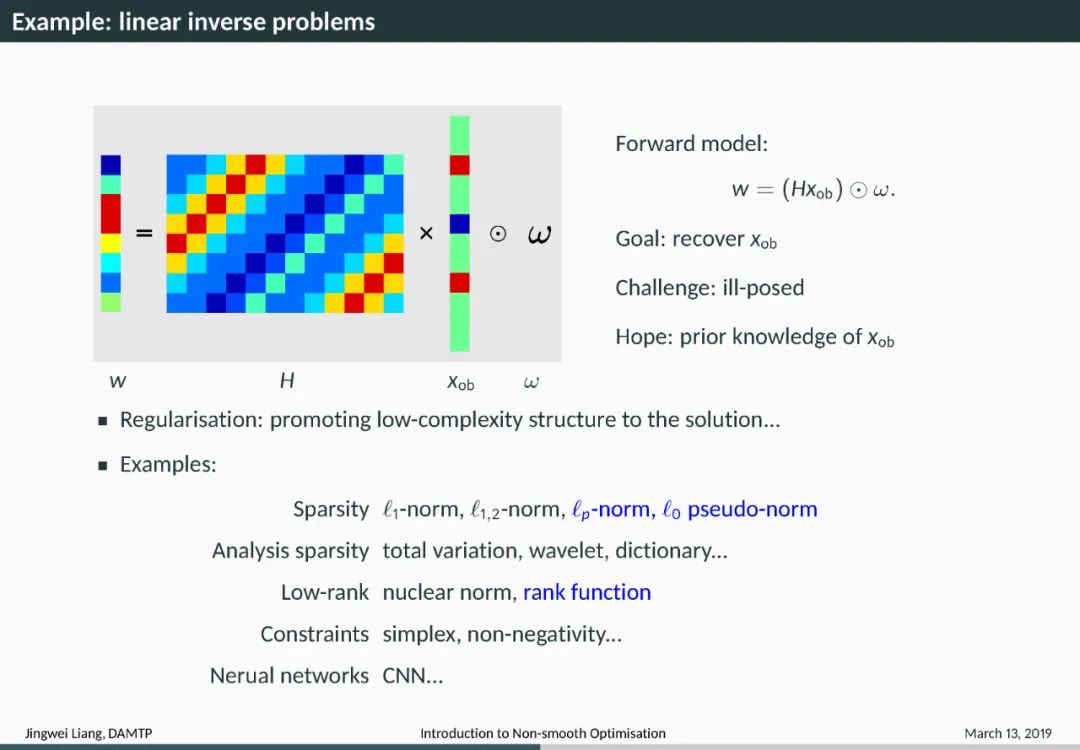
1. Introduction 导言

2. Gradient method 梯度方法

3. Proximal gradient method 近似梯度方法

4. Krasnosel'skii-Mann iteration 

5. Backward--Backward splitting

6. Douglas--Rachford splitting

7. Primal--Dual splitting

8. Other operator splitting methods

9. Alternating direction method of multipliers

10. Non-convex optimisation 非凸优化

11. Stochastic optimisation 随机优化

参考文献：

• S. Boyd and L. Vandenberghe. Convex optimization. Cambridge university press, 2004.

• R. T. Rockafellar. Convex analysis. Princeton university press, 2015.

• A. Beck. First-order methods in optimization. Vol. 25. SIAM, 2017.

• H. H. Bauschke and P. L. Combettes. Convex analysis and monotone operator theory in Hilbert spaces. Vol. 408. New York: Springer, 2011.

• B. Polyak. Introduction to optimization. Optimization Software, 1987.

• Y. Nesterov. Introductory lectures on convex optimization: A basic course. Vol. 87. Springer Science & Business Media, 2013.

专知便捷查看

便捷下载，请关注专知公众号（点击上方蓝色专知关注）

• 后台回复“NSO” 可以获取《最新《非光滑优化》十讲硬核课程，剑桥大学梁经纬博士主讲》专知下载链接索引

专 · 知

专知，专业可信的人工智能知识分发，让认知协作更快更好！欢迎注册登录专知www.zhuanzhi.ai，获取5000+AI主题干货知识资料！

欢迎微信扫一扫加入专知人工智能知识星球群，获取最新AI专业干货知识教程视频资料和与专家交流咨询！

点击“阅读原文”，了解使用专知，查看5000+AI主题知识资料