我们为什么要关心一个函数的凸凹性呢？

[遇见数学翻译小组] 核心成员: kitty

披着理科生外衣

努力探索双语教学

内心文艺感性的Cool Girl

英文: plus.maths.org/content/convexity, ★ 提示: 如果文中数字/公式显示较大, 请点击右上角中"刷新"即可恢复正常. 

函数是凸还是凹，这是一个我们通常仅仅通过观察就能来回答的问题。向外凸出是凸的，向内凸起是凹的。

▌国外凸函数是按照函数上方的区域是否为凸集定义, 国内有些教材中凸/凹函数定义刚好相反. 

但说到数学函数怎样判定，事情就没那么简单了。

麻省理工学院的一组计算机科学家最近发现，判断一个数学函数是否是凸函数是非常困难的。这个结果不仅让数学家感兴趣，也让工程师和任何从事优化工作的人感兴趣。而且幸运的是，该团队也找到了一种方法来解决这个问题，这种方法在现实生活中的大多数情况下都还适用。

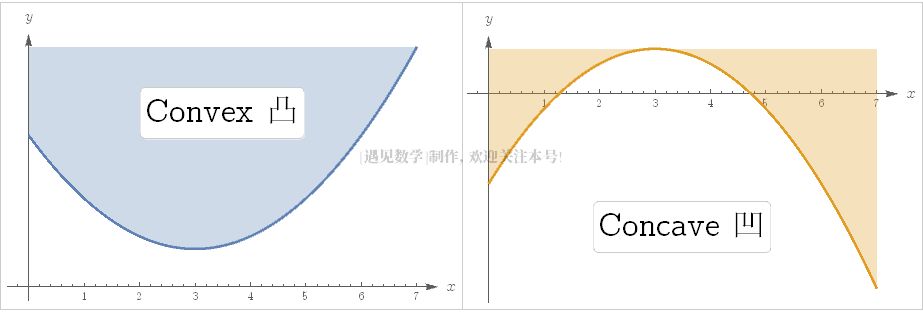
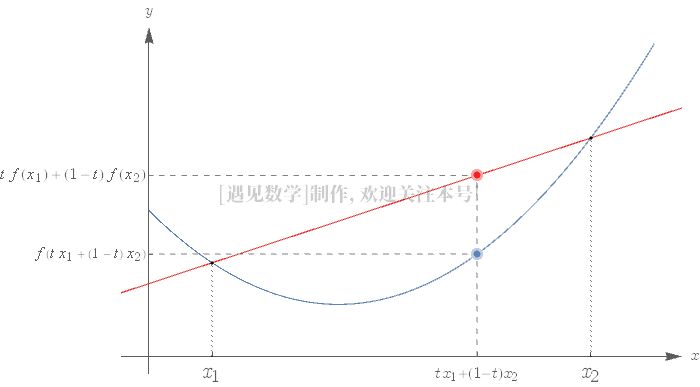
如果一个连续函数的图形上的面积是一个凸集，那么它就是凸的，换句话说，如果连接该图上任意两点的直线位于该图上两点之间的位之上。

更正式地说，一个函数   是凸的，如果对于任意的点   和   和所有在区间   范围内的 ，我们总是有

如果函数   是凸的，那函数   就是凹的。

(这些定义也适用于多个变量的函数，即函数 

要在讨论的点上有定义。在这种情况下 ，  应该被理解为由所涉及的变量组成的向量。)

 

(这些定义也适用于两个变量的凸函数图(上两图)和两个变量(下右图)的非凸函数图。

但是我们为什么要关心一个函数是否是凸的呢?

现实生活中的许多问题都涉及到最小化一些量。例如，如果你正在制造一辆汽车，你想要将燃油消耗降到最低，而这取决于汽车的重量和空气动力阻力等其他变量。如果给你一个数学函数用这些变量来描述燃料消耗，那么你的工作就是找到这个函数的全局最小值，也就是说，你需要找到一个点  ， 对所有在函数的定义域内的 ，都有   。

如果您正在研究一个更复杂的函数，可能是包含多变量的，那么要找到这个全局最小值绝非易事。

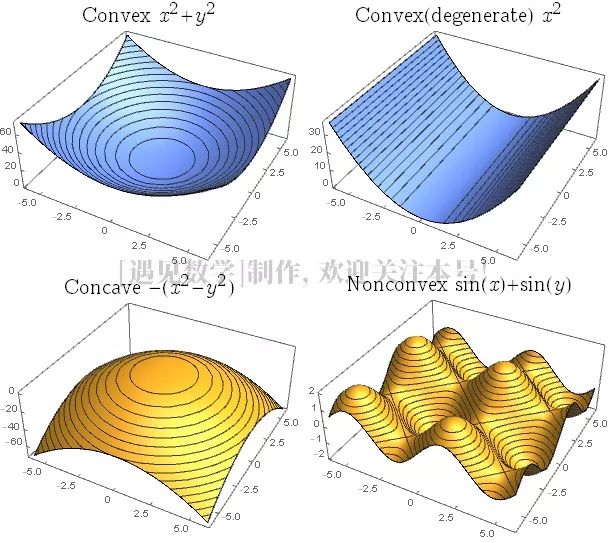
但是，如果函数是凸的，那么工作就简单得多了。凸函数只有一个极小值。从图像中可以看出，对于单一变量或双变量的凸函数，它们的形状像一个槽，最小值位于槽的底部。要找到这个值很容易，相当于使用“直觉”的技能在图像的斜率上寻找一下。(当你的函数有更多的变量时，这些方法也会起作用，这样你就不用绘制图形了。)

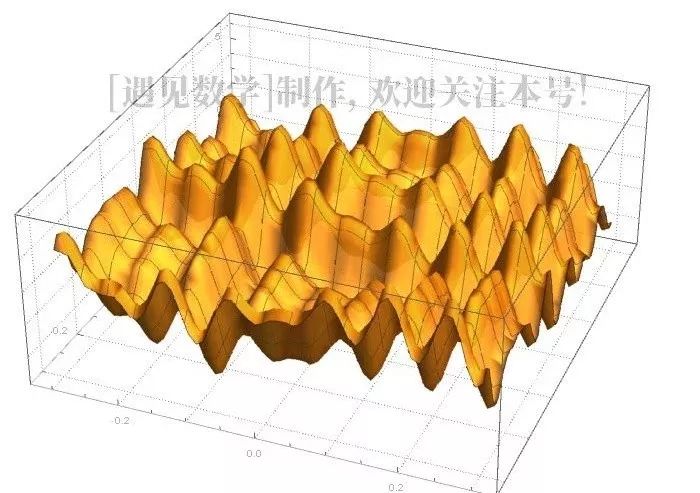
相比之下，一个非凸函数可以具有许多局部最小值，这让它的图像看起来像山脉一样。沿着山坡向下走，会让你进入其中一个山谷，但是你不能确定它仅仅是一个小的倾角还是你所追求的全局最小值。

▲ 一个非凸函数的图像

由于上述和其他一些原因，已知给定函数是否是凸函数是非常有用的。计算机能多快地检验给定函数是否是凸函数的问题，被认为是优化领域中最重要的七个问题之一。

这是Amir Ali Ahmadi，Alex Olshevsky，Pablo A. Parrilo和John N. Tsitsiklis在他们的论文中提出的问题。
(mit.edu/~a_a_a/Public/Publications/convexity_nphard.pdf)

该团队只研究了一类相对容易处理的函数，即多项式。这些函数是若干项的和，其中每一项都是变量的乘积，每一项都取幂，然后乘以常数，例如:

 

每一项的次数是各变量幂的和，整个多项式的次数是每一项的次数的最大值。在他们的论文中，研究人员只研究偶数次多项式，因为在奇数次情况下检查凸性很容易。

检验一个给定的多项式是否是凸的的方法是众所周知的，所以问题不在于此，而在于检验任意一个多项式需要多长时间。很明显，多项式中的项越多，问题就越难，所以我们希望答案取决于项的个数，而项的个数又与变量的个数有关。

在复杂的理论中，解决问题所需的“时间”是根据计算机完成任务所需的步骤数来衡量的。这取决于问题由多少个部分展开。例如，要找到一列数字中的最大项，您需要查看每个单独的数字，并将其与您迄今为止找到的最大数字进行比较。在算法中有  步，所以我们说它的执行时间是与   成正比的。其他问题可能与执行时间   ,   或   成正比( 是正数)。

这当然意味着执行时间的增长随着   的增长而增长相当快，初始问题的规模会变大。但与以   的指数倍增长的执行时间相比，这根本算不了什么。例如，一个正比于  的问题。

执行时间与某个多项式中的   成正比的算法称为多项式时间算法。它们被认为是相对较快的。这种算法可以解决的一类称为P问题。

▲  知道函数是否为凸函数可以帮助解决最小化问题，比如最小化汽车的燃料使用量。

但还有一类问题用 NP 表示(代表不确定时间多项式)。它的性质是如果有人给你这个问题的答案，你可以检查多项式时间是否正确。但是你能在多项式时间内从头开始解决这些问题吗?没有人确切知道。这是著名的 P=NP 问题的主题，这是数学中最大的开放问题之一。尽管还没有人能证明，一般的直觉是你不能: NP 问题的解可以被验证，但不能在多项式时间内找到。换句话说，P 不等于 NP。

现在我们回到凸性的问题。问题是一个算法的执行时间如何随着多项式中项数的增加而增长，该算法检查任意多项式的凸性。研究人员在他们的论文中表明，这个问题是 NP-困难的。这意味着，粗略地说，它至少和 NP 类中的任何问题一样难。所以除非有人证明了 P=NP，否则我们可以假设"它是凸的吗"这个问题不能用一种有效的时间方法来回答一个任意多项式。随着多项式中变量数量的增加，回答这个问题所需的时间也会激增。

但幸运的是，有一个漏洞。还有另一个性质，称为平方和凸性(sum of squared convexity)，它可以在多项式时间内检验。任何平方和为凸的多项式也是凸的。对于你在现实生活中可能遇到的大部分多项式来说，反过来也成立的: 如果它们是凸的，它们也是平方和也为凸函数。所以在这些例子中，检验平方和凸性就足够了。这给了我们乐观的理由: 也许凸性问题的困难在于一些非常棘手的多项式例子，但通常它们不会出现在实际应用中。(- End -)