脉络 - 自然、数学和美学环环相扣的一面

本文系台湾中央大学师资培育中心与数学系合聘单维彰教授的《文化脉络中的数学》课程里资工系学生林岳霖作业报告. 
原文: shann.idv.tw/Teach/liberal/kernel
[遇见数学] 略有修改, 转载请注明. 

诗歌与数学

学期开始，介绍 Escher 这位艺术家。谈到作品中有三大特色：「其一是『Image Impossible，代表作品《Waterfall》。后来无聊在网路上找到这个《Waterfall》，影片是『正确但是不可能』，很有趣喔。其二是『特殊的变型或周期性』。其三是『渐变(Morphing)』。因此有介绍到一系列的画作，其中有类似这样的图。

点击边框调出视频工具条

下边这张也是 Escher 的作品，起初以为只是具有著 Escher 特色二和特色三的普通画作而已。

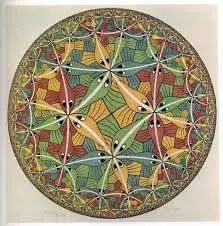
但是在期中考的前一周，处於极度涣散的某人，刚好看了 Margaret Wertheim 的演讲─《The beautiful math of coral》，才发现这张图片的不简单。

演讲的主题是：「数学家发明的钩针技术重建珊瑚礁生物，以颂扬珊瑚礁的神奇，并深入探讨以双曲几何为基础的珊瑚创作。」内容基本上都是从比较平易近人的角度切入。从雪花、碎形、叶片上的图案－这些美景存在于自然和物理，美学和数学的交叉路口。Margaret Wertheim 成立的塑形研究所，推动科学概念的审美观，从雪花和碎形这些自然物体，到人类建构物，如伊斯兰马赛克、绳索图形和编织。

而塑形研究所的最新计划可能是难以理解的奇怪－完全由钩针编织建造出珊瑚礁。这个计画利用了由珊瑚礁生物完美形塑的数学现象模型，以及如钩针编织这样的重复任务间美好的一致性－但得到的结果却也完全符合双曲空间模型。我们很容易沉迷於这个万花筒般，毛线形塑的珊瑚礁之美，但这个珊瑚礁计画有双重目的：「引起大众对世界各地珊瑚礁危机的注意，它们因为海洋盐水水面变化、过度捕捞、和无数的威胁而死亡；另外也展示出一个之前几乎不可能图示出的数学性质。借由形塑这些物理空间中的复杂方程式，这种技术可以帮助数学家看到图形模式和有所突破。」

里面的观点确实是很有趣。借由钩针编织，编织不同种类的数学定理。而珊瑚的钩针编织；这双曲空间的发现开创了数学领域，就是所谓的非欧几里德几何； 这实际上属于数学领域中广义相对论的基础。事实上，它向我们显示关于宇宙的形状。因此，这就是钩针编织─女性工艺品衔接於，欧几里德和广义相对论间的直接关联。

而双曲空间─非欧几里德几何和广义相对论又和 Escher 有什么关联呢？

Escher 的上幅图〈上图〉其实呈现得是双曲空间。每条鱼的大小事实上是一样的，同时圆周边界是在距圆盘中心无穷远的地方。上图是真实双曲空间的投影，为了将无穷大的空间放进有限的圆圈中内， 把远处的鱼压缩了。而如果不这样压缩，这个双曲空间将弯曲的很厉害。其中每一个小区域〈如下图〉会略像有皱折的马鞍形状。

非欧几里德几何和欧几里德几何和我们这堂文明脉络的数学可都是息息相关的。在第六讲的时候有详细介绍到欧几里德这个人、及他的著作。在第三讲「手绢中的宇宙」，有稍微介绍拓扑(topology)、莫比乌斯带(Möbius strip)、克莱因瓶(Klein bottle)。

而有了以上几点得相关知识，又令人不得不联想到─流形(Manifold)，是局   部具有欧几里德空间性质的空间。流形可以视为近看起来象欧几里德空间或其他相对简单的空间的物体。例如，人们曾经以为地球是平坦的，因为我们相对于地球很小，这是一个可以理解的假象。所以，一个理想的数学上的球足够小的区域也像一个平面，这使它成为一个流形。但是球和平面有很不相同的整体结构：如果你在球面上沿一个固定方向走，你最终回到起点，而在一个平面上，你可以一直走下去。流形可以是一个抽象空间。流形的技术使得我们能够独立考虑这些对象。从某种意义上来说，我们可以有一个不依赖於任何其他空间的球。

有很多不同种类的流形。最简单的是拓朴流形，它们局部看来像欧几里德空间。其他的变种包含了它们在使用中所需要的额外的结构。例如，一个微分流形不仅支持拓扑，而且要支持微积分。黎曼流形的思想导致了广义相对论的数学基础，使得人们能够用曲率来描述时空。

然而我们考虑一个拓扑流形，通常考虑三个例子: (1) 莫比乌斯带，它是有边界的流形。(2) 克莱因瓶，它在三维空间必须自交。以及(3)实射影平面，它很自然的出现在几何学中。

后记：这堂文明脉络的数学，让我学习到关于数学脉络的知识，明白自然和物理、数学和美学环环相扣的一面，以及彼此深深相依的那种感动。所以报告内容可能较为繁杂，但是希望借由这篇报告将我这学期，学习的脉络清楚展现。是一份报告，也是对自己一个交代。

参考资料：OOPS、Margaret Wertheim 的英语网上资料、科学人、维基

「予人玫瑰, 手留余香」感谢支持遇见!