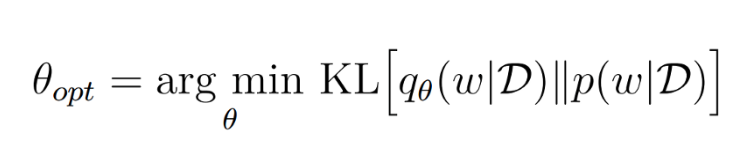贝叶斯神经网络(系列)：第二篇

本文为 AI 研习社编译的技术博客，原标题 ：

Bayesian Neural Network Series Post 2: Background Knowledge

作者 | Kumar Shridhar

翻译 | 微白o         

校对 | 酱番梨        审核 | 约翰逊·李加薪       整理 | 立鱼王

原文链接：

https://medium.com/neuralspace/bayesian-neural-network-series-post-2-background-knowledge-fdec6ac62d43

注：本文的相关链接请访问文末二维码

这是贝叶斯卷积网络系列八篇中的第二篇文章。

如需查看第一篇文章，请点击：贝叶斯神经网络(系列)第一篇

让我们将贝叶斯神经网络分解成贝叶斯和神经网络来开始。

贝叶斯推断是概率论和统计学机器学习中的重要组成部分。 它是基于由著名统计学家托马斯贝叶斯给出的贝叶斯定理。 在贝叶斯推断中，随着更多证据或信息的出现，假设概率得到更新。

另一方面，神经网络可以被认为是模仿人类大脑的端到端系统或一组算法（不是每个人都相信，但它是基础），并试图在数据集中学习复杂的表示来输出结果。

  神经网络

神经网络上已有非常好的教程。 我会试着简要介绍一下神经网络与大脑的类比，并着重解释我们以后要研究的概率论机器学习部分。

大脑的类比

感知器是由著名心理学家罗森布拉特（Rosenblatt）设想的描述神经元如何在我们的大脑中发挥作用的数学模型。 根据罗森布拉特的说法，神经元采用一组二进制输入（附近的神经元），将每个输入乘以连续值权重（每个附近神经元的突触强度），并且如果 sum足够大，则将这些加权输入的总和阈值输出为1，否则为0（同理神经元要么有效，要么无效）。

 生物激励神经网络（源地址：http://cs231n.github.io/neural-networks-1/）

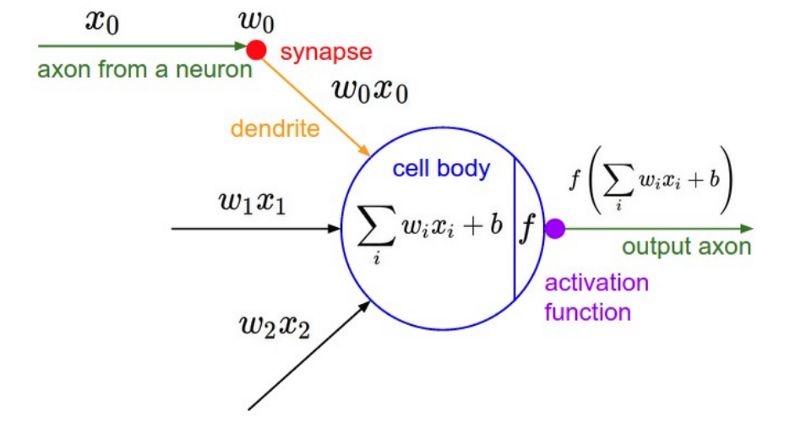
人工神经网络

受到生物神经系统的启发，人工神经网络（ANN）的结构被设计成像人脑一样处理信息。 大量深度互连的处理单元（神经元）协同工作使神经网络能够解决复杂的问题。 就像人类通过实例学习一样，神经网络也是如此。 在生物系统中学习涉及对突触连接的调整，其类似于神经网络中的权重更新。

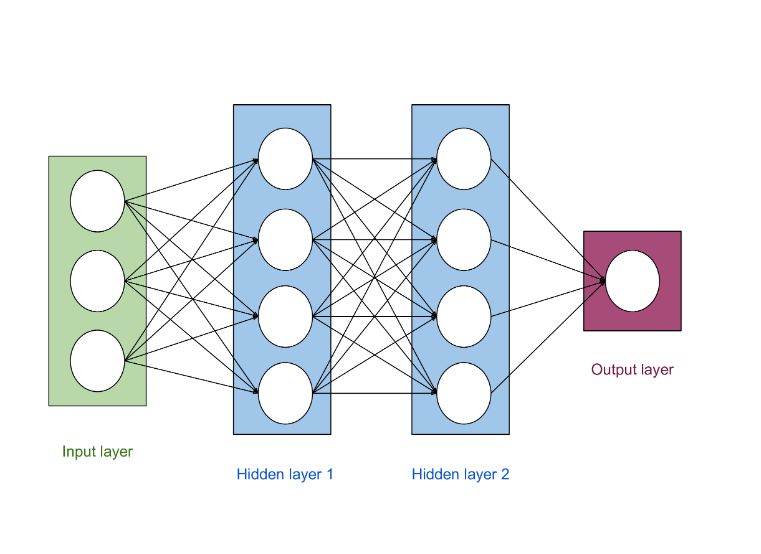
神经网络由三层组成：输入层为模型提供数据，隐藏层学习如何表示，输出层输出结果或预测。 神经网络可以被认为是一种端到端的系统，其可以在非常复杂的、不能由人教给机器的数据中找到一种特有的模式。

两个隐藏层的神经网络

卷积神经网络

休伯尔（Hubel）和威塞尔（Wiesel）在他们的层次模型中提到了一个神经网络，它在视觉皮层中有一个层次结构。 LGB（外侧膝状体）组成简单细胞，然后组成复杂细胞，继而形成低级超复合细胞，最终形成高级超复合细胞。

此外，低阶超复杂细胞和高阶超复杂细胞之间的网络在结构上类似于简单细胞和复杂细胞之间的网络。 在该层次结构中，较高级的细胞通常倾向于选择性地响应激励模式的更复杂的特征，低级细胞则倾向于简单特征。还有，较高阶段的细胞具有较大的感受野，并且对激励模式的位置变化不敏感。

与层次模型类似，神经网络起始层学习较简单的特征，如边缘，后续的神经层学习复杂的特征，如颜色，纹理等。此外，较高级的神经元具有较大的感受野，其构建在初始层上。然而，与多层感知器不同，其中来自同一层的所有神经元与下一层中的所有神经元连接，权重共享是卷积神经网络最主要的部分。示例：不像之前的做法，对于输入图像的每个像素（权重是28x 28），每个神经元都有不同的权重。现在神经元只有一个小的权重集（5 * 5），其应用于一大堆小的、相同大小的图像的子集中。第一层后的神经层都是以相似的方式工作，采用在之前隐藏层中找到的“局部”特征，而不是像素图像。并且连续地看到图像的较大部分，因为它们组合了关于图像的越来越多的子集信息。最后，最后一层对输出集进行了正确的预测。

如果数学上还不清楚的话，那么很显然上面的解释非常有用：如果没有这样的约束，神经网络将必须为图像的每个部分消耗大量时间学习完全相同的简单事物（例如检测边缘，角落等）。 但是由于存在约束，只有一个神经元需要学习每个简单的特征，并且总体上权重要少得多，它可以做得非常快！ 此外，由于这些特征的位置（精确到像素）无关紧要，神经元基本上可以跳过图像的相邻子集———即子采样，现在称为池化类型———当应用权重时，进一步减少了训练时间。 增加这两种类型的层——— 卷积层和池化层，是卷积神经网络（CNN / ConvNets）与普通旧的神经网络的主要区别。

   机器学习的概率论方法

为了简要叙述机器学习的概率论方法，我们把它分成概率论和机器学习分别讨论。

机器学习只是开发一些算法，在给定某些数据的情况下执行某些任务。 它包括从非结构化数据中查找模式来对电子邮件分类，从语言理解到自动驾驶汽车。 基于观察到的数据，通过机器学习方法进行一些推断。 训练模型从观察到的数据（训练数据）中学习一些模式和假设，并对未观察到的数据（测试数据）进行推断。由于每个推理都带有预测置信度，因此得出结论。 然而，由于多种原因，模型的预测可能不准确：输入噪声，噪声灵敏度，测量误差，非最佳超参数设置等。

机器学习中的概率模型表明，所有形式的不确定性都不是真正结果，而更像是概率，因此我们可以用概率论的知识来回答所有问题。 概率分布用于模拟学习，不确定性和未观察到的状态。 在观察数据之前定义先验概率分布，一旦观察到数据就开始学习，并且数据分布变为后验分布。 贝叶斯学习的基础就是用概率论的知识从数据中学习。

不确定性在贝叶斯学习中起着重要作用，来仔细研究不确定性的类型：

贝叶斯学习方法中的不确定性

（神经）网络中的不确定性是衡量模型预测的准确程度的指标。 在贝叶斯模型中，存在两种主要的不确定性类型：偶然不确定性和认知不确定性。

偶然不确定性衡量了观测中固有的噪声。 这种类型的不确定性存在于数据收集方法中，比如伴随数据集的均匀的传感器噪声或运动噪声。 即使收集更多数据，也不能减少不确定性。

认知不确定性是模型本身造成的不确定性。 给定更多数据可以减少这种不确定性，并且通常称为模型不确定性。偶然不确定性可以进一步分为同方差不确定性，不同输入下不变的不确定性，以及取决于模型输入的异方差不确定性，其中一些输入可能具有比其他输入更多的噪声输出。 异方差的不确定性尤为重要，它可以防止模型的输出过于优化。

可以通过在模型参数或模型输出上加入概率分布来估计不确定性。 通过在模型的权重上加入先验分布，然后尝试捕获这些权重在给定数据的情况下变化多少来对认知不确定性建模。 另一方面，偶然不确定性，是通过在模型的输出上加入分布来建模的。

现在，我们对概率机器学习基础，贝叶斯学习和神经网络有了一个很好的认识。 将贝叶斯方法和神经网络结合看起来是一个不错的想法，但在实践中，训练贝叶斯神经网络是很难的。 训练神经网络最流行的方法是反向传播，我们用它来训练贝叶斯神经网络。 我们来详细介绍一下这些方法。

   反向传播

鲁姆哈特在1986年提出了神经网络中的反向传播，它是训练神经网络最常用的方法。 反向传播是一种根据网络权重计算梯度下降的技术。 它分两个阶段运行：首先，输入特征通过网络的正向传播，以计算函数输出，从而计算与参数相关的损失。 其次，训练损失对权重的导数从输出层传回输入层。这些已计算的导数还用于更新网络的权重。 这是一个连续的过程，权重在每次迭代中不断更新。

尽管反向传播很受欢迎，但是在基于反向传播的随机优化中存在许多超参数，其需要特定的调整，例如学习率，动量，权重衰减等。找到最优值所需的时间与数据大小成比例。 对于使用反向传播训练的网络，仅在网络中实现权重的点估计。 结果，这些网络得出了过度的预测结果，并没有考虑参数的不确定性。 缺乏不确定性方法会使（神经）网络过拟合并需要正则化。

神经网络的贝叶斯方法提供了反向传播方法的缺点，贝叶斯方法自然地解释了参数估计中的不确定性，并且可以将这种不确定性加入到预测中。

此外，对参数值取均值而不是仅选择单点估计值使得模型对过拟合具有鲁棒性。

过去已经提出了几种用于贝叶斯神经网络学习的方法：拉普拉斯近似，MC丢失和变分推理。 我们使用反向传播的贝叶斯来完成的工作，接下来进行说明。

反向传播的贝叶斯

贝叶斯反向传播算法石油Blundell等人提出的，用于学习神经网络权重的概率分布。 整个方法可归纳如下：

该方法不是训练单个网络，而是训练网络集合，其中每个网络的权重来自共享的学习概率分布。 与其他集合方法不同，该方法通常仅使参数的数量加倍，然后使用无偏的蒙特卡罗梯度估计来训练无穷集合。

通常，对神经网络权重的精确贝叶斯推断是难以处理的，因为参数的数量非常大，并且神经网络的函数形式不适合精确积分。 相反，我们采用变分近似而不是蒙特卡罗方法来找到似然贝叶斯后验分布。

好了，至此我们已经说通了。 那再深入一点，因为这个方法构成了我们方法的基础，将在后面的博客中进行解释。 我们首先需要理解为什么分布变得难以处理以及需要近似它。 让我们从贝叶斯定理开始：

 贝叶斯定理

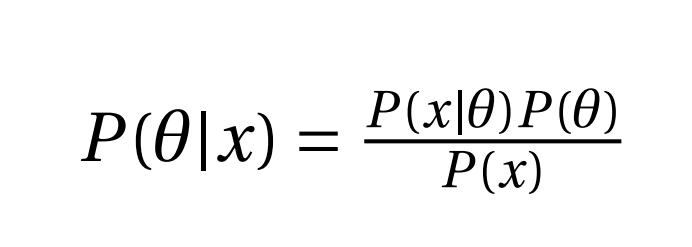
如上所述，根据贝叶斯定理，我们试图在给定一些数据x的情况下找到模型参数θ的概率。 这被称为后验，我们想计算它。 现在分子的P（θ）是我们的先验（在看到数据之前的估计）和P（x |θ）这是可能性并且显示数据分布。 这两个值都很容易计算。 分母P（x）是证据，它显示数据x是否是从模型生成的。 现在，事情有点棘手了， 我们只能通过整合所有可能的模型值来计算：

可见，这个积分使得整个过程难以处理，解决它的唯一方法是近似它。 因此，我们将使用变分推理来近似函数形式。

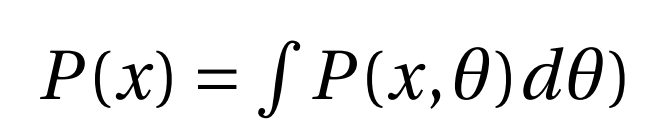
还有其他方法可用于近似积分，而流行的方法是马尔可夫链蒙特卡罗和蒙特卡洛丢弃法。

变分推论

假设我们有所有的密度函数，并且想估计它。 我们首先选择一个分布（可以是高斯分布，因为它最常用），一直修改到非常接近我们想要的函数，即后验概率。 我们希望尽可能接近真正的分布，其是难以直接处理的，我们可以通过最小化两者之间的相对熵来完成。

因此，我们有一个函数P(w|D)（上面得到的后验概率），我们想用另一个分布q(w|D)用一些变分参数θ来近似它。

注意到此处的符号已更改，以使其与费利克斯 · 劳曼伯格概率深度学习保持一致：反向传播的贝叶斯理论可以很好地解释它。

相对熵使问题成为优化问题，并可以最小化为：

一张图很好地展示如何近似难处理的后验概率

来源：https://medium.com/neuralspace/probabilistic-deep-learning-bayes-by-backprop-c4a3de0d9743

但这不是结束。 如果我们解决相对熵，由于存在积分函数，又出现了一个难以处理的方程：

 源地址：https://arxiv.org/abs/1806.05978

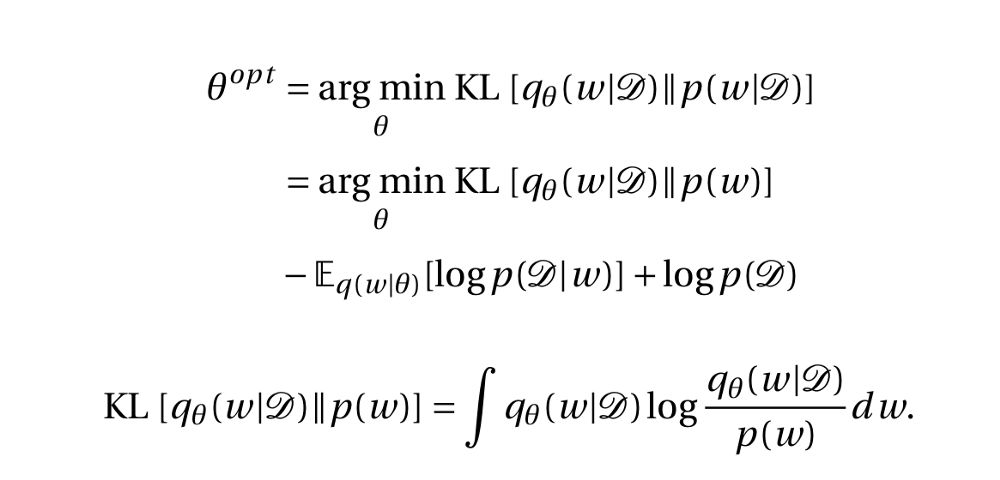
现在我们已经无法近似一个近似函数了。 因此，我们可以从近似函数q(w|D)中进行采样，因为从近似函数q(w|D)中采样权重要比难处理的真后验函数p（w | D）容易。 在这样做时，我们得到如下所述的易处理函数：

这些采样权重w，被用在神经网络的反向传播中去学习后验分布。

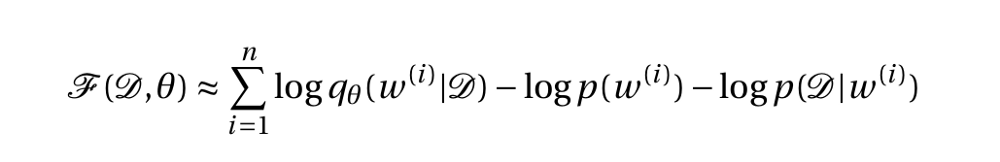
现在，正如我们所看到的，可以通过反向传播方法训练贝叶斯神经网络，并且贝叶斯神经网络能自动合并正则化。 我们将在接下来的博客中学习使用变分推理方法的贝叶斯卷积神经网络。 我们在卷积中使用两个操作（更多细节在即将发布的博客中或在此处阅读），因此与基于CNN的点估计相比，贝叶斯卷积神经网络的参数数量翻倍。 因此，为了减少网络参数，我们精简了神经网络架构，让我们看看它是如何完成的。

   反模型权重剪枝

模型剪枝减少了深度神经网络中各种连接矩阵的稀疏性，从而减少了模型中有价值的参数的数量。模型剪枝的整个想法是减少参数的数量而不会损失模型的准确性。 这减少了使用正则化的大型参数化模型的使用，并促进了密集连接的较小模型的使用。 最近的一些工作表明，网络可以实现模型尺寸的大幅减少，同时精度也相差无几。模型剪枝在降低计算成本，推理时间和能量效率方面具有几个优点。 得到的剪枝模型通常具有稀疏连接矩阵。 使用这些稀疏模型的有效推断需要有能加载稀疏矩阵并且/或者执行稀疏矩阵向量运算的专用硬件。 但是，使用新的剪枝模型可以减少总体内存使用量。

有几种方法可以实现剪枝模型，最常用的方法是将低贡献权重映射到零并减少整体非零值权重的数量。 这可以通过训练大型稀疏模型并进一步修剪来实现，这使其与训练小型密集模型相当。

通过应用L_0（L-zero）范数可以形式化为大多数特征赋予权重零和仅向重要特征分配非零权重，因为它对所有非零权重应用恒定惩罚。L_0范数可以被认为是特征选择器范数，其仅将非零值分配给重要的特征。 然而，L_0范数是非凸的，因此，不可微分使得它成为NP-hard问题并且只能在P = NP时有效地求解。L_0范数的替代是L_1范数，其等于绝对权重值的总和。 L_1范数是凸的，因此是可微分的，可以用作L_0范数的近似值。 L_1范数通过令大量系数等于零而充当稀疏促进正则化器，是一个很好的特征选择器。

这篇博客只是为了提供以后的博客中使用的术语和概念的背景知识，如果我遗漏了什么，请告诉我。

如果您想提前阅读，请查看论文工作或论文。

PyTorch中的实现点击阅读原文可获得。

如需查看第一篇文章，请点击：贝叶斯神经网络(系列)第一篇

想要继续查看该篇文章相关链接和参考文献？

点击底部【阅读原文】或长按下方地址/二维码访问：

https://ai.yanxishe.com/page/TextTranslation/1466

AI求职百题斩 · 每日一题

每天进步一点点，扫码参与每日一题！

点击 阅读原文 查看本文更多内容↙