【机器学习】三层神经网络

本文介绍了传统的三层神经网络模型，首先介绍了网络中的神经单元概念，将一个神经单元视为一个逻辑回归模型。因此，神经网络可以看作是逻辑回归在（宽度，深度）上的延伸；然后，前向传播是一个复合函数不断传播的过程，最终视目标而定损失函数；最后，反向传播则是对复合函数求导的过程。当然三层神经网络只是深度学习的雏形，如今深度学习已经包罗万象。

作者 | 文杰

编辑 | yuquanle

三层神经网络

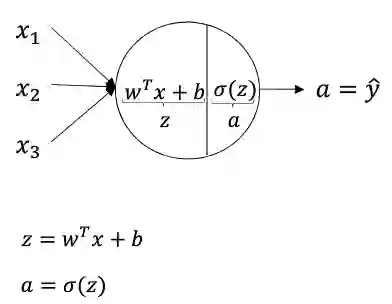
A、神经单元

深度学习的发展一般分为三个阶段，感知机-->三层神经网络-->深度学习（表示学习）。早先的感知机由于采用线性模型，无法解决异或问题，表示能力受到限制。为此三层神经网络放弃了感知机良好的解释性，而引入非线性激活函数来增加模型的表示能力。三层神经网络与感知机的两点不同：

1）非线性激活函数的引入，使得模型能解决非线性问题。

2）引入激活函数之后，不再会有 损失的情况，损失函数采用对数损失，这也使得三层神经网络更像是三层多元（神经单元）逻辑回归的复合。

神经网络中每一个神经元都可以看作是一个逻辑回归模型，三层神经网络就是三层逻辑回归模型的复合，只是不像逻辑回归中只有一个神经元，一般输入层和隐藏层都是具有多个神经元，而输出层对应一个logistic回归单元或者softmax单元，或者一个线性回归模型。

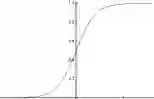
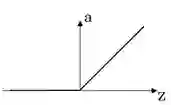
这里对一些常用的非线性激活函数做一些简单的介绍（图像，性质，导数）：

性质：对于以上几个非线性激活函数都可以看作是

的一个近似。采用近似的一个重要原因是为了求导，早起常采用平滑的sigmoid和tanh函数，然而我们可以发现这两个函数在两端都存在导数极小的情况，这使得多层神经网络在训练时梯度消失，难以训练。而Relu函数则很好的解决两端导数极小的问题，也是解决神经网络梯度消失问题的一种方法。

导数：

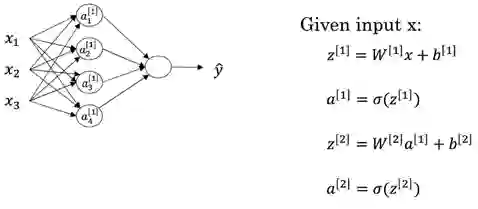
B、前向传播

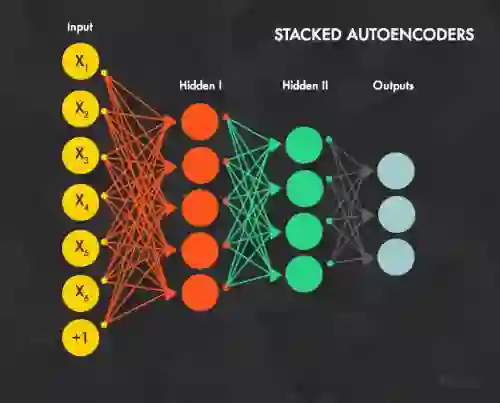
前向传播是一个复合函数的过程，每一个神经元都是一个线性函数加一个非线性函数的复合，整个网络的结构如下：其中上标表示网络层，所以 表示输出层。

向量形式：

矩阵形式：

其中线性函数还是 ，不过要注意的是这里由于每一层不仅一个神经元，所以逻辑回归中的向量 则扩展为矩阵，表示有多个神经元（也正是因为多个神经元，导致神经网络具有提取特征的能力）。非线性函数则可以有以下选择，目前来看Relu函数具有一定的优势。

其中值得注意的是矩阵的行列，深度学习常采用一列表示一个样本，所以网络中数据矩阵的大小如下：

损失函数同样采用对数损失(二分类)：

C、反向传播

由于神经网络是一个多层的复合函数，前向传播就是在计算复合函数，所以反向传播就是一个链式求导过程，确定所有参数的负梯度方向，采用梯度下降的方法来更行每一层网络的参数。

1.损失函数：

2.激活函数：

3.线性函数：

对于损失函数直接对各个变量求导如下：

值得注意的是激活函数是一个数值操作，不涉及矩阵求导，线性函数中 是因为 是作用于 个样本，所以在确定负梯度方向时需要 个样本取均值，而对 求导则不需要求均值。

代码实战

int trainDNN()
{
    Matrix x;
    char file[20]="data\\train.txt";
    x.LoadData(file);
    x = x.transposeMatrix();
    cout<<"x,y"<<endl;
    cout<<"----------------------"<<endl;
    Matrix y;
    cout<<x.row<<endl;
    y=x.getOneRow(x.row-1);
    x.deleteOneRow(x.row-1);
    y=one_hot(y,2);
    cout<<x.row<<"*"<<x.col<<endl;
    cout<<y.row<<"*"<<y.col<<endl;
    const char *initialization="he";
    double learn_rateing=0.1;
    int iter=1000;
    double lambd=0.1;
    double keep_prob=0.5;
    bool print_cost=true;
    const char *optimizer="gd";
    int mini_batch_size=64;
    double beta1=0.9;
    double beta2=0.999;
    double epsilon=0.00000001;

    DNN(x,y,optimizer="gd",learn_rateing=0.001,initialization="he",lambd=0.001,keep_prob = 1,mini_batch_size=64, \
        beta1=0.9, beta2=0.999, epsilon=0.00000001, iter=5000, print_cost=true);
    predict(x,y);
    return 0;
}

int DNN(Matrix X,Matrix Y,const char *optimizer,double learn_rateing,const char *initialization, double lambd, double keep_prob, \
        int mini_batch_size,double beta1, double beta2, double epsilon, int iter, bool print_cost)
{
    /**
    初始化参数
    **/
    int i=0,k=0;
    int lay_dim=3;
    int lay_n[3]= {0,3,1};
    lay_n[0]=X.row;
    string lay_active[3]= {"relu","relu","sigmoid"};
    sup_par.layer_dims=lay_dim;
    for(i=0; i<lay_dim; i++)
    {
        sup_par.layer_n[i]=lay_n[i];
        sup_par.layer_active[i]=lay_active[i];
    }
    init_parameters(X,initialization);
    double loss;

    Matrix AL(Y.row,Y.col,0,"ss");
    double *keep_probs;
    if(keep_prob==1)
    {
        keep_probs=new double (sup_par.layer_dims);
        for(k=0;k<sup_par.layer_dims;k++)
        {
            keep_probs[k]=1;
        }
    }
    else if (keep_prob<1)
    {
        keep_probs=new double (sup_par.layer_dims);
        for(k=0;k<sup_par.layer_dims;k++)
        {
            if(k==0 || k==sup_par.layer_dims-1)
            {
                keep_probs[k]=1;
            }
            else
            {
                keep_probs[k]=1;
            }
        }
    }
    for(i=0; i<iter; i++)
    {
        //cout<<"-----------forward------------"<<"i="<<i<<endl;
        AL=model_forward(X,keep_probs);
        //cout<<"-----------loss--------------"<<endl;
        loss=cost_cumpter(AL,Y,lambd);
        if(i%100==0)
            cout<<"loss="<<loss<<endl;
        //cout<<"-----------backword-----------"<<endl;
        model_backword(AL,Y,lambd,keep_probs);

        //cout<<"-----------update--------------"<<endl;
        updata_parameters(learn_rateing,i+1,optimizer,beta1,beta2,epsilon);
    }
    predict(X,Y);
    return 0;
}

int predict(Matrix X,Matrix Y)
{
    int i,k;
    parameters *p;
    p=∥
    p->A = X.copyMatrix();
    Matrix AL;
    double *keep_probs=new double [sup_par.layer_dims];
    for(k=0;k<sup_par.layer_dims;k++)
    {
        keep_probs[k]=1;
    }
    AL=model_forward(X,keep_probs);
    for(i=0;i<Y.col;i++)
    {
        if(AL.data[0][i]>0.5)
            AL.data[0][i]=1;
        else
            AL.data[0][i]=0;
    }
    double pre=0;
    for(i=0;i<Y.col;i++)
    {
        if((AL.data[0][i]==1 && Y.data[0][i]==1)||(AL.data[0][i]==0 && Y.data[0][i]==0))
            pre+=1;
    }
    pre/=Y.col;
    cout<<"pre="<<pre<<endl;
    return 0;
}

---

本文转载自公众号：AI小白入门，作者：文杰

推荐阅读

SemBERT: BERT 的语义知识增强

BERT fintune 的艺术

子词技巧：The Tricks of Subword

T5 模型：NLP Text-to-Text 预训练模型超大规模探索

BERT 瘦身之路：Distillation，Quantization，Pruning

Transformer (变形金刚，大雾) 三部曲：RNN 的继承者

关于AINLP

AINLP 是一个有趣有AI的自然语言处理社区，专注于 AI、NLP、机器学习、深度学习、推荐算法等相关技术的分享，主题包括文本摘要、智能问答、聊天机器人、机器翻译、自动生成、知识图谱、预训练模型、推荐系统、计算广告、招聘信息、求职经验分享等，欢迎关注！加技术交流群请添加AINLP君微信(id：AINLP2)，备注工作/研究方向+加群目的。