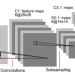
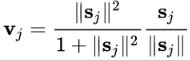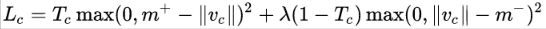如何看待 Hinton 那篇备受关注的Capsules论文？

本文原作者 SIY.Z，本文整理自作者在知乎《如何看待 Hinton 的论文 Dynamic Routing Between Capsules？》问题下的回答。AI 研习社已获得转载授权。

Capsule 是 Hinton 近几年在采访中频繁提到的概念，在之前我写过一个详尽的概述：  浅析 Hinton 最近提出的 Capsule 计划   ，由于 Capsule 的基础概念相关的知识非常多，这里全部列出来恐怕不合适，如果想详细了解 Capsule 的理念，我建议先参考这个概述。论文中很多抽象的论述都和 Hinton 之前的这些想法密切相关。

论文原文及全文翻译见：  全文翻译 Hinton 那篇备受关注的 Capsule 论文  

关注 AI 研习社，回复【论文】即可获取论文原文及翻译。

  应该关注的地方

理念归理念，论文归论文，应用归应用。对于这篇公开的论文，我认为我们应该关注这些地方：

1. 这篇论文的定位是什么？

答：
我想论文中说的非常清楚：The aim of this paper is not to explore this whole space but to simply showthat one fairly straightforward implementation works well and that dynamic routing helps.
也就是这篇论文仅仅是为了实现一个简陋的，能用的基于 capsule 的模型，原则上无论结果多么差都可以接受。而结果还是基本令人满意的，并且动态路由算法似乎能提升算法性能。作者并没有精心设计高效可扩展的算法，而是仅仅展示 capsule 是能用的。
Hinton 提 Capsule 已经提了相当一段时间了，但是基本没有具体的算法和模型实现。一个还称得上实现的是 2011 年的论文 [1]，但是显然那个实现和 Hinton 的想法相差很远。
所以，这次 paper 是 Hinton 他们的初步实现，改进空间很大，没有必要大规模炒作（这样被误导看了论文反而觉得印象很差）。很多 Hinton 在演讲中提到的成果（包括 few-shot learning 等等）论文里面还没有看到，也就意味着 Hinton 可能还有一些更加成熟的关于 capsule 的论文没有发表。

2. 就理念而言，这篇论文践行了 Hinton 的哪些理念，而哪些论文还没有达到？而践行这些理念使用哪些具体的数学方法？
答：这篇论文基本践行了 Hinton 对的 Capsule 的观念，但是某些地方没有体现：
（1）coincidence filtering(参考 [2])。这是 Hinton 理念上的 “routing” 方案，看上去非常 robust，但是实施需要 EM 算法和 Gaussian Mixture，相对比较复杂。而这次论文中我们可以看到它直接用非常简单粗暴的 dynamic routing 来实现了（并且引入新的超参数），这有点偏离原来的思想。
（2）place-coding & rate-coding (参考 [2])。这需要多层 capsule 才能体现，论文中的模型实在太浅了完全不能体现。

3. 就论文而言，论文有什么亮点，有什么突破？将来有什么展望？
答：亮点和突破在于更好的 robust，以及对重叠图像 / 多物体识别的先天优势。这个正文会细说。

4. 就应用而言，这篇论文中的 Capsules 是否有传统的深度学习不可替代的价值？又有什么应用场景？
答：对不起，目前看来还不明显。不过这也不是论文的目标。

  用一组 Capsules 替代网络的一层

Capsule 关键的一点是在于用复杂的 Capsule 替代现在神经网络中简单的 layer。

其重要理由之一是现在 layer 中的 neuron 太过简单，本身很难表征概念；而 Capsule 使用向量作为输入输出，而向量就可以作为良好的表征（比如 word2vec 中的向量就可以良好表征词汇），可以加各种特技，（具体原因，包括生理学，心理学上的原因参见 [2]）。

与一般的向量表征不同，Capsule 的输出向量表征了两个部分：

1. 其长度表征了某个实例（物体，视觉概念或者它们的一部分）出现的概率

2. 其方向（长度无关部分）表征了物体的某些图形属性（位置，颜色，方向，形状等等）

用 Capsules 代替 layer 存在几个问题：

(1) 如何实现激活函数？layer 使用了非线性函数来处理标量，而 Capsule 处理的是向量，那么又该用什么 “激活函数” 呢？
答案是一个被称为 “squashing” 的非线性函数，（s 为输入，v 为输出，j 为 capsule 的序号）

即

，其中  是单位化向量，也就是缩放向量的长度为 。

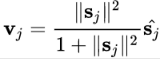
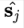
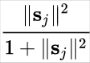
它画出来如下：

长度缩放函数

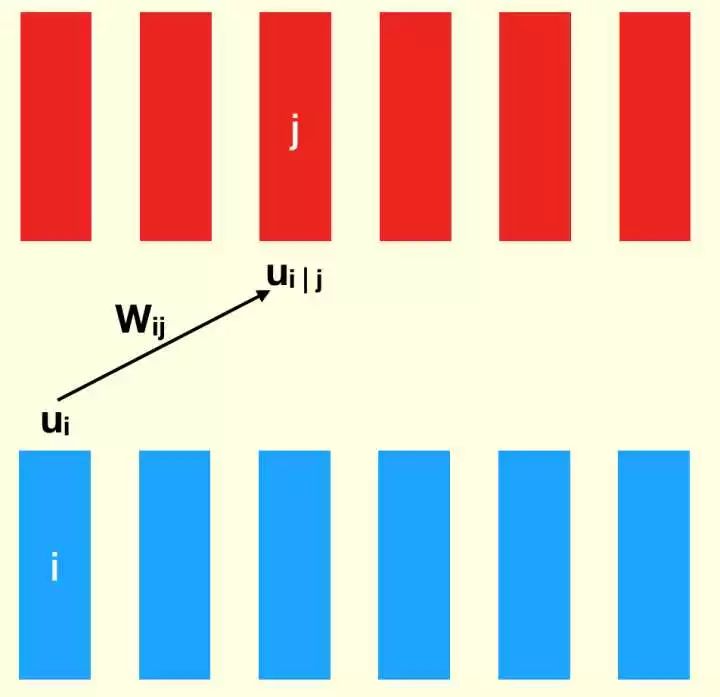
这个函数的特点是：

1. 值域在 [0,1] 之间，所以输出向量的长度可以表征某种概率。

2. 函数单调增，所以 “鼓励” 原来较长的向量，而 “压缩” 原来较小的向量。

也就是 Capsule 的 “激活函数” 实际上是对向量长度的一种压缩和重新分布。

(2) 如何处理输入？layer 使用了矩阵，本质上是上层输出的线性组合。那么对于 Capsule 又应该怎么做呢？

Capsule 处理输入分为两个阶段：线性组合和 routing。

线性组合一定程度上是借用 layer 中的线性组合的概念，用在 Capsule 中的好处和作用来自于图形学对 Hinton 的启示（参见 [2]）。

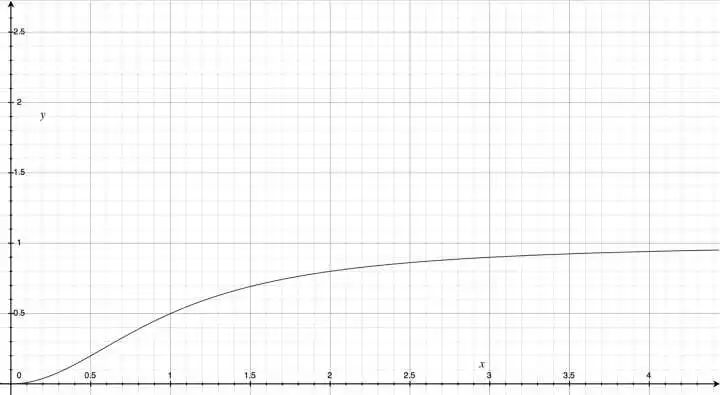
不过这个线性组合不是针对 layer（也就是只有一个 matrix），而是针对 capsules （一堆 matrices），亦即:

（其中 u 是下层的向量，由前层的标号为 i 的 capsule 产生，带帽子的 u 是处理后的结果，送给后层的标号为 j 的 capsule）。

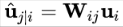
这等于，原来 NN 中的 “边权”（常量）变成了矩阵。

线性组合部分示意图

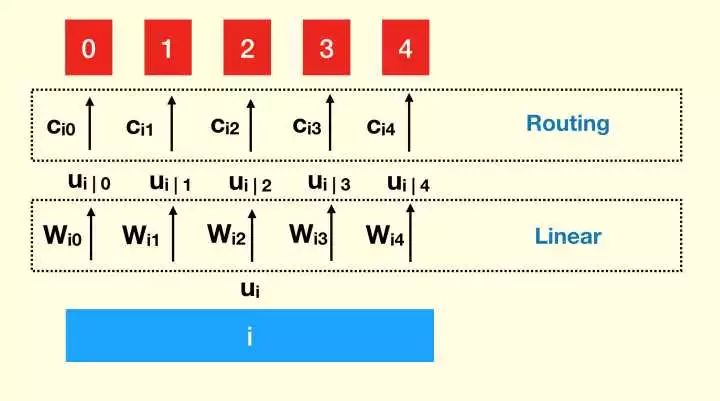
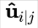
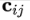
关于 routing 部分，其实是给 加权求和，权重是。

routing 和 线性组合相结合

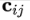
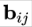
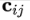
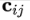
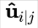
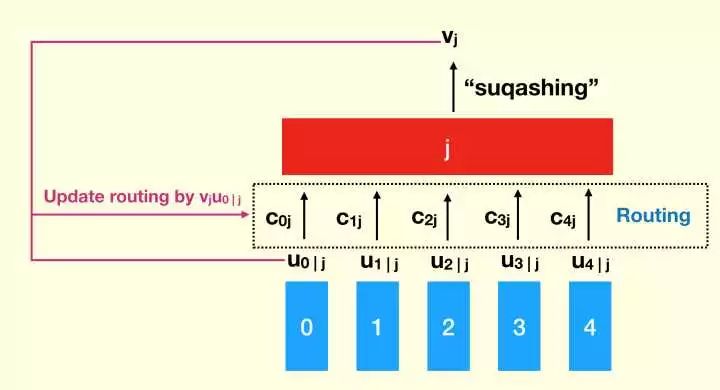
而 是 softmax 的结果，从而使得 分布归一化；并且由于 softmax 会使分布 “尖锐化”，从而只有少数 有较大的取值，这样就起到了 routing 的作用（只有少数 的权重较大，就好像底层的某个 capsule 的输出只贡献给上面的某个 capsule）。

  Routing 的更新：Updating by agreement

按照 Hinton 在很多视频中的理念，“找到最好的（处理）路径等价于（正确）处理了图像”。这也是 Capsule 框架中引入 Routing 的原因之一。

而找到 “最好路径” 的方法之一就是找到最符合输出的输入向量。符合度通过输出向量和输入向量（线性变换后的向量）的内积所表征，这个符合度直接被加入到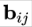 中 。

更新算法示意图

更新算法

这个更新算法很容易收敛。论文中认为 3 次足矣。routing 和其他算法一样也有过拟合的问题，虽然增加 routing 的迭代次数可以提高准确率，但是会增加泛化误差，所以不宜过多迭代。

  网络结构：CapsNet

网络结构在论文中称为 CapsNet。

首先，来一个标准的 CNN+ReLU。强迫症患者可能感到不是很舒服：为什么不全部使用 Capsule，而是要来个 CNN 呢？

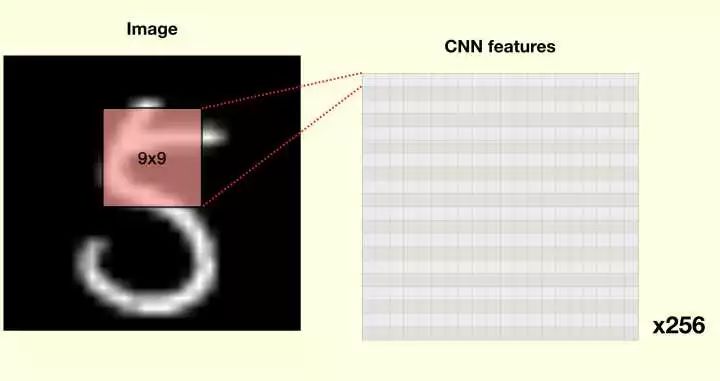
第一层，标准的卷积

原因其实很简单，Capsule 的向量是用来表征某个物体的 “实例”，并且按照假设，越高级的 capsule 能够表征更高级的实例。如果不通过 CNN 抽取特征，那么 Capsule 就直接得到图片的内容，这并不是很理想的低级特征。而浅层的 CNN 却擅长抽取低级特征，于是用 CNN 是在情理之中的。

这里注意到 CNN 的感知野很大（9*9，现在一般 3*3），这是因为 CNN 层数很少的情况下，感知野越大，底层的 capsules 能够感知到的内容也越多。

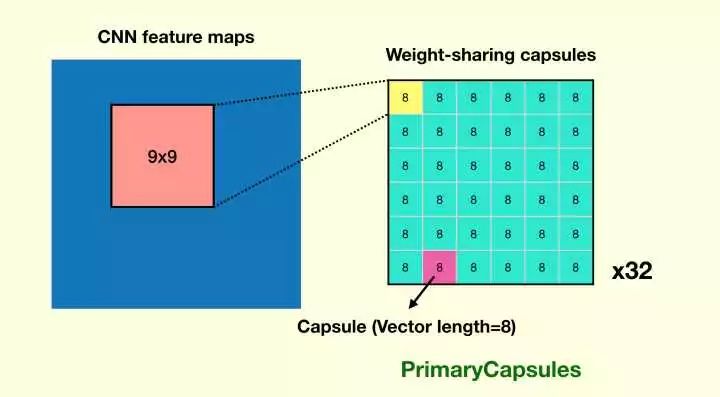
但是，一层 CNN 的能力不足以抽取到合适的特征，于是这篇论文又加了一个 CNN 层（一共 32 个 CNN，文中称为 32 个 channels，每个 CNN 有 8 个 filters），这个 CNN 的输出构成了第一层 Capsules 的向量。

由于 CNN 共享权值的特点，这一层每个 CNN 输出的 feature map 中的 36 个 capsules 是共享权值的（通过 CNN）。显然所有的 Capsules 都共享权值是有问题的，这也是为什么这层搞 32 个 CNN 的道理：不同的 CNN 输出的 Capsules 间是独立的。

第二层，通过卷积生成初级 Capsules

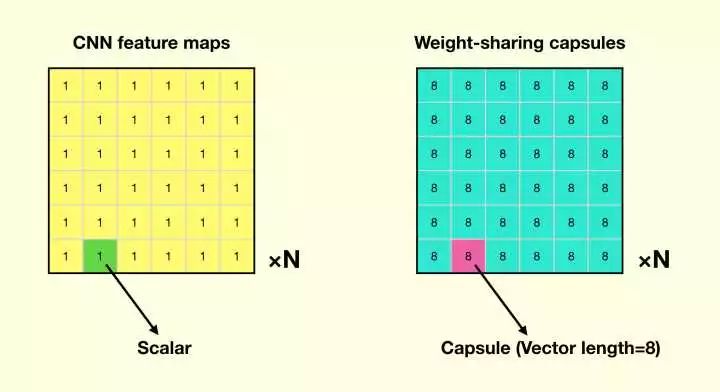
为了加深理解，我们可以对比一下 CNN 的输出和这层输出的 Capsules 的区别:

CNN 的输出，和论文中这层 Capsules 的输出的比较

我们可以看到它们的相似点在于，每个” 平面 “内，变量都是共享权值的；而在不同” 平面 “内，变量是独立的。而不同点在于，在” 平面 “内 CNN 的单位是标量，而 Capsules 是一个 capsule 表征的向量。

这一层的 Capsules 在论文中被称为 PrimaryCapsules ，这让我联想到 primary visual cortex（初级视皮层），因为如果说第一层卷积相当于视网膜，第二层卷积相当于初级视皮层，那么 PrimaryCapsules的向量就是初级视皮层的表征。

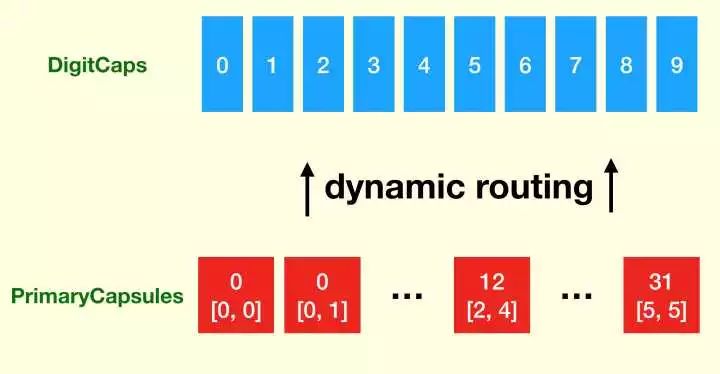
第三层，也是输出层，就是一组 10 个标准的 Capsules，每个 capsule 代表一个数字。每个 capsules 输出向量的元素个数为 16。这组 Capsules 被称为 DigitCaps （取名逼死强迫症）。

从 PrimaryCapsules 到 DigitCaps 使用了上文所述的 dynamic routing。这也是唯一使用 dynamic routing 的地方。

从 PrimaryCapsules 到 DigitCaps

按照假定，某个 capsule 输出向量的 (范数) 长度表示某个 capsule 表征的内容出现的概率，所以做分类的时候取输出向量的 L2 范数即可。

这里注意到，最后 capsules 输出的概率向量不是归一的，也就是 capsules 天然有同时识别多个物体的能力。

分类任务：最后取 DigitCaps 向量的 L2 范数

  优化

由于 capsules 允许多个分类同时存在，所以不能直接用传统的交叉熵损失，一种替代方案是 SVM 中常用的 margin loss:

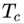
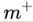
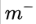
其中 c 是分类， 是分类的指示函数（分类 c 存在为 1，否则为 0）， 为上 margin，惩罚假阴性（没有预测到存在的分类的情况）； 为下 margin，惩罚假阳性（预测到不存在的分类的情况）。 λ 是比例系数，调整两者比重。

总的 loss 是各个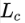 之和。

至于优化算法，论文没有明说，其实不难猜到就是标准的反向传播（否则怎么搞 CNN），估计作者觉得没有必要写了。论文在很多细节上让人很难受，比 AlphaGo Zero 的文笔差多了（人家把讲过 N 次的 MCTS 还是换个说法耐心地讲解了一遍）。

  重构与表示

Hinton 一直坚持的一个理念是，一个好的 robust 的模型，一定能够有重构的能力（” 让模型说话 “）。这点是有道理的，因为如果能够重构，我们至少知道模型有了一个好的表示，并且从重构结果中我们可以看出模型存在的问题。

之前我们说过，capsule 的一个重要假设是每个 capsule 的向量可以表征一个实例。怎么来检验这个假设呢？一个方法就是重构。

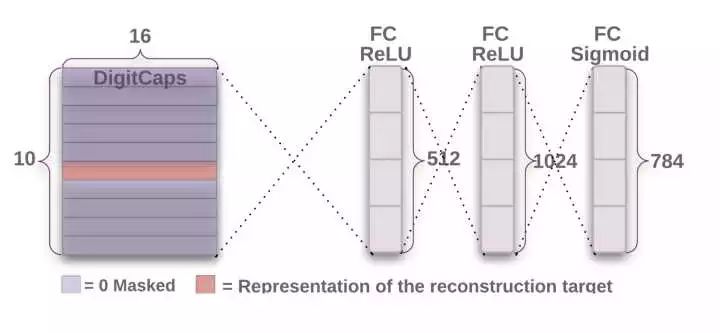
重构的时候，我们单独取出需要重构的向量，扔到后面的网络中重构。当然后面的重构网络需要训练。

重构模型

但是有读者可能会有疑问：如何证明重构的好是因为 Capsules 输出了良好的表示，而不是因为后面的网络拟合的结果？我们知道哪怕前面的输入是随机的，由于神经网络强大的拟合能力，后面的网络也能拟合出重构结果。

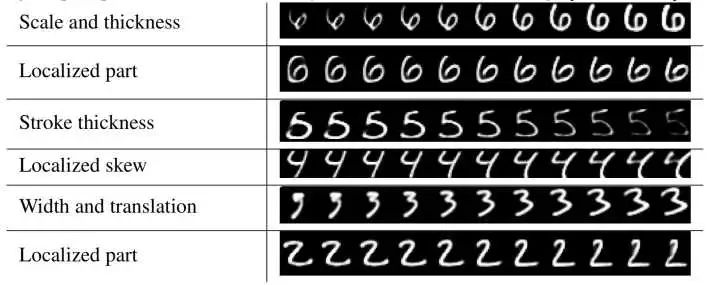
一个证据是人为扰动 capsule 的输出向量。我们可以看到，如果逐渐改变向量的一些分量，表示也很有规律地改变，这是随机的输入难以做到的。

通过扰动 capsule 的向量，产生不同效应的重构结果

另外，他们没有拿 capsule 的输出向量做个 t-SNE，这点很可惜。。。如果这样我们就能看到 capsule 的输出向量是如何把 MNIST 嵌入到空间中去的。

  重构与无监督学习

论文中发现如果把重构误差计入，可以显著地提高准确率：

有重构介入时，准确率有显著提升

（其实很搞笑的是，这种提升远远大于对 dynamic routing 的调整）

需要注意到，重构是无监督的方式，不需要标签。如果重构能够大幅提升分类效果，那么就暗示了可以通过重构做无监督学习（重构也可能是人做无监督学习的途径之一）。这部分 Hinton 提了很多，应该已经做出来了，不过看样子不在这篇论文当中。

  重构与可解释性

之前我在 [2] 中简单提及过，做 capsule 的动机之一还在于可解释性。我们需要看到 NN 为什么正确，为什么错误。

这篇论文通过重构或多或少这一点，还是很有意思的。

比如下图左侧，都是分类正确的重构，可以看到重构除了还原本身外，还起到了去噪的效果。

右侧模型误把”5“识别成了”3“，通过重构，模型” 告诉 “我们，这是因为它认为正常的”5“的头是往右边伸出的，而给它的”5“是一个下面有缺口的”3“。

对正确和错误的分类进行重构

在识别重叠数字的时候，它显示了更强的重构能力，并且拒绝重构不存在的对象（右侧 * 号）

识别重叠数字，以及重构结果

  为什么选择 MNIST 而不是 ImageNet

我知道，大家都会吐槽为什么还要用 MNIST 这种用烂的数据集。

首先是，ImageNet 很难做重叠图像的实验（现实图片重叠的情况下本来就很难辨认，即使实现了也很难可视化），这点手写数字几乎是最理想的方案。

第二点是，在此实验的配置下，做 ImageNet 是自杀行为。因为 Capsules 假设是每个 Capsule 能够代表一个实例，本论文实现的动态路由方案比较 naive，根本不能满足这么多的 Capsule 数量，何必做不符合自己假设的实验呢？其实文章作者知道这点，还是强行试了试 cifar10，果然效果不好（和最初应用到 cifar10 的 CNN 效果差不多）。

  另外一个关键的数据集： smallNORB

Capsule 非常重要的卖点是符合图形学的某些现象（参见 [2]）， 在 smallNORB 上达到 state-of-the-art 是非常重要的支持。

smallNORB 数据集

smallNORB 和 MNIST 一样，构成非常简单，所以目前的 CapsNet 架构可以训练。但是 smallNORB 非常重要的一点是，它是 3D 的，并且明显由各个组件构成的，这点对于 Capsules 是非常有利的（如果 Capsules 假设正确）。

我相信以后关于 Capsules 的论文中 smallNORB 可能还会出现多次。

  全场最差：动态路由

个人认为动态路由是论文中做的最不好的地方，做的太简单了，如果用论文中的动态路由方案，我想是无法做到训练 ImageNet 的。

按照 Capsules 的假设，在当前方案下，训练 ImageNet，估计至少要用长度 100 的向量来表征一个物体吧（可能还是不够）。假设我们卷积层保持 256 * 256 的长宽，256 个独立的 Capsules 分组，那么一层就有 16777216 个 Capsules，我们不管其他的，就看最后输出 1000 个分类，需要 1000 个 Capsules（假设向量长度还是 100 个元素），那么参数占用内存（设类型为 float32）就是 16777216 * 1000 * （100*100*4）= 671088640000000 = 671.08864 TB（不计路由等部分）。实际训练中内存还会数倍于这个数字，至少要翻一倍，到 1.7 PB 左右。如果你要单独用 GPU 放下这一层，就需要 80000 张 Titan X Pascal，更别提整个网络的参数量。如此多的参数显然是因为全连接的动态路由造成的。

相信路由方案一定是将来改进的重点。

关注 AI 研习社，回复【论文】即可获取论文原文及翻译。

[1] Hinton, G. E., Krizhevsky, A., & Wang, S. D. (2011, June). Transforming auto-encoders. InInternational Conference on Artificial Neural Networks (pp. 44-51). Springer Berlin Heidelberg.

[2] 浅析 Hinton 最近提出的 Capsule 计划

新人福利

关注 AI 研习社（okweiwu），回复  1  领取

【超过 1000G 神经网络 / AI / 大数据，教程，论文】

全文翻译 Hinton 那篇备受关注的 Capsule 论文 

▼▼▼