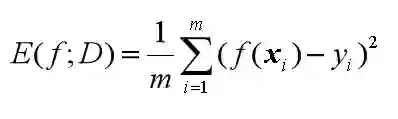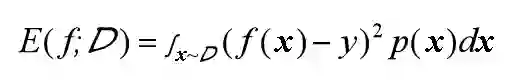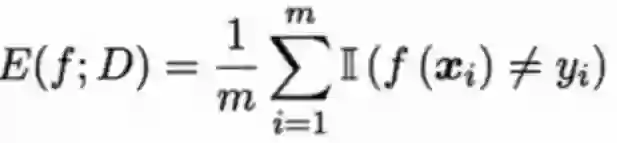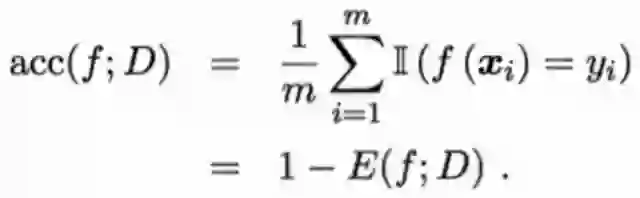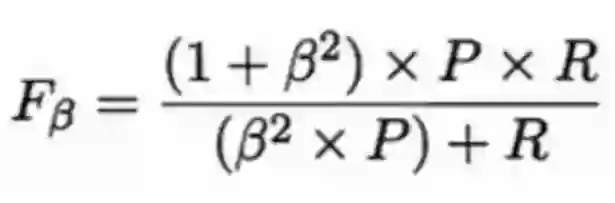干货|【西瓜书】周志华《机器学习》学习笔记与习题探讨（二）②

西瓜书系列笔记

干货|Coursera吴恩达《神经网络与深度学习》课程笔记（1）-- 深度学习概述

干货|Coursera吴恩达《神经网络与深度学习》课程笔记（2）-- 神经网络基础之逻辑回归

1

性能度量

首先重温一遍理想。

理想：通过评估学习器的泛化误差，选出泛化误差最小的学习器。

那么，上一节通过留出法、交叉验证法和自助法得到了可以表现泛化误差的测试误差后，如何选出表现最佳的学习器呢？这就需要对泛化能力有一个评价标准。简单举个例子就是：得到了值，带入标准之中，选出最终结果。

【性能度量】：衡量泛化能力的评价标准。

但实际上的性能度量，还要反映任务需求。在对比不同学习器的能力时，使用不同的性能度量往往会导致不同的评判结果。什么样的学习器是好的，不仅取决于算法和数据，还决定于任务需求。

预测任务中，评估学习器f的性能，需要将学习器的预测结果f(x)同真实标记y进行比较。

所以现在主要讨论的是监督学习。

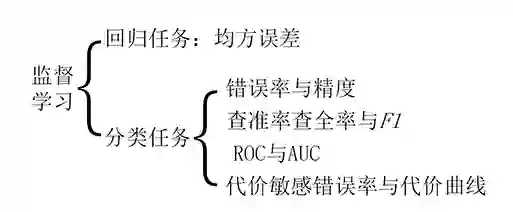
如图是监督学习的性能度量，其中回归任务的性能度量一般采用均方误差，而分类任务的性能度量多种多样。

1、回归任务的性能度量——均方误差：

公式如下：

可知，均方误差是m个离散样本的方差的平均数。

但对于数据分布Ɗ和概率密度p(·)，均方误差的计算公式如下：

可知，此时样本可以看做非离散样本而是连续样本。

性能度量方法：通常，均方误差大的模型性能差，均方误差小的模型性能好。

均方误差反应的是回归任务模型判断正确与否的能力。

2、分类任务的性能度量1——错误率与精度

错误率：分类错误的样本占样本总数的比例。

精度：分类正确的样本占样本总数的比例。

错误率是m个离散样本的指数函数和的平均数。

精度与错误率相同，也是m个离散样本的指数函数和的平均数，但两者的指数函数不同。

但对于数据分布Ɗ和概率密度p(·)，错误率和精度的计算公式如下：

可知，此时样本可以看做非离散样本而是连续样本。

性能度量方法：通常，错误率低精度高的模型性能好，错误率高精度低的模型性能差。

错误率与精度反应的是分类任务模型判断正确与否的能力。

3、分类任务的性能度量2——查准率、查全率与F1

当需要反应的不是判断正确与否的能力，而是正例、反例查出的准确率时，就不能用错误率和精度作为判断分类任务模型的性能度量了。

判断得是否正确，在二分类任务中有四种表现形式，还拿西瓜🍉举例：

好西瓜判断成好西瓜，判断正确①；好西瓜判断成坏西瓜，判断错误②；

坏西瓜判断成好西瓜，判断错误③；坏西瓜判断成坏西瓜，判断正确④；

其中，①和④都是判断正确，②和③都是判断错误。错误率和精度是①和④、②和③的综合判断，只有判断正确与否的概念，没有正例反例的区别。

所以要引入查准率（P）、查全率（R）的概念。

下表是二分类结果混淆矩阵，将判断结果分为四个类别，真正例（TP）、假正例（FP）、假反例（FN）、真反例（TN）。

查准率：【真正例样本数】与【预测结果是正例的样本数】的比值。

查全率：【真正例样本数】与【真实情况是正例的样本数】的比值。

查准率是在讲，挑出的好瓜里头，有多少真的是好瓜。所以当希望选出的好瓜比例尽可能高的时候，查准率就要高。（当瓜农面对零售时，会逐个判断哪一个是好瓜，然后对每一个顾客说：“保校保甜，不甜不要钱。”如果瓜农的查准率不高，他要赔死了。）

查全率是在讲，挑出来真的好瓜，占总共好瓜个数的多少。所以当希望尽可能多的把好瓜选出来的时候，查全率就要高。（当瓜农面对批发时，就不要求每个都甜了，尽可能多的把好瓜都挑出来就行了，不然就浪费了好瓜。）

一般来说，查准率高时，查全率偏低；查全率高时，查准率偏低。通常只在一些简单任务中，查准率和查全率都偏高。

性能度量的方法：1、直接观察数值；2、建立P-R图。

直接观察数值已经介绍过了，现在介绍P-R图。

P-R图，即以查全率做横轴，查准率做纵轴的平面示意图，通过P-R曲线，来综合判断模型的性能。

但值得一提的是，同一个模型，在同一个正例判断标准下，得到的查准率和查全率只有一个，也就是说，在图中，只有一个点，而不是一条曲线。

那么要得到一条曲线，就需要不同的正例判断标准。

在判断西瓜好坏的时候，我们不是单纯的将西瓜分成好坏两堆，左边一堆好瓜，右边一堆坏瓜。

而是对预测结果进行排序，排在前面的是学习器认为最可能是正例的样本，排在最后面的是最不可能的样本。

现在按顺序，依次将每一个样本划分为正例进行预测，就得到了多组查准率和查全率的值了。

多组值就是多个点，样本充足的时候，可以连成一条平滑的曲线，即为P-R曲线。

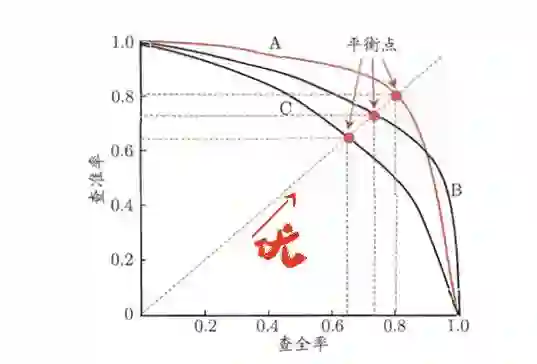
得到P-R图后，如何判断哪个学习器性能更佳？

当曲线没有交叉的时候：外侧曲线的学习器性能优于内侧；

当曲线有交叉的时候：

第一种方法是比较曲线下面积，但值不太容易估算；

第二种方法是比较两条曲线的平衡点，平衡点是“查准率=查全率”时的取值，在图中表示为曲线和对角线的交点。平衡点在外侧的曲线的学习器性能优于内侧。

第三种方法是F1度量和Fβ度量。F1是基于查准率与查全率的调和平均定义的，Fβ则是加权调和平均。

通过比较两条曲线的F1，来判断哪个学习器性能更好。

但在不同的应用中，对查准率和查全率的重视程度不同，需要根据其重要性，进行加权处理，故而有了Fβ度量。β是查全率对查准率的相对重要性。

β>1时：查全率有更大影响；β=1时：影响相同，退化成F1度量；β<1时：查准率有更大影响。

以上是一个二分类混淆矩阵的查准率和查全率判断。

但实际情况中，一个分类学习器往往并不只有一个二分类混淆矩阵，当多次训练/测试或是在多个数据集上进行训练/测试的时候，就会出现多个二分类混淆矩阵。当需要综合考虑估计算法的“全局性能”时，有两种解决办法。

宏：在n个混淆矩阵中分别计算出查准率查全率，再计算均值，就得到“宏查准率”、“宏查全率”和“宏F1”。

微：先将n个混淆矩阵的对应元素进行平均，再计算查准率查全率和F1，就得到“微查准率”、“微查全率”和“微F1”。

4、分类任务的性能度量3——ROC与AUC

与P-R图相同，ROC图通过对测试样本设置不同的阈值并与预测值比较，划分出正例和反例。再计算出真正例率和假正例率。P-R图逐个将样本作为正例，ROC图逐次与阈值进行比较后划分正例。本质上，都是将测试样本进行排序。

真正例率（TPR）：【真正例样本数】与【真实情况是正例的样本数】的比值。（查全率）

假正例率（FPR）：【假正例样本数】与【真实情况是反例的样本数】的比值。

ROC图全名“受试者工作特征”，以真正例率为纵轴，以假正例率为横轴。

转自：机器学习算法与自然语言处理

完整内容请点击“阅读原文”