如何科学地踢好一场足球赛
来源:数学模型
本文约3838字,建议阅读8分钟
引言
足球,被誉为“世界第一运动”,是全球体育界最具影响力的体育运动。现代足球起源于我国古代的蹴鞠。蹴鞠始于战国时代,在唐朝开始盛行 [1]。几乎所有的男人都踢过足球,所有女人也都看过男人踢足球。标准足球比赛由两队各派 11 名球员在长方形的草地球场上对抗、防守、进攻。比赛时尽量将足球射入对方的球门中,每射入一球得一分。比赛结束时,得分多的一队胜出 [2]。

虽然足球起源于我国,但我国国足水平却很一般。国足与世界的差距始于儿童和青少年的足球培养。图 2 是各国小孩的足球活动,中国的足球操只耍不踢,老外都看傻眼了。

足球是一项团队运动,想要赢得比赛,球员必须相互配合。图 3 所示的是不太懂得相互配合的机器人足球赛。
一个优秀的球队,绝不是个人英雄主义者的球队,而是团队协作、默契配合地相互传球和进攻。那么如何从数据上定量描述团队协作、默契配合程度呢?图论或网络模型已经被成功用来研究涉及球员之间传球的团队运动。本文的目的是以实际案例说明如何运用网络理论来分析团队运动的统计信息,并给出提高团队胜率的建议。
模型
数据
本文建立网络模型所使用的数据来自文献 [3,4]。数据包含了哈士奇足球队整个赛季与 19 个对手球队的 38 场比赛数据(哈士奇与每个对手球队进行两场比赛)。数据涵盖了 366 名球员(30 名哈士奇球员, 336 名对手球员)之间的 23429 次传球,以及 59271 场比赛。数据包括比赛场次、球队编号、每次传球接球的队员编号和坐标、传球方式、传球时间。具体数据格式见附录 A。
网络模型
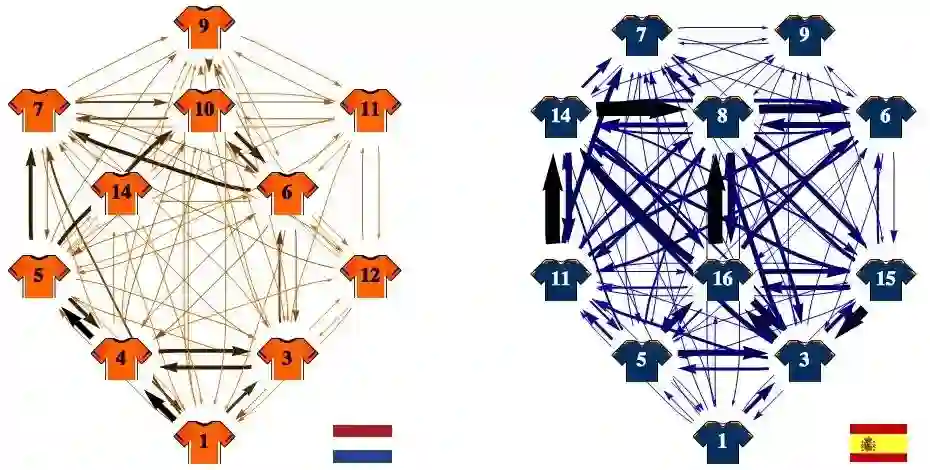
我们可以将每场比赛中的任意一个队一段时间内的传球定义为一个网络,该网络将以球员作为节点,球员间的传球作为边,并根据两球员之间成功完成的传球次数作为边的权重。图 4 为 2010 世界杯半决赛时荷兰队对战西班牙的传球网络,图 5 为 三名球员构成的传球网络及其邻接矩阵。

本文参考文献 [6] 中的方法,以 100 次传球为一个网络单元,研究一段时间内传球网络的变化过程。第 1 次传球至第 100 次传球的时间段称为 ,对应的传球网络为 ,第 2 次至第 101 次传球的时间段称为 ,对应的传球网络为 ,依此类推,每次都是在上一个传球网络的基础上,去掉起始的传球,加入新的传球。选择 100 次传球作为网络单元的原因是:
-
通过测试,发现以 100 次传球为单元,可以使每一次的传球网络都包含 11 个球员,如果传球网络中纳入的传球次数太少,在网络中就会出现球员不完整的情况。 -
在保证网络包含所有球员的前提下,应该尽量减少网络中的传球次数,增大样本量,使结论更加可靠。
值得注意的是,在比赛过程中,存在替换队员的情况,本文主要研究网络,因此在队员替换后,新队员的数据仍然看作旧队员的。本文以哈士奇足球队的第一场比赛为例,模拟比赛球员之间传球网络随时间的变化过程,结果如图 6 所示。
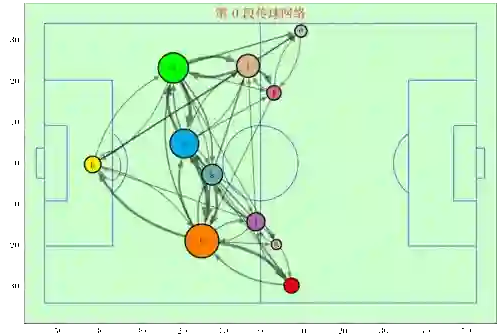
图中,11 个节点别代表 11 个球员,节点半径大小由球员的总接传球次数决定,节点坐标为球员在传球时的平均坐标。两节点间的弧(有向的边)表示两节点间存在传球,弧的方向表示传球的方向,弧的粗细表示传球次数。
网络参数
为了探究传球网络与比赛结果的关系,需要量化传球网络的参数。本文选取集聚系数、球队进攻节奏、 球员紧密系数 [6] 作为传球网络的参数进行研究。
集聚系数
节点的局部集聚系数是用来描述该节点在图中与其它节点之间结集成团的程度。具体来说,是一个点的邻接点之间相互连接的程度。通常节点 的局部集聚系数可由直接连接到节点 的节点数量百分比来表示。该测度可以对网络的 个节点求平均得到平均聚类系数。然而,当网络为加权有向时,我们不能简单地计算它们之间连接的节点数。传球网络正是这种例外的情况:球员对之间的传球次数不是恒定的。本文使用以下加权集聚系数度量 球员与其他球员的之间的连接程度 [6]:
其中 和 是球队的任意其它两名球员, 和 是球员 和他们两人之间的传球次数。值得注意的是,加权集聚系数表征了队员之间形成三元结构的趋势。在球队进攻时,需要队员之间的配合,通常会存在两种队形,一种是两个队员互相传球,另外一种是三个队员互相传球,分别称为二元和三元结构。最后,再计算所有球员 的平均值得到整个网络的集聚系数:
集聚系数越高,说明球队形成三元结构进攻的趋势就越强 [7]。
进攻节奏
球队的进攻节奏也会影响到球队的得分。本文用传球距离在接近对方球门的有效程度来表示进攻节奏。当传球发生时,传球和接球球员的 坐标差 是球接近对方球门的有效距离,而 坐标差 则是无效距离。因此可对进攻节奏做如下定义:
紧密系数
在传球网络中,最短路径长度 是球从一名球员传到另一名球员必须经过的最少球员数。由于传递网络是加权的(即球员之间的传递次数不同),我们必须考虑到路径的不同权重,考虑到权重越高,两个节点之间的拓扑距离越短。球员 和 之间的拓扑距离被定义为路径权重的倒数 。对于加权网络,两个球员之间的最短路径长度可能不是两者之间的直接连接,我们使用 Dijkstra 算法计算所有对球员之间的最短最短路径 。再利用下式计算出球队网络的平均最短距离。
平均最短距离越短,说明球员传球时联系越紧密,配合得越好。
结果
传球网络参数随时间的变化
集聚系数:为了研究一段时间内球队以三元结构进行进攻的趋势,本文先选取哈士奇第一场比赛的数据作为研究对象。结果如图 7 所示。由图可以看出,在 至 时,哈士奇球队的三元结构趋势明显大于对手 1。由于哈士奇球队和对手球队的传球次数不一样,在这里取两个球队相同的段数作比较,例如,在第一场比赛中哈士奇有 269 段,对手球队有 98 段,此处截取哈士奇球队的前 98 段和对手作比较。计算集聚系数的程序见附录 B 代码 1 和代码 2。
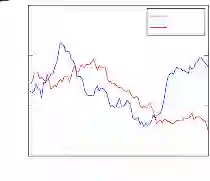
进攻节奏的计算结果如图 8 所示,程序见附录代码 3。从图可以看出,哈士奇球队的 明显高于对手,也就是说哈士奇踢的比较稳,节奏比较慢。
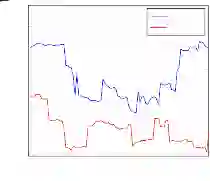
紧密系数:在计算球员之间的最短路径时,发现了以 100 次传球为单位的弊端,即某些球员在 100 次传球内没有接到过传球,只是传出了一次球,因此在计算紧密系数时,本文将网络单元从 100 次传球调整为 150 次。计算结果如图 9 所示,程序见附录代码 1。
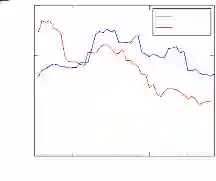
平均最短路径越短,说明队友间联系越紧密,可以看出,哈士奇在前期的时候队友间的联系比对手好,但是在 15 段之后远高于对手,这说明在中后期哈士奇球队的传球配合得不是很好。
38 场比赛数据对比
上文中以第一场比赛为例,得到了比赛过程中参数值的变化情况。本节,我们将计算 38 场比赛的参数值,此处的参数值为每场比赛的平均值,而不是之前的 100 次传球的平均值。
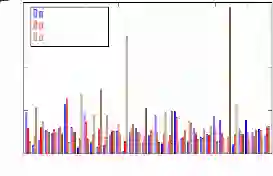
为方便比较 38 场比赛哈士奇球队与对手球队的参数值,并研究这些参数值是否与胜负相关,因此计算哈士奇球队和对手球队参数的比值:
其中, 为哈士奇的集聚系数, 为对手的集聚系数, 为哈士奇与对手的集聚系数比值,其余参数的定义同理,不再赘述。计算出 38 场比赛哈士奇与对手球队参数值的比,如图 10 所示,程序见附录代码 4。当 值大于 1 时,说明哈士奇的参数值大于对手,图 10 不能明显的看出各场比赛参数值的区别。为了研究这些参数值与比赛胜负的关系,本文求出不同了比赛结果的参数值,具体如图 11 所示。
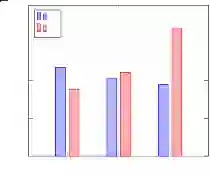
从图中可以看出,哈士奇获胜时的 值明显要低于失败时的值,而 值相差不大, 获胜时的值高于失败时的值。这说明如果想要获胜,需要提高球队的 值,降低 值,即尽量采用三元结构进攻,并提高球员之间的联系紧密度。通过独立样本检验比较不同比赛结果的参数值是否具有显著性差异,结果如表 1 所示。
| 参数比值 | 胜负 | 个案数 | 平均值 | 显著性 |
|---|---|---|---|---|
| 集聚系数 | 失败 | 15 | 0.89 | 0.16 |
| 胜利 | 13 | 1.18 | ||
| 进攻节奏 | 失败 | 15 | 1.11 | 0.58 |
| 胜利 | 13 | 1.03 | ||
| 紧密系数 | 失败 | 15 | 1.70 | 0.09 |
| 胜利 | 13 | 0.95 |
结论
通过分析哈士奇整个赛季的 38 场比赛,对比其获胜时和失败时数据的差异,得到以下结论:
-
应该注重提高队友之间的传球配合,足球是一个团队游戏,不只是一两个人的球技秀。 -
三元结构(三个人互传的进攻队形)次数多的球队往往更容易获胜。 -
球队进攻节奏的快慢对比赛的结果没有显著的影响,说明比赛时不需要刻意的放慢进攻节奏。
附录
附录较长,公众号内回复“足球网络”下载所有文件。
参考资料
FIFA. History of football: http://www.fifa.com/classicfootball/history/the-game/origins.html
[2]足球 - 维基百科: https://zh.wikipedia.org/wiki/足球
[3]Luca Pappalardo, Paolo Cintia, Alessio Rossi, Emanuele Massucco, Paolo Ferragina, Dino Pedreschi, and Fosca Giannotti. A public data set of spatio-temporal match events in soccer competitions. Scientific data, 6(1):1–15, 2019.: https://google.com
[4]MCM 2020 problems: https://www.comap.com/undergraduate/contests/mcm/contests/2020/problems
[5]Javier López Peña. A network theory analysis of football strategies, 2012: https://www.groundai.com/project/a-network-theory-analysis-of-football-strategies/1
[6]Busquets J. Echegoyen I. et al. Buldú, J.M. Defining a historic football team: Using network science to analyze guardiola’s f.c. barcelona. Sci Rep, 9(13602), 2019: https://google.com
[7]Cotta Carlos, Antonio M Mora, Merelo Juan Juli N, and Merelo Molina Cecilia. A network analysis of the 2010 fifa world cup champion team play. Journal of Systems Science & Complexity, (1):24–45.: https://google.com
——END——


