《三体》文明的进击

2019 年 12 月 29 日 新智元

新智元推荐

来源：老顾谈几何作者：顾险峰

【新智元导读】《三体》中，刘慈欣对于人性的预言非常悲观，描述的末世场景令人毛骨悚然。但是，又有谁能够确定或者否定：黑暗森林中三体人正在觊觎地球，“智子”在人间！现在戳右边链接上新智元小程序了解更多！

《三体》，中国科幻史上里程碑式的作品，刘慈欣用恢弘瑰丽的想象，为世人揭示了文明存亡的“黑暗森林”法则，鞭挞了人性的短视和丑陋，彰显了只有基础科学才能拯救人类的主题。生活在三体世界中不断进化和毁灭的三体人，掌握了超越地球文明的科学水准。他们的星系漂浮着三个恒星，其轨迹混沌而不可预测，时刻有可能将三体人的行星吞噬。三体人无时无刻不希望逃离灭顶之灾，殖民其他星系。他们截获了人类对太空发射的信号，从而开始了对地球文明的进击，旨在一举消灭地球人类，通过移民取而代之。在严酷冷峻的博弈中，人类只能仰仗严格冷静的逻辑，领悟到黑暗深林法则，建立了同归于尽的威慑系统，与三体人维系了脆弱而短暂的和平。在主流文艺作品中，人性的博爱往往是对抗科技暴力的终极手段。但是在大刘的笔下，人性的温情与博爱却成为葬送人类文明的罪魁祸首。最终脆弱的平衡被颠覆，借助黑暗森林中藏匿的高等文明，人类和三体人相互毁灭了对方的文明。

刘慈欣，科幻作家。《三体》、《黑暗森林》、《死神永生》作者。

《三体》文风冷峻严酷，通篇都是三体人运用人性的弱点，对人类的压制和屠戮。当人类寄希望于宇宙中高级文明来主持正义之时，黑暗森林法则将最后的希望无情扼杀，人类只能依靠自身的科学发展而自救。整个故事压抑阴郁，结局黑暗，名为科幻小说，实为批判现实主义的力作。大刘用《三体》的故事，警醒世人，由于黑暗森林，文明间的博弈较量无可避免，终极对抗的是科学水准。中华民族自古强调实用主义，能工巧匠无数，创造了璀璨的技术文明。但是，古人一直关注具有直接应用价值的技术发展，对技术背后深刻的机理缺乏探究，因此文化中缺乏科学探索的精神，近代饱受列强的欺辱。对此，大刘进行了深刻的反思。在《三体》中，三体世界为了保证顺利向地球移民，消灭地球社会和人类，开发了“智子”技术，将单个质子从九维展开成二维，并雕刻成超级计算机。“智子”被发送到地球，干扰人类高能物理实验，将人类的科学研究锁定，使之停滞不前。与之相反，“智子”并没有锁定技术，使人类沾沾自喜于技术的提高，麻醉于物质享受之中。这里，大刘犀利地指出，阻碍一个文明发展的关键在于阻碍其基础科学的发展，而非其技术的发展。

在老顾的科研教学生涯中，见过太多的关于追求基础科学还是实用技术的争论。

拖拉机驾驶 vs. 微积分

二十多年前，老顾到哈佛求学。到达实验室第一天，老顾向芒福德教授（David Mumford，代数几何学家，计算机视觉学家，菲尔兹奖得主）求教。芒福德给老顾讲解了美国民众对于科学发展的态度转变。在国力鼎盛之前，美国的科学水准长期低于欧洲。当时美国的经济强烈依赖于农业，绝大多数人民没有上大学的能力和意愿。当时教育界关于高中课程设置曾经展开过激烈的争论。很多人认为应该传授学生现代数学的基本知识，特别是微积分；更多的人认为微积分距离学生的现实生活太远，应该教授学生切合实际的谋生技术，拖拉机驾驶技术。因此，美国民众对于基础科学一直缺乏了解，更没有内在的热情。

但是，第二次世界大战彻底转变了美国民众的科学观。世界大战摧毁了欧洲的经济体系、工业体系。本来重商主义盛行的美国希望侧身事外，坐享渔翁之利。但是由于珍珠港事件，美国不得不倾尽国力应战。当时传统的战争武器主要是依赖物质的化学能，坦克机枪，航母飞机代表了科技水准。爱因斯坦揭示了质能关系，预言了核武器的诞生。他富有远见地提出要在纳粹德国之前研发出原子弹，提议获得了时任总统罗斯福的支持，因此开展了曼哈顿计划。在战争后期，面对日本被军国主义挟持的举国狂热，美国用原子弹结束了战争。在各个民族生死存亡的战争中，一锤定音的是科技。而原子科学的起因并不是商业利益，也不是民粹精神，而是人类特有的好奇心，对于自然理解的精神追求。从此，美国民众对于核物理等基础科学从冷漠怀疑，转向积极支持。

老顾的教学科研生涯主要在计算机科学领域，除了计算机科学的算法，老顾也非常重视向学生传授一些现代几何和拓扑的知识。每门课的期末阶段，老顾都会讲解一些基于现代几何发展的计算机算法，例如Ricci流、最优传输，及其在计算机科学中的应用。据老顾观察，令人遗憾的是，绝大多数的计算机学生都非常注重谋生技能的学习，例如各种深度学习的算法（驾驶拖拉机），而对于其背后的理论基础（微积分）缺乏好奇心，更有学生对此嗤之以鼻，摔门而去。有很多非常有天赋的博士生，包括很多纯粹数学专业的学生，执着于用对抗生成网络生成人脸表情、用计算机动画模拟自然现象等直观刺激的研究项目，对于深刻思考基础理论缺乏信心和兴趣。

核物理的遗产

在上个世纪八十年代，物理科学的发展极大地激励了年轻人投身到基础物理研究的领域。李政道先生的CUSPEA项目，吸引了中国众多有才华的年轻人来到美国深造物理。虽然这批物理学者最终留在物理领域的非常少，但是他们很多人都用核物理的知识在医学领域大展宏图。老顾的很多朋友都是CUSPEA的受惠者。在他们学业完成之际，理论物理的热潮衰退，但是核医学领域蓬勃兴起。计算机断层扫描（CT）和核磁共振（MRI）技术大放光彩，放射治疗技术，一日千里，势不可挡，彻底革命了医疗技术。目前的医疗诊断非常倚重各种医学图像技术，而这些技术的发展都是依赖于理论物理的基础。

石溪大学有着悠久的医学图像科研传统。石溪的Paul Lauterbur教授是核磁共振技术的主要发明者。老顾经常和放射学的合作者们讨论科研项目，他们都是当年CUSPEA培养的物理学家，目前在医疗图像领域颇有建树。每当谈到CT图像的重建，老顾总是力图从拉东变换的几何图景入手，朋友总是从粒子的物理特性入手。由此可见朋友的思维方法来自于严格的物理训练。

老顾也有朋友在斯隆-凯瑟琳癌症中心从事放射医疗工作，每天都诊治很多病人。这位朋友具有相似的CUSPEA物理背景，毕业于斯坦福大学的加速器专业。他的治疗室中有一台巨大的电子加速器，用于放射治疗，轰击癌症细胞。由于常年处于高辐射的环境，朋友终年戴着一副深色墨镜，即便在室内也不会摘下。每次闯过厚厚的铅制大门，来到肃穆惨白的治疗室，空气中弥散着消毒液的味道，四周巨大的加速器辅助设备发出嗡鸣。朋友身着白色大褂，戴着墨镜，面无表情地拍打着加速器，幽幽地对老顾讲：“所有的人，最终的结局都在这里。”每次老顾仓惶离开那里的时候，都会思考生命的意义：生命如此短暂，结局如此凄惨，如何才能真正留下些超越时代的东西？

无用之用

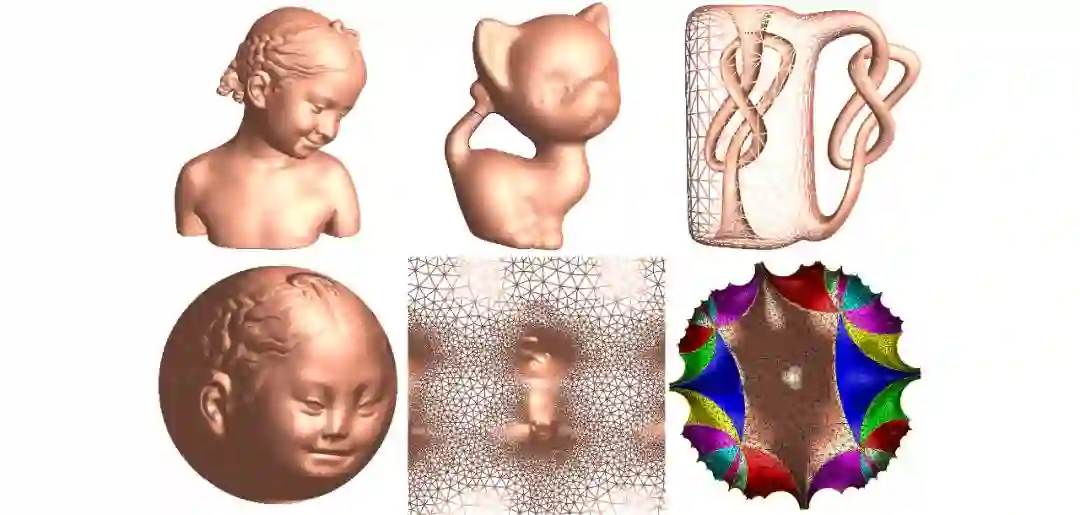
老顾和放射学界的朋友们常年致力于研究虚拟肠镜技术。人过中年之后，每年肠道中都会长出一些息肉。息肉以每年一毫米的速度生长，达到一定尺寸之后，会由于摩擦而发生溃疡。在修复表皮溃疡的过程中，细胞DNA会被频繁复制，容易发生一些错误。错误积累到一定程度，会发生突变，从而形成癌症。由于肠道缺乏神经，病人一旦发现某些症状，那么往往已经到了晚期。最为有效的防治直肠癌的方法是用肠镜进行内窥检查，将有可疑的息肉直接剪出。传统的肠镜检查方法非常具有侵犯性，需要将患者全身麻醉，将光学设备探入肠道。如果操作不当，容易发生并发症。特别是，肠壁表面有很多皱褶，传统的光学方法无法看到藏在皱褶里的息肉，从而漏检。虚拟肠镜技术和病人没有肢体接触，用医学图像技术扫描其腹部，在计算机上复制病人的直肠曲面，并且用现代几何方法将带有皱褶的弯曲肠壁曲面平铺到平面上，保持局部形状不变。这一方法不需要对病人麻醉，不会产生并发症，同时所有皱褶大开，所有息肉无所遁形。同时，这一技术不需要医生手工操作，简便经济。这里将曲面保形摊平的核心技术是来自于近期拓扑学方面的一个突破：庞加莱猜想的证明。

虚拟肠镜技术。

庞加莱猜想是基于如下的一个简单观察：球面上任何一条封闭曲线，都可以沿着球面逐渐形变，缩成一个点。庞加莱猜想这一命题反过来也对：“如果一个紧致的三维流形中所有的封闭曲线都可以在流形内渐缩成一点，那么这一流形必定是三维球面。”当年老顾初次看到庞家莱猜想，觉得这一问题简直是无病呻吟，如此直观简单的事实居然需要严格证明，纯粹是数学家故弄玄虚的无聊之作。老顾当时无法理解数学家为什么对于如此直观自然的现象要追求严密证明，也无法预见到即便证明了这一猜想又有何用。历经多年的奋战，庞加莱猜想最终用哈密尔顿的Ricci流方法证明。

在庞家莱猜想被证明的时候，老顾的数学修养有所提升，逐渐理解这一数学定理的内在深意。被这一拓扑突破的美学价值吸引，老顾和朋友们试图将这一理论引入到计算机科学领域。大家努力了两三年发展了稳定实用的计算机计算方法，但是无法证明这种方法解的存在性，离散解到光滑解的收敛性。大家又花费了七八年，最终才在数学上给出了严密的证明。证明过程非常漫长，充满挫折和惊喜，很多年都宛若在一条漆黑漫长的隧道中摸索，远处隐约有着微弱的光芒。支撑下来的核心是对自然和谐的坚定信念，和逐渐揭示真相的强烈审美体验，但是一直没有奢望这一方法能够带来任何经济利益。

但是，Ricci流方法最终在工程和医疗领域发挥了重要作用。在工程医疗领域，构造几何体的黎曼度量具有根本的重要性。Ricci流是目前唯一的一种能够通过曲率来构造黎曼度量的方法。例如在虚拟肠镜技术中，将直肠曲面摊平问题等价于构造一个黎曼度量使得其高斯曲率处处为零。虚拟肠镜技术后来转让给西门子公司，从而推广到世界各地。近几年，老顾在国内二三线城市的医院中，经常见到西门子公司的CT扫描设备，里面都配有虚拟肠镜的应用软件。虽然几乎没有人能够理解庞家莱猜想，但是这一无用的冥想所激发的Ricci流方法，已经以令老顾完全意想不到的方式普及到千家万户。联想到这一技术所挽救的生命，单就这一技术而言，其经济回报早就远远超过当年各国政府为拓扑学家所赞助的科研经费总和。老顾的亲身经历说明：如果事先仅从实用角度来评价基础科学命题，则无疑是肤浅而短视的。基础科学的突破，会在技术领域引发雪崩式的连锁反应，从而对于社会实际生活带来连当事人都难以想见的影响。

Ricci流算法用于由目标曲率来构造黎曼度量。

当年，庞加莱猜想的证明非常艰苦卓绝，有很多时候，拓扑学家倾向于认为这一猜想的证明可能是哥德尔所证明的情形：一个命题可以在某个公理体系内描述，但是无法在这一体系内被证明。

被误读的哥德尔

老顾的一位理论班师兄当年研究计算机理论，终生痴迷于哥德尔理论和康托尔连续统假设的证明。无奈时乖命蹇，不情愿堕入商界，但却做得风生水起，在网络领域叱咤风云。财富自由后，追随内心的呼唤，在普林斯顿高等研究所旁购置豪宅，隐居在爱因斯坦和哥德尔生活战斗过的地方。老顾曾经到师兄家拜访。师兄有一个玻璃暖房改成的茶轩，室内四壁山水笔墨，窗外繁花满树，绿草成荫。斜阳暖照，茶香四溢。师兄处黄花梨木的茶具，稚拙典雅，古色古香。师兄拿出自己有关哥德尔、康托尔的学术专著，和老顾一同探讨。

库尔特·哥德尔

希尔伯特曾经希望将数学公理化，哥德尔的理论证明公理化方法比预想的复杂。多年来，很多人用哥德尔的理论来证伪数学各个分支是有机统一的观点，同时也说明人类对数学真理的追求注定是徒劳的，人类不可能真正认识这个世界。从老顾的观点来看，这种似是而非的观点恰恰是对哥德尔理论的最大误解。

哥德尔不完备定理说的是：一个足够复杂的公理体系（至少蕴含了皮亚诺算术公理），如果它是一致的（相容的，无矛盾的），那么它就是不完备的。这里的完备，指的是“对于任何可在这个公理体系内描述的命题，都可以在这个公理体系内得到判定，要么是正确的，要么是错误的”。

哥德尔不完备定理其实有两层意思。第一层是说数学的统一性，即各个分支彼此紧密相连，不可分割，构成一个统一的有机体。一个数学分支的基本问题无法在这一分支中得到证明，但是可以在另外一个分支中被证明；同样，另一个分支中的基本问题无法在自身体系中被证明，但是可以在第三个分支中得以证明。如此，各个分支彼此支撑，彼此依赖，构成复杂的网络。例如，大家都知道代数基本定理：一元多次多项式方程，在复数域中有根。这一代数基本定理可以在代数领域中描述，但是在代数领域中无法证明。代数基本定理却可以在拓扑中证明。上面，拓扑中的基本定理庞加莱定理无法用纯拓扑方法证明，却可以用Ricci流方法证明，Ricci流属于几何偏微分方程。偏微分方程领域中，很多解的存在性证明依赖于拓扑中的不动点理论。但是拓扑中的不动点理论却依赖于代数中的同伦群来证明。我们看到，这些领域的最基本定理的证明往往依赖于其他领域，彼此紧密联系构成一个统一的整体。推而广之，数学和物理之间，自然科学的各个分支之间，也是彼此依存，和谐统一。

哥德尔第二层是说无论一个公理体系多么庞大，总有一个命题无法被证明或证伪。这并不意味“人类不可能认识这个世界”，而是意味着“人类认识世界的过程是无限的”，人类用相对真理来逐渐逼近绝对真理，对自然的认识是日渐深化的。从欧几里得几何，到罗巴契夫斯基几何，到黎曼几何，人类认知领域逐步扩大，对自然的理解日益深刻。

在数学史上，每当人们遇到一个艰深的问题，苦苦求索而无所得时，就会怀疑是否遇到了哥德尔不完备定理所描述的情形。费马大定理被证明前，就被人怀疑是否能够在现有的数学体系之内被证明，直到一名悲剧英雄的出现，历史才得以改变。

谷山丰 vs 中本聪

费马大定理是勾股定理的直接推广：勾方加股方等于弦方，将平方换成高次幂之后，方程没有整数解。费马大定理困扰了数学家三百多年，最后被安德鲁·怀尔斯爵士证明。怀尔斯儿时看到费马大定理，就立志解决这一猜想。经过多年潜心修炼之后，怀尔斯功力炉火纯青，于是躲在普林斯顿的阁楼上，闭关屠龙。证明的过程跌宕起伏，几经磨难，在涕泪纵横中，怀尔斯修成正果，风光无限。但实际上，怀尔斯只证明了谷山-志村猜想的一个特例就证明了费马大定理。相比于费马大定理，谷山-志村更为触及数论中心，这一猜想指出，所有的椭圆曲线都有模形式的参数表示。

谷山丰在28岁的时候提出了猜想，虽然石破天惊，但是因为过于不可思议，当时没有人承认它。谷山丰虽然洞悉了自然的真理，但是无法证明自己的猜想，精神痛苦，于31岁时自戕。曾经承诺追随他一生的未婚妻也自杀随他而去。这一对理想主义者的离世迅速被人遗忘。26年后，格哈德·弗赖把谷山-志村猜想和费马大定理联系了起来。并且通过反证法证明了如果谷山-志村猜想成立，那么费马大定理只是作为结论直接可以推出，肯·里贝特进一步完善了细节。怀尔斯最终证明了谷山-志村猜想的特例，从而完成费马大定理的证明，那时距离谷山丰离开人世已经36年了。

费马定理的证明极大地激发了人们对于椭圆曲线理论的兴趣，同时推动了椭圆曲线加密技术的蓬勃发展。而椭圆曲线加密技术是中本聪提出的比特币协议和区块链技术的基础。目前，区块链技术发展得如火如荼，未来有可能重塑人类社会的金融体系。我们再一次看到基础科学对于社会实践的推动作用。

另一方面，比特币技术的兴起迅速引爆了人性的贪婪。在资本市场上，大佬们妙手空空，通过“收割韭菜”就积蓄了百亿身家。对于个人而言，每个人都希望成为币圈大佬，依靠新兴技术聚敛财富，每个人都不希望成为谷山丰式的悲剧英雄，为了拓展人类的知识疆域而殉道。但是对于整个民族、整个文明而言，真正的推动力量还是来自谷山丰们。如果每个公民都心甘情愿地缴纳智商税，成为生生不息的韭菜，并且千方百计地希望跻身成收割者，反而对基础科学的付出冷潮热讽，那么这一文明的没落将无可避免。

那么在未来，人类社会是否能够演化得足够公正，将基于人性弱点聚敛的不义之财重新分配，用于激发人性的优点。例如将基于自私贪婪收割的智商税，用于探索自然更为深邃广袤的奥秘，我们只能寄望于人类文明自身的自省和睿智。

在《三体》中，由于人性中的弱点，主动放弃了威慑系统，任由“智子”驱逐而杀戮。作为报复，人类在外太空幸存的两艘战舰向宇宙广播了三体星的坐标，三体文明被光粒打击而毁灭。人类文明的毁灭指日可待，可惜人类再度错失了发展曲率驱动引擎的良机，这是人类逃离被覆灭的最后手段。歌者文明随手向太阳系扔出了“二向箔”，太阳系的三维空间被二维化，人类文明在降维攻击中灭亡。