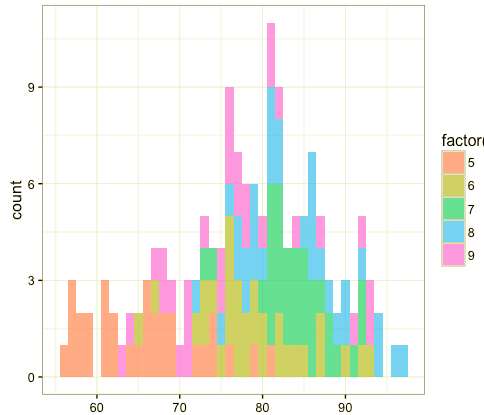如何可视化数据分布

作者：Marc Laforet

编译：weakish

编者按：Towards Data Science作者Marc Laforet，目前在Cyclica从事展示海量科学数据的web应用的全栈开发，简明扼要地分享了在数据分布可视化方面的经验。

来源：xkcd.com/539/

译文：

图一 光头：“我不是你的男朋友！”短发：“你当然是！”光头：“我不定期地和一些人约会。”

图二 短发：“但是，与任何约会对象相比，你和我呆在一起的时间在两倍以上。我是一个明显的异常值。”

图三 光头：“你的数学无可辩驳。”短发：“面对现实吧——我是你统计学上显著的他人。”（译者注：原文用了双关，“statistically significant”和“significant other”均为固定搭配，前者指统计学上具有显著意义，后者指配偶或恋人。）

将一切所需的数据处理成干净格式，很好地进行了时髦的统计分析之后，到了分析结果的时候了。这是可视化数据能帮上忙的地方。富含信息的数据可视化可以揭示新颖的洞见（也许你正和某人约会而没有意识到这一点），而当你需要向老板/客户传达发现时，它是无价之宝。

这篇文章将专门讨论一个我反复面对的可视化任务。在多年的数据分析生涯中，我常常发现自己想要比较多个数值数据分布。取决于分布的不同程度，再加上大量的分布的可能表示方法，这可能是一项需要技巧性的任务。通常，我比较分布的目标，要么是突出显示两者异常值之间的差异，要么是（更微妙的）两者分布之间的差异。说不定我想展示基于截然不同的标准收集的数据在同一统计过程下的表现会如何不同，或者应用一个统计学修正如何提升评分功能。

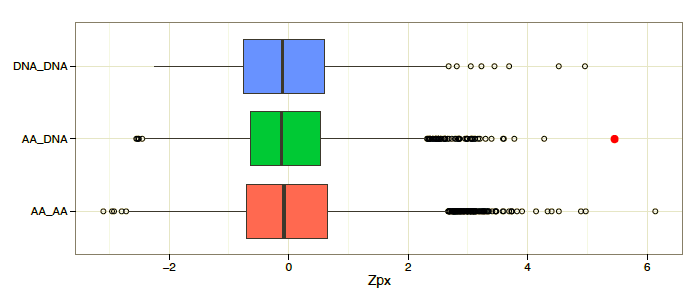
当我对比较异常值有兴趣时，我一般偏爱使用箱形图。箱形图在展示数据的总体分布的同时为异常值绘制了数据点。这些实实在在的数据点使得异常值很容易辨识和比较。

让我们忽略这些数据实际上代表什么，因为那不重要。你可以看到，这些分布基本上差不多，而异常值很容易比较。红色（品红）分布具有最极端的异常值，其次是绿色分布的异常值（红色数据点）。对这一分析而言，红色分布是在之前计算得出的，我观测到了极端异常值，并且可以重现数据。而红色数据点，则是一个新发现。

如果你仔细查看了横轴，并且懂一点统计学的话，你也许会意识到我对数据集应用了一种统计学转换以放大分布离散值的差异。我将数值分布转换为z值。z值转换数据点，将和样本均值的差异基于标准差切分。

我一般首先用直方图可视化分布。你可以看到，上图中，直方图是一种糟糕的、不提供信息的查看数据的方式。不同组之间的样本数目的差异让我们无法通过直方图比较不同组的分布。在这里例子中，这一问题极端化到了看不见蓝色分布的程度。这一可视化方法同样不能比较异常值（事实上我们甚至看不到异常值）。基于以上可视化，我能得出的唯一结论是红色分布和绿色分布的均值差不多。

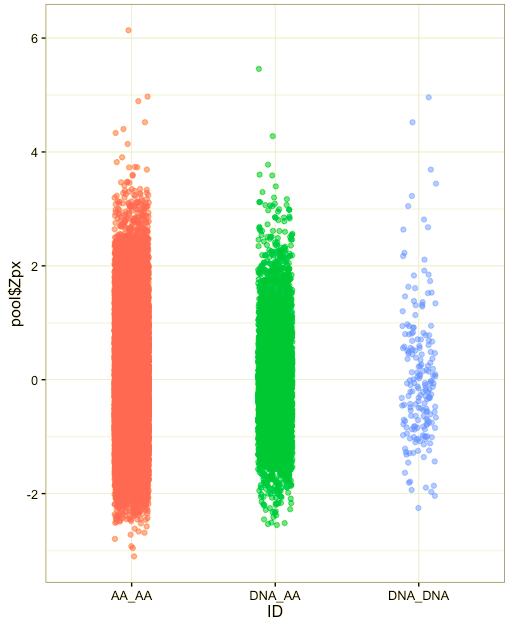
尽管我认为，在这个案例中，箱形图会是最佳的选项，但它们看起来非常正式，人们常常不知道如何恰当地解读它们（四分位距，分布，这都什么呀？）。此外，箱形图没有给出创建它们的样本尺寸的洞见。对于缺乏统计学知识的受众而言，strip plot可能更加直观，因为他们能看到所有的数据点。strip plot也给出了关于分布的样本尺寸的洞见。我喜欢给数据点加上一点抖动和透明度，让这些图形看起来更漂亮。

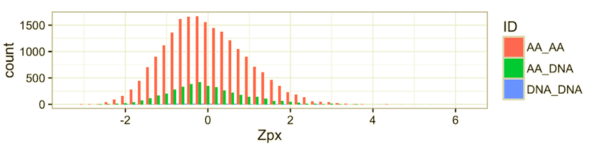
让我们进入第二部分，比较分布的不同。如果要比较的分布具备相同的样本尺寸，而且比较的分布数量不超过3个，那么直方图是一个很好的选项。如果用直方图比较很多个分布，那么你将得到一个非常繁忙的图形，使你难以看清数据。

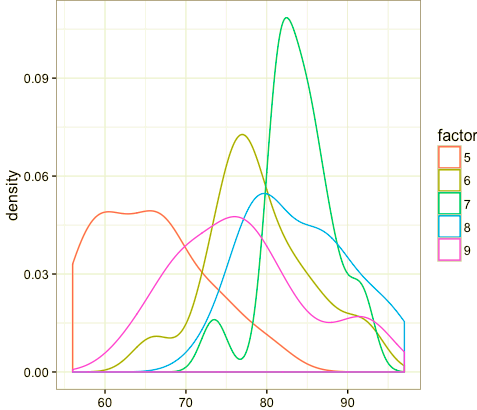
在没有什么特别好的选择的前提下，我比较倾向于使用核密度图。它不是那么漂亮但你确实可以查看和比较分布。为了克服核密度图的缺点，我在最近的一个项目中使用了一种直方图的变体，step plot，效果非常好。如果你的图形变得难以查看，我会建议你改变下表示数据的方式。

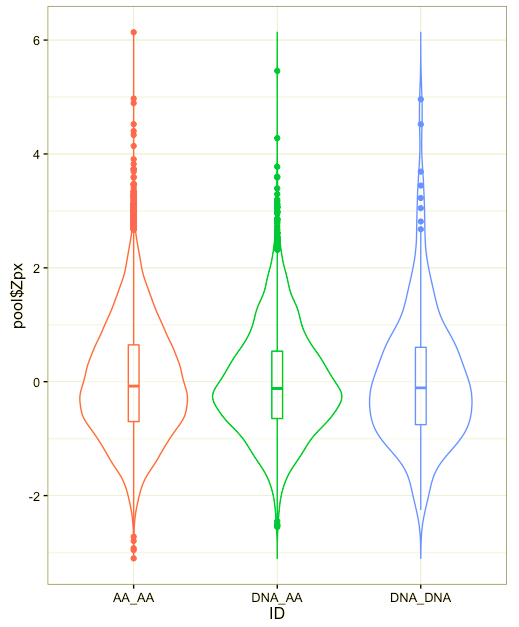
如果你都想要？在这种情况下我会使用提琴形图。我发现提琴形图变得越来越流行了，而提琴形图的一些变种让它们更加强大。提琴形图基本上是箱形图配上旋转的核密度图。下图中，我在旋转核密度图的内部绘制了箱形图。

好了，目前就这些。我使用R的ggplot2包绘制了文中所有的图形。有时我也用python的matplotlib和seaborn画一些图。第二个案例中的数据集来自R自带的空气质量数据集，其他数据集来自我的硕士论文。

本文相关代码可以通过GitHub获取（mlafore3/visualizing_distributions）。如果你愿意，欢迎添加更多图形。如果你认为有更好的分析数据的方式，欢迎留言告知。

原文地址：https://towardsdatascience.com/how-to-visualize-distributions-2cf2243c7b8e