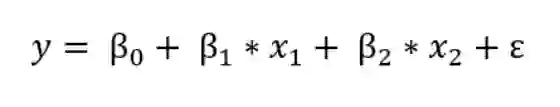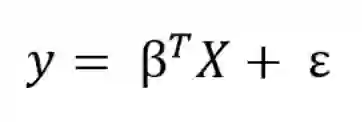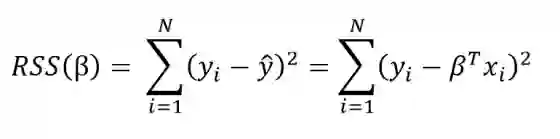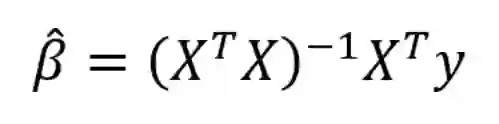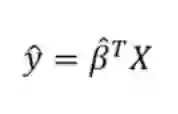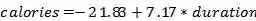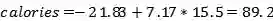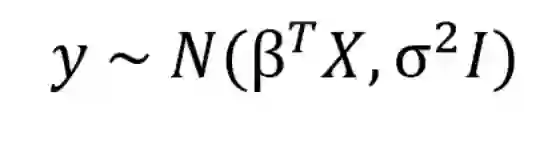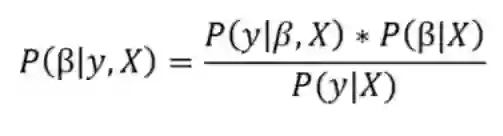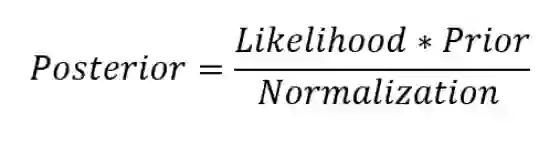【干货】贝叶斯线性回归简介（附完整代码）

会员服务 ·

【干货】贝叶斯线性回归简介（附完整代码）

2018 年 4 月 24 日 专知

【导读】应用贝叶斯推理的重点领域之一是贝叶斯线性模型。我们首先简要回顾一下频率主义学派的线性回归方法，接着介绍贝叶斯推断，并试着应用于简单的数据集。

作者 | William Koehrsen

编译 | 专知

参与 | Yingying, Xiaowen

Introduction to Bayesian Linear Regression

频率主义线性回归概述

线性回归的频率主义观点可能你已经学过了：该模型假定因变量（y）是权重乘以一组自变量（x）的线性组合。完整的公式还包含一个误差项以解释随机采样噪声。如有两个自变量时，方程为：

模型中，y是因变量，β是权重（称为模型参数），x是自变量的值，ε是表示随机采样噪声的误差项或变量的影响。

线性回归是一个简单的模型，它可以很容易解释：是截距项，其他权重β表示增加自变量对因变量的影响。例如，如果是1.2，那么对于中的每个单位增加，响应将增加1.2。

我们可以使用矩阵方程将线性模型推广到任意数量的预测变量。在预测矩阵中添加一个常数项1以解释截距，我们可以将矩阵公式写为：

从训练数据中学习线性模型的目标是找到最能解释数据的系数β。在频率主义线性回归中，最好的解释是采用残差平方和（RSS）的系数β。 RSS是已知值（y）和预测模型输出之间的差值的总和（ŷ，表示估计的明显的y-hat）。残差平方和是模型参数的函数：

总和被用于训练集中的N个数据点。我们在这里不会详细讨论这个细节，但是这个方程对于模型参数β有封闭解，可以使误差最小化。这被称为β的最大似然估计，因为它是给定输入X和输出y的最可能的值。以矩阵形式表示的封闭形式解为：

（再一次，我们必须在β上放上'帽子'，因为它代表了模型参数的估计值。）不要让矩阵算术吓跑你！感谢像Python中的Scikit-learn这样的库，我们通常不需要手工计算（尽管编码线性回归是一种很好的做法）。这种通过最小化RSS来拟合模型参数的方法称为最小二乘法（OLS）。

我们从频率主义线性回归中得到的仅仅是基于训练数据的模型参数的单一估计。我们的模型完全被数据告知：在这个视图中，我们需要知道的模型的所有信息都编码在我们可用的训练数据中。

一旦我们有了β-hat，我们可以通过应用我们的模型方程来估计任何新数据点的输出值：

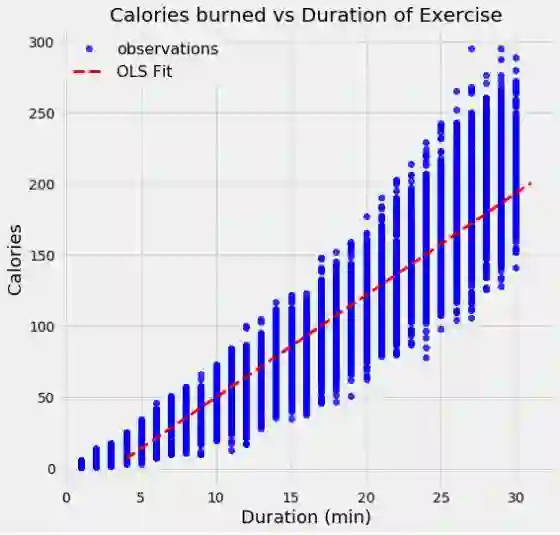
作为OLS的一个例子，我们可以对真实世界的数据进行线性回归，这些数据的持续时间和消耗的热量为15000次运动观察。以下是通过求解上述模型参数的矩阵方程得到的数据和OLS模型：

使用OLS，我们得到模型参数的单个估计值，在这种情况下，线的截距和斜率。我们可以写出由OLS产生的等式：

从斜坡上，我们可以说每一分钟的锻炼就能燃烧7.17卡路里。这种情况下的截距并不有用，因为它告诉我们，如果我们运动0分钟，我们会燃烧-21.86卡路里！这只是OLS拟合程序的一个人为因素，它找到了尽可能减少训练数据错误的线条，无论它是否物理上合理。

如果我们有一个新的数据点，说一个15.5分钟的运动持续时间，我们可以将其插入到方程式中，以获得燃烧卡路里的点估计值：

最小二乘法给出了输出的单点估计，我们可以将其解释为给定数据的最可能估计。但是，如果我们有一个小数据集，我们可能会将我们的估计值表示为可能值的分布，这就是贝叶斯线性回归。

完整代码：

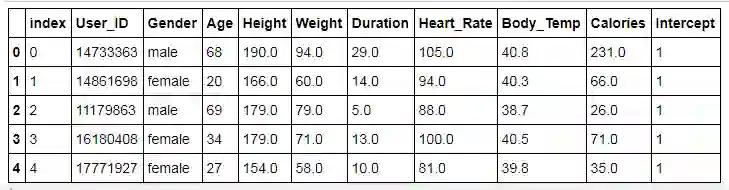
1. Load in Exercise Data

exercise = pd.read_csv('data/exercise.csv')
calories = pd.read_csv('data/calories.csv')
df = pd.merge(exercise, calories, on = 'User_ID')
df = df[df['Calories'] < 300]
df = df.reset_index()
df['Intercept'] = 1
df.head()

2. Plot Relationship


plt.figure(figsize=(8, 8))

plt.plot(df['Duration'], df['Calories'], 'bo');
plt.xlabel('Duration (min)', size = 18); plt.ylabel('Calories', 
size = 18); 
plt.title('Calories burned vs Duration of Exercise', size = 20);

# Create the features and response
X = df.loc[:, ['Intercept', 'Duration']]
y = df.ix[:, 'Calories']

3. Implement Ordinary Least Squares Linear Regression by Hand

# Takes a matrix of features (with intercept as first column) 
# and response vector and calculates linear regression coefficients
def linear_regression(X, y):
    # Equation for linear regression coefficients
    beta = np.matmul(np.matmul(np.linalg.inv(np.matmul(X.T, X)), X.T),
 y)
    return beta

# Run the by hand implementation
by_hand_coefs = linear_regression(X, y)
print('Intercept calculated by hand:', by_hand_coefs[0])
print('Slope calculated by hand: ', by_hand_coefs[1])

xs = np.linspace(4, 31, 1000)
ys = by_hand_coefs[0] + by_hand_coefs[1] * xs

plt.figure(figsize=(8, 8))
plt.plot(df['Duration'], df['Calories'], 'bo', label = 'observations', 
alpha = 0.8);
plt.xlabel('Duration (min)', size = 18); plt.ylabel('Calories', size = 18); 
plt.plot(xs, ys, 'r--', label = 'OLS Fit', linewidth = 3)
plt.legend(prop={'size': 16})
plt.title('Calories burned vs Duration of Exercise', size = 20);

贝叶斯线性回归

在贝叶斯观点中，我们使用概率分布而不是点估计来进行线性回归。 y不被估计为单个值，而是被假定为从正态分布中抽取。贝叶斯线性回归模型是：

输出y由一个以均值和方差为特征的正态（高斯）分布产生。线性回归的均值是权重矩阵乘以预测矩阵的转置。方差是标准差σ的平方（乘以恒等矩阵，因为这是模型的多维表达式）。

贝叶斯线性回归的目的不是找到模型参数的单一“最佳”值，而是确定模型参数的后验分布。不仅是由概率分布产生的响应，而且假定模型参数也来自分布。模型参数的后验概率取决于训练输入和输出：

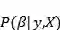
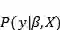
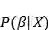
这里，是给定输入和输出的模型参数的后验概率分布。这等于输出乘以给定输入的β的先验概率并除以归一化常数的可能性。这是贝叶斯定理的一个简单表达式，贝叶斯定理是贝叶斯推理的基本基础：

让我们停下来思考这意味着什么。与OLS相比，模型参数有一个后验分布，它与数据乘以参数先验概率的可能性成正比。在这里我们可以观察到贝叶斯线性回归的两个主要好处。

1. 先验：如果我们有领域知识，或者猜测模型参数应该是什么，那么我们可以将它们包括在我们的模型中，这与频率方法不同，后者假设所有参数都来自数据。如果我们没有提前做出任何估计，那么我们可以使用非信息性的先验来确定正态分布等参数。

2. 后验：执行贝叶斯线性回归的结果是基于数据和先验的可能模型参数的分布。这使我们能够量化我们对模型的不确定性：如果数据少，后验分布将更加分散。

随着数据点数量的增加，可能性会冲刷先验，并且在无限数据的情况下，参数的输出会收敛到从OLS获得的值。

作为分布的模型参数的表达形式包含了贝叶斯的世界观：我们从最初的估计开始，即先验，并且随着我们收集更多的证据，我们的模型变得不那么错了。贝叶斯推理是我们直觉的自然延伸。通常，我们有一个最初的假设，当我们收集支持或反驳我们想法的数据时，我们改变了我们的世界模型（理想情况下这是我们的理由）！

实现贝叶斯线性回归

在实践中，评估模型参数的后验分布对于连续变量是难以处理的，所以我们使用抽样方法从后面抽取样本以近似后验。从分布中抽取随机样本以近似分布的技术是蒙特卡罗方法的一种应用。有许多用于蒙特卡罗采样的算法，其中最常见的是马尔可夫链蒙特卡洛变体。

贝叶斯线性建模应用

我将跳过本文的代码，但实现贝叶斯线性回归的基本过程是：为模型参数指定先验（我在本例中使用了正态分布），创建模型映射训练输入到训练输出，然后用马尔可夫链蒙特卡罗（MCMC）算法从后验分布中抽取样本作为模型参数。最终结果将是参数的后验分布。我们可以检查这些分布以了解发生了什么。

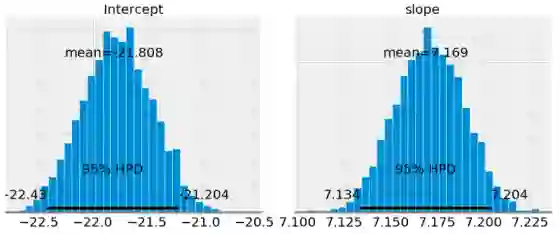
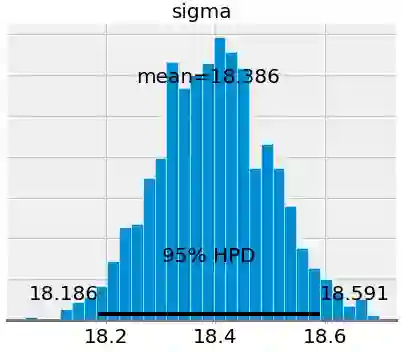
第一个图显示模型参数的后验分布的近似值。这些是MCMC 1000步的结果，这意味着算法从后验分布中抽取了1000步。

如果我们将斜率和截距的平均值与OLS得到的平均值进行比较（OLS的截距为-21.83，斜率为7.17），会发现它们非常相似。但是，尽管我们可以将均值用作单点估计，但我们也可以为模型参数提供一系列可能的值。随着数据点数量的增加，这个范围将缩小并收敛一个代表模型参数更大置信度的值。（在贝叶斯推断中，变量的范围称为可信区间，与频率推理中的置信区间的解释略有不同）。

当我们想用贝叶斯模型进行线性拟合时，我们可以绘制一系列线条，而不是仅显示估计值，每条线条表示模型参数的不同估计值。随着数据点数量的增加，线条开始重叠，因为模型参数中的不确定性逐渐减小。

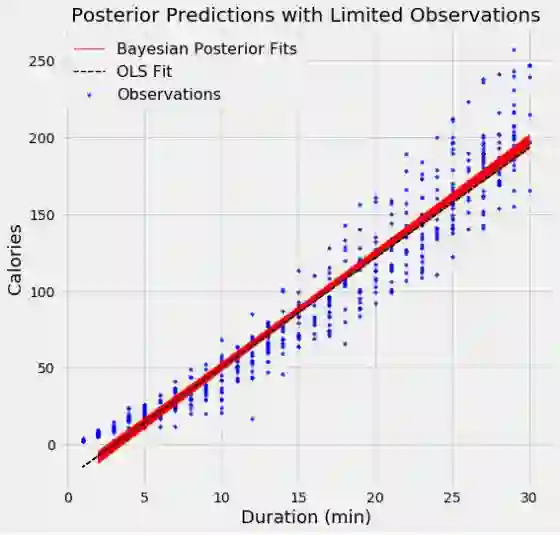
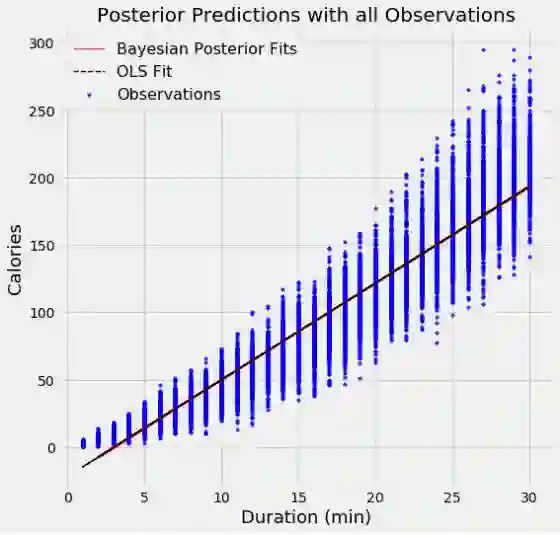
为了证明模型中数据点的数量的影响，我使用了两个模型，第一个模型，使用了500个数据点，第二个使用了15000个数据点。每个图表显示了100个从参数分布中抽样的模型。

当使用较少的数据点时，拟合中的变化更大，这表示模型中存在更大的不确定性。有了所有的数据点，OLS和贝叶斯拟合几乎完全相同，因为数据的可能性使得先验数据逐渐被覆盖。

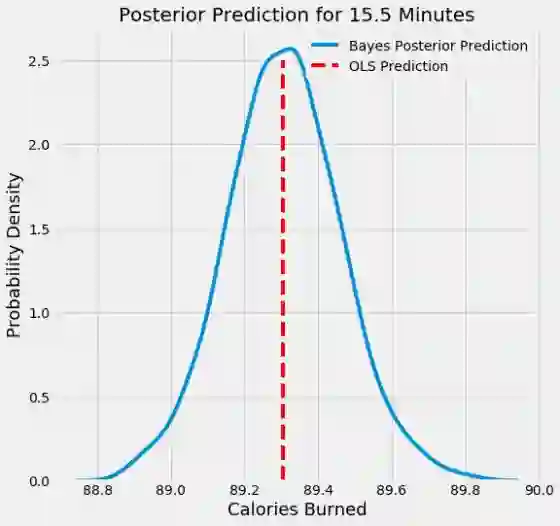
当使用我们的贝叶斯线性模型预测单个数据点的输出时，我们得到的仍是一个分布。以下是运行15.5分钟的卡路里数量的概率密度图。红色垂直线表示来自OLS的点估计。

结论

贝叶斯主义和频率主义的没有好坏，只有针对它们的合适的应用场景。

在数据有限或者我们想要在模型中使用某些先验知识的问题中，贝叶斯线性回归方法既可以包含先前的信息，也可以表明我们的不确定性。贝叶斯线性回归反映了贝叶斯框架：当我们收集更多数据时，可以改进对数据的估计。贝叶斯观点是一种直观的观察世界的方式，贝叶斯推理可以成为其频率主义者推论的有用替代方案。数据科学不是偏袒某一方，而是为了找出工作的最佳工具，并且使用更多的技巧才能使你更有效！

参考链接：

1.https://www.quantstart.com/articles/Bayesian-Linear-Regression-Models-with-PyMC3

2.http://twiecki.github.io/blog/2013/08/12/bayesian-glms-1/

3.https://wiseodd.github.io/techblog/2017/01/05/bayesian-regression/

4.PyMC3 Introduction

完整代码链接：

https://github.com/WillKoehrsen/Data-Analysis/blob/master/bayesian_lr/Bayesian%20Linear%20Regression%20Demonstration.ipynb

原文链接：

https://towardsdatascience.com/introduction-to-bayesian-linear-regression-e66e60791ea7

-END-

专 · 知

人工智能领域主题知识资料查看获取：【专知荟萃】人工智能领域26个主题知识资料全集（入门/进阶/论文/综述/视频/专家等）