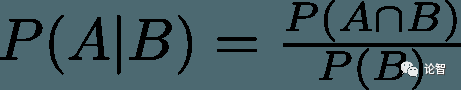零基础概率论入门：基本概念

2018 年 1 月 17 日 论智 weakish

来源：Toward Data Science

编译：weakish

编者按：概率论和线性代数是机器学习的两大基石。可是，砖头一样厚的概率论教材让许多人望而生畏。幸好数据科学家Jonny Brooks-Bartlett撰写了一系列零基础入门概率论的简明教程。让我们一起跟随Jonny探索概率的世界吧。

这么些年来，我读过很多关于概率论各个方面的文章，每篇文章看起来都需要不同级别的预备知识才能理解。我绝非这个领域的专家，但我觉得自己可以贡献一系列文章。我希望这些文章可以解释许多有关概率的概念。本文将是这个系列的第一篇，我将介绍一些基本定义。

定义和符号

通常概率至少和一个事件有关。这个事件可以是任何事。最简单的例子包括投骰和从口袋中抓取有颜色的球。在这些例子中，事件的结果是随机的（投骰时无法确定最终的点数），所以表示这些事件的结果的变量称为随机变量（常常缩写为RV）。

我们常常想知道一个随机变量取一个特定值的概率。例如，投掷一个均质的6面骰时，点数是3的概率是多少？“均质”一词很重要，因为它告诉我们骰子落地时6个面（1、2、3、4、5、6）朝上的概率是相等的。从直觉上，你也许会说答案是1/6。没错！但我们如何以数学的形式表达这个呢？好，首先我们需要了解这里的随机变量是与投骰相关的事件结果。通常，随机变量用大写字母表示，这里，我们用X表示。所以，我们想知道X=3的概率。但是数学家写东西的时候可懒了，“概率是多少？”简写为字母P。因此，“当我投一个均质的6面骰时，点数为3的概率是多少？”在数学上记作“P(X=3)”。

概率的3种类型

我们上面介绍了随机变量和概率的一些记法。然而，概率可能会变得非常复杂。也许首先需要理解的是概率有不同的类型。

边缘概率（Marginal Probability） 事件A的边缘概率为A发生的概率P(A)。例子：从一副扑克牌中抽出一张红色的牌的边缘概率是P(红) = 0.5

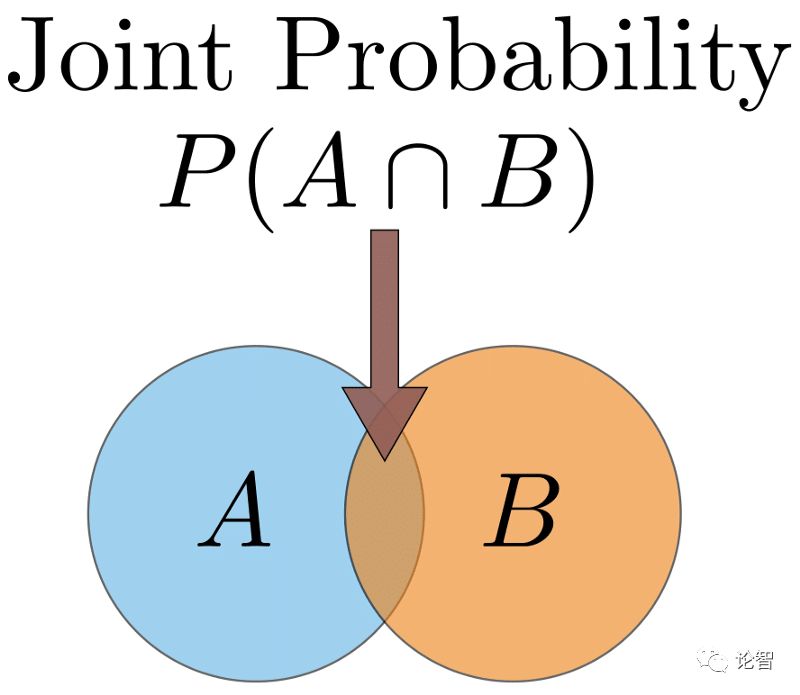
联合概率（Joint Probability） 两个以上事件的交集的概率。我们可以用文氏图（Venn Diagram）可视化这一概念，我们用两个圆代表两个事件，两个圆重叠的部分即为联合概率。（见下图）事件A和B的联合概率写作P(A ∩ B)。例子：从一副扑克牌中抽出一张红色的4的概率为P(红4) = 2/52 = 1/26。（一副扑克牌有52张牌，想抽到的是红心4和方块4）。后面我们会详细讨论这个例子。

条件概率（Conditional Probability） 条件概率是已知某（些）事件已经发生的前提下，另一（些）事件发生的概率。已知事件B已经发生时，事件A发生的条件概率写作P(A|B)。例子：已知我们抽到了一张红色的牌，这张牌是4的概率为P(4|红) = 2/26 = 1/13 （一副扑克牌有52张牌，26张红色的，26张黑色的。现在因为我们已经抽到了一张红色的牌，我们知道我们抽取的范围是26张牌，因此第一个除数是26）。

文氏图的重叠之处表示联合概率，也就是事件A和事件B同时发生的概率。如果事件之间没有重叠，那么联合概率将是零。

连接概率类型：乘法法则

乘法法则是一个连接所有3种概率类型的美丽等式：

例子的进一步解释

有时候联合概率和条件概率的区别相当令人困惑，所以让我们尝试用抽扑克牌的例子来理解两者的区别。

当我们想要知道抽到一张红色的4的扑克牌的概率（红色和4的联合概率）时，我想让你想象一下，把所有52张牌面朝下放置，然后随机选中一张。在这52张牌中，有2张是红色的，同时数字是4（红心4和方块4）。所以联合概率是2/52 = 1/26。

而当我们想要知道已知抽中的牌是红色的时候，抽中数字是4的牌的概率，即条件概率P(4|红)时，我想让你再想象一下有52张牌。不过，在随机抽取一张牌之前，你给所有扑克牌排了个序，选中了所有26张红色的牌。现在你把这26张牌面朝下放置，然后随机选择一张牌。同样，这些红色的牌中有两张数字为4，所以条件概率是2/26 = 1/13

如果你偏好数学，那我们也可以转而使用上面定义的乘法法则来计算联合概率。我们首先整理一下等式，让联合概率P(A ∩ B)成为等式的主题（换句话说，我们把P(A ∩ B) 放到等号的左边，把其他项都放到等号的右边）。重新整理后，我们得到P(A ∩ B) = P(A|B) ✕ P(B)。让我们设定事件A是牌的数字为4的事件，事件B是牌的颜色是红色的事件。如前所述，P(A|B) = 1/13，而P(B) = 1/2（一半的牌是红色的）。因此P(A ∩ B) = 1/13 ✕ 1/2 = 1/26。

概率法则：“和”与“或”

和

在联合概率中，我们已经遇到过“和”的情况，然而，我们并不知道如何计算“和”的概率。所以让我们来看一个例子。假设我们有两个事件：事件A——抛掷一枚均质的硬币，事件B——投掷一枚均质的骰子。我们也许会想知道骰子的点数是6而硬币正面朝上的概率。所以，为了计算骰子点数为6和硬币正面朝上的概率，我们可以把上面的乘法法则重新整理一下P(A ∩ B) = P(A|B) ✕ P(B)。我们知道事件A是丢硬币而事件B是扔骰子。因此P(A|B)意味着“当我们已经扔出一枚点数为6的骰子时，抛出一枚正面朝上的硬币的概率”是多少？”直觉告诉我们，丢硬币与扔骰子无关。这两个事件是独立（independent）事件。在这个场景下，不管骰子的点数是多少，丢硬币得到的结果都是一样的。数学上我们将其表达为P(A|B) = P(A)。因此，当事件相互独立时，联合概率为独立事件的边缘概率的乘积：P(A ∩ B) = P(A) ✕ P(B)。因此P(硬币正面朝上和骰子点数为6) = P(A=正面, B=6) = 1/2 x 1/6 = 1/12。

注意上面的P(A=正面, B=6)，事件之间的逗号是联合概率的简写。

值得注意的是，在现实世界的场景中，事件被假定为独立的（即使事实上并非如此）。这主要是因为，假定事件是独立的大大简化了数学。附带的好处是所得的结果通常很有用。在数据科学中，朴素贝叶斯可能是这方面最常见的例子。朴素贝叶斯通常能很好地处理文本分类问题。

或

在“和”法则中，我们将单独概率相乘。在“或”的场景下，我们需要将单独概率相加，然后减去交集。在数学上，我们将其写作P(A ∪ B) = P(A) + P(B) - P(A ∩ B)。你可能会问，为什么我们要这么做？好吧，让我们回顾一下上文中的文氏图。如果我们把A圆和B圆相加，那么其中的重叠部分算了两次。因此，我们需要减去交集。

所以，让我们把上面的例子改成寻找投出点数为6的骰子或扔出正面向上的硬币的概率。这是P(硬币正面向上或骰子点数为6) = P(A=正面 ∪ B=6) = 1/2 + 1/6 - 1/12 = 7/12

注意，我们使用并集符号∪表示“或”的场景。

有些情况下我们不必减去交集。如果文氏图中的两个圆没有重叠部分，那我们自然就不用减去交集了。当代表两个事件的圆没有重叠部分的时候，我们说这两个事件互斥（mutually exclusive）。这意味着两者的交集为零，在数学上写作P(A ∩ B) = 0。让我们看一个例子。假定我们想知道掷出点数为5或6的骰子的概率。这两个事件是互斥的，因为我们不可能同时掷出5点和6点。因此，它们在文氏图中的圆互不重叠。所以，掷出5点或6点的概率等于1/6 + 1/6 = 1/3 （我们没有减去任何东西）。