傅盛：不期望凡战皆胜，但务必追求胜的方法

在2017级混沌创业营第三模块“生物学思维与产品创新”的课堂上，傅盛展示了他的课后作业，分享了他啃了一个多月的书——《复杂》。

快40岁的年纪，还像小学生一样阅读、做作业，学习哲学、生物学、心理学这些硬知识，这就是傅盛在混沌创业营的生活。他说，这是因为，他真心觉得这些东西对创业有用，别无其他。

前几天，《财富》（中文版）公布了2017年“中国40位40岁以下的商界精英榜单”，傅盛连续第4年上榜。在这个属于学习型创业者的时代，我们越来越看到深度思考为商业创新赋予的力量。

2018年混沌创业营已经开始招生，期待与中国最具思考力的创业者同行（点此了解更多）。

文｜傅盛

  混沌创业营学员、猎豹移动联合创始人兼CEO

                

我一直认为，有些书属于开天眼的书。比如《商战》、《从0到1》、《软件创新之路：冲破高技术营造的牢笼》。正是这几本书，让我对战略和产品的理解，上了大台阶，受益至今。

 

而这一次，我要给大家推荐由梅拉妮·米歇尔著作的一本天书《复杂》。真的是烧脑，啃了一个多月。 

01

不废话，先说《复杂》第一部分精彩的前两章。

 

很长一段时间，我个人一直非常遵循牛顿世界观，认为所有事物都可准确预测，直到我遇到了这本书。它用昆虫系统和免疫系统开篇解释了“复杂系统”。

 

我们知道，单个蚂蚁没什么智能，甚至没什么视力，但整个蚁群却是一个高效运作的、难以解释的、集体智能的复杂系统。

同样，免疫系统也是单一细胞在没有中央控制的情况下一起高效工作。它们到处巡逻，并在遭遇入侵后，迅速摧毁入侵者，同时繁衍后代，产生抗体。以上，都不是被规划出来的复杂系统。

 

而牛顿世界观其实是一种“钟表宇宙”，可预测，可规划。数学家拉普拉斯认为，其中蕴含了如钟表般精准预测的观念。他曾在1814年断言，根据牛顿定律，只要知道宇宙中所有粒子的当前位置和速度，原则上就有可能预测任何时刻的情况。

 

相反，混沌系统则是一种“非线性系统”，不可预测。如果系统是混沌的，在测量初始位置时，即使只有极其微小误差，当预测其未来的运动时，也会产生巨大的误差。对于这样的系统，一点点误差，不管多小，也会导致长期预测不精确。

 

简言之，系统存在混沌。也就意味着，拉普拉斯式的完美预测，不仅实践中无法做到，原则上也是不可能的。

 

正如，我们永远也无法知道X小数点后的无穷多位数值。

 

这是一个非常深刻的负面结论。它与量子力学一起，摧毁了19世纪以来的乐观心态——认为牛顿式的宇宙，会像钟表一样沿着可预测的路径运行。

 

当然，看似混沌的行为，也有可能来自确定性系统。然而，一些简单的、确定性系统的长期变化，由于对初始条件的敏感依赖性，原则上却无法预测。

尽管混沌系统的具体变化，无法预测。可大量混沌系统的普适共性中，却有一些“混沌中的秩序”。例如，通往混沌的倍周期之路，以及费根鲍姆常数。

 

因此，细节上，预测变得不可能，但在更高的层面上，混沌系统却是可以预测的。所以，我的结论是——放弃确定性的直觉期待，用概率论的思维看待世界。

 

就这一点而言，原则就是坚决服从概率。

比如，我不会要求同事把每件事都做成，但我要求他们努力在每件事上追求更高的成功概率。不因小概率错几次，就动摇。没有一个人能在每件事上都做出正确的决定。胜利者，本质上只是能够坚定不移地去实践高概率的方向。

 

再说《复杂》第二章的热力学定律，即熵增定律。熵总是不断增加至最大，直至可能的最大值。除非通过外部做功，否则自身永远不会减少。

比如，冷的地方，越来越冷。如果你不加热，一杯水只会更冷。别的领域也一样。比如，你的房间只会越来越乱，除非你刻意收拾。

 

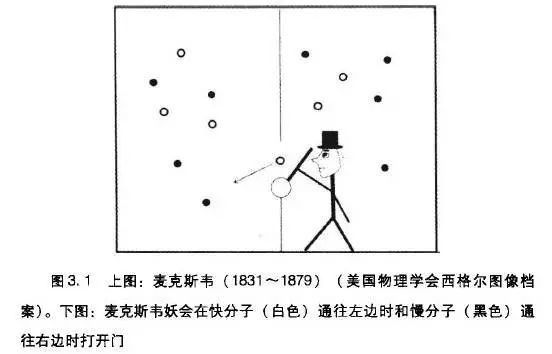
这时候，麦克斯韦提出了一个著名的思维实验——“麦克斯韦妖”来质疑熵增定律。

什么实验呢？

假设一个盒子里，有一扇不消耗任何能量的门在盒子中间，中间有一个小妖，如果看到快的分子，就把它放到门左边；如果看到慢的分子，就把它放在门的右边。

最后的结果就是：左边全是快分子，就会热；右边全是慢分子，就会冷。然而却没有做功，最终左边的熵，减少了。

 

为什么没做功，熵却减少了呢？这岂不是违反了热力学第二定律？

 

这个难题难住了当时所有天才。直到60年后，杰出的匈牙利物理学家Leo Szilard提出：小妖的“智能”，也就是获得信息的行为，其实做功了。而Szilard也是第一个将熵和信息联系起来的人。

 

这之前，全世界都认为人脑中想的东西和现实中分子运动之间，没有任何关联。而这个结论，第一次打通了信息学和热力学。

由此可见，许多看上去相距甚远的、不同的学科，微观层面完全迥异，但在大尺度上有着惊人的一致性。

只是有时候，我们过于埋头钻研自己的学科，而没能在一个更宏大的视角去看待这些学科。

这也是《复杂》这本书从诸多不同领域抽取不同例子想要提出的一个问题——所有的复杂系统有没有一个底层的统一规律？如果有，会是什么？

 

这也是接下来要讲的《复杂》第二部分——计算机中的生命和进化。

02

讨论之前，我们必须明确：生命的特征是什么？是自主？新陈代谢？自我复制？还是进化和适应？这些特征计算机可以实现吗？

 

《复杂》从遗传算法着手解答了这些问题。这部分内容，也是我觉得这本书最最最精彩的地方，甚至让我的写代码之魂，重新开始燃烧。

 

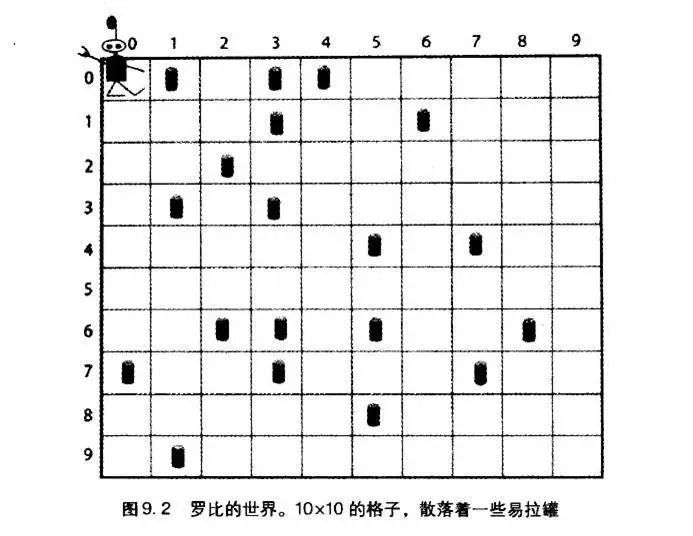
举个例子，清扫机器人罗比。它是一个可简单而详细阐述遗传算法思想的例子。

我们看到下图的罗比，身处一个10*10的二维世界，同时周边随机散布着待清扫的罐子。罗比只能看到五个方向（东南西北中），只能有七个动作（向东移动、向南移动、向西移动、向北移动、随机移动、不动和清扫罐子）。

移动并清扫一个罐子得10分，移动但没扫到罐子扣1分，撞墙扣5分，每次清扫，罗比会进行200个动作，这样总分会是500分。

我们用传统策略（有罐子就清扫，然后就往有罐子的方向上移动并清扫，否则就随机移动）测试10000次后，得到的平均分是346。

遗传算法采取的完全是另一套策略：它把每次编码看成一个生命体，由这些完全随机产生的生命体自己去完成动作，不定义策略好坏，彻底随机。

 

怎么生成初始群体呢？最简单的办法就是随机生产大量个体。

在这里，个体就是程序（字符串）。比如，初始群体有200个随机个体，这是策略之一。然后，计算当前群体中各个个体的适应度，选择一定数量适应度最高的个体作为下一代父母，将选出的父母进行配对，如此，再重复。

 

运行数代之后，比如得分比较高的A和B，注意比较高即可，我们就截取A的前半部分A1与B的后半部分B2，得到A1B2，再加上A2B1作为下一代，继续跑，同时设置一个很小的突变概率。

 

如此演化了1000代以后，我们得到了下面这张惊人的曲线。1000代的时候，平均得分是480几分（满分500）。我们发现，第1代非常差，只有负80几分，还不停撞墙。

但，就是这么一个起点非常差的清扫机器人罗比，通过拿出无数个体去观察，不断迭代之后，它甚至超出预料，产生了自己的策略——不是见地就扫，而是清扫完一片之后，再去清扫下一片。

图 遗传算法演化策略过程中，各代群体的最佳适应度（得分表现）

 

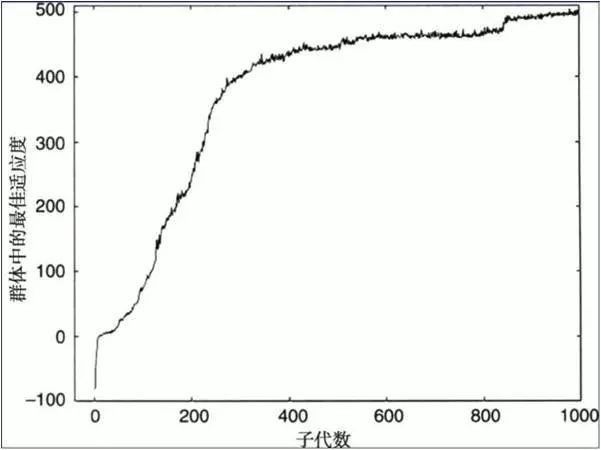
书中得出结论：显然，效率更高的策略，完全是自动进化来的，人类甚至都没能发现。这就是遗传算法。虽然运算量极大，但它自己完成了从简单的规则进化成为非常复杂的策略的过程。得到的结果，比人类精心打磨出来的策略，可能还要好。 

03

《复杂》的第三部分主要讲大写的计算，核心讲元胞自动机。

 

怎么理解呢？

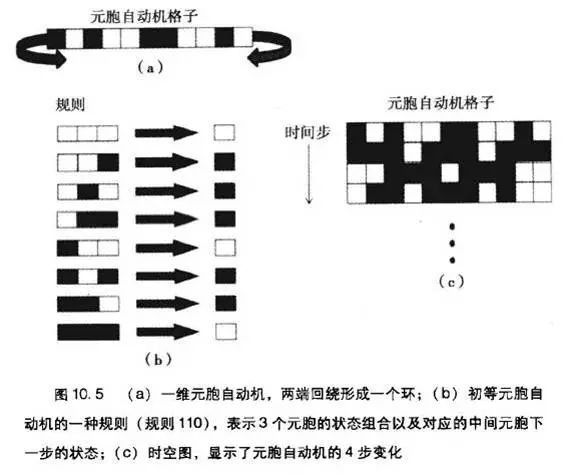
举个例子，你可以想象，有很多格子，每个格子根据周围的格子，决定自己亮还是不亮（见下图）。具体发光规则，可以自己制定。就这么简单的规则，随着时间序列一点点走下来，完成了极为复杂的演化，走出了一个极其复杂的图形。

这就是元胞自动机。由冯·诺依曼发明，他甚至证明过，元胞自动机等价于通用图灵机。他在通用计算机上很牛，但具有讽刺意味的是，这种结构被称为非冯·诺依曼结构。

 

同自然界的复杂系统一样，元胞自动机也是由大量简单个体（元胞）组成。不存在中央控制。每个个体都只与少量其他个体交互。元胞自动机也能表现出非常复杂的行为。它们的行为，很难甚至不可能通过其更新规则来预测。

 

这种极为简单的元胞自动机规则，究竟是如何产生出如此复杂的图样呢？沃尔夫勒姆曾说，这是他在科学中所遇到的最让人惊异的事物，并认为，这幅图包含了所有科学长久以来的一个谜团的线索——自然界的复杂性到底从何而来。

 

在他看来，自然界的很多东西，也能支持类似元胞自动机的通用计算，并跟《复杂》不约而同地提到了简单到不能再简单的蚂蚁和最终繁衍到全世界的蚁群，以及同样基于简单规则而产生强大计算能力的免疫系统。

04

说到这儿，大家可能也发现了，他们得出的结论其实就是——太多极为复杂的东西，在没有中央控制的环境下，由单个个体产生，最终表述出了非常复杂的行为。

 

所以，看完这本书，我有三个很切身的感悟：

 

第一个感悟，从世界可能都是运算构成的角度来看，我更加坚信人工智能的崛起是有宏大理论基础的。

 

第二个感悟，如果我们透过现象看本质，会发现所有这些所谓复杂系统的内在规律都是很相似的。包括公司和产品也一样。或许，具体演化中遇到的问题不同，各自总结的规律不尽相同，但这些东西背后的原因，可能产生的路径是有相关性的。本质相通。

 

第三个感悟，精准预测不可能，但概率依然存在。故而不期望凡战皆胜，但务必追求胜的方法。

 

还有一个非常重要的启发——就是自生长。公司或者产品本身，也是一个自生长的过程。有时，你觉得自己在控制产品，毋宁说，我们应该让产品更多去自生长。

 

读到遗传算法那部分时，我就在思考，公司应当如此——坚决进行一代一代的继承创新。每个人拿到产品时，就有自己的一个策略。你既能看到这个策略的成长性，当这个策略失效时，也要能快速生产下一代。

 

今天，我们思考问题的取胜办法，已经不该是一两个策略本身的成功，而是整个策略体系进化的成功。

 

与此同时，触类旁通的能力以及知识面宽广的重要性，更加值得强调。既然可能存在横跨复杂学科的统一规律，我们面对自己的问题时更应该学会从别的学科寻找灵感，且变得可能。

 

比如，我正在学习达尔文的进化论，思考人类的祖先怎么和恐龙竞争最后成功翻盘的知识，并由此思考猎豹怎样转型。

 

凡事皆有规律。各种复杂系统背后，统一大规律也许是有的。只有思考并认识到底层大规律，我们才有机会真正建立起“大思维格局”。

那么，我们读的各种书，吸收的各种知识，实践习得的各种经验，都能装得进去。而这本书的关键要领，也就在此。即扩展知识边界，尽可能接近简一律；触类旁通，必能大成。正所谓，大道至简。

*本文转载自微信公众号“ 盛盛GO”（ID：fstalk），转载请与原作者联系。

点击原文，了解更多招生信息