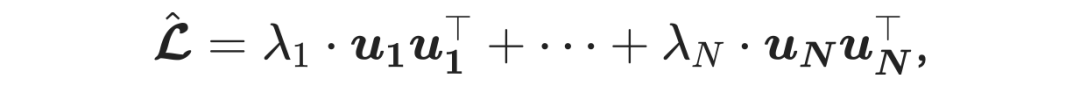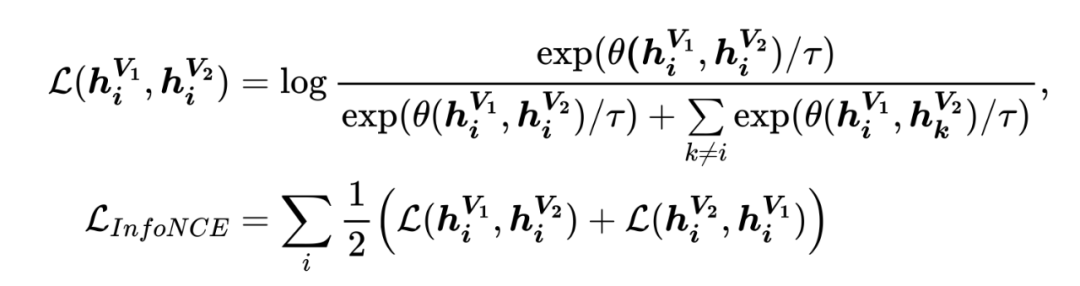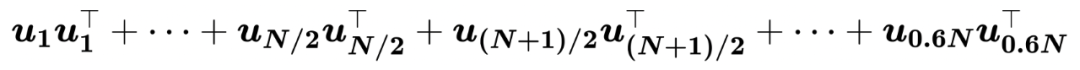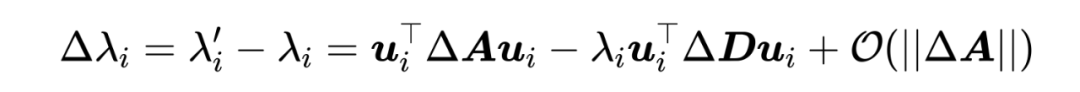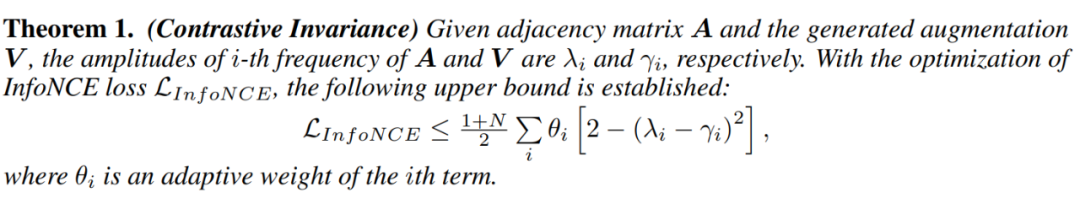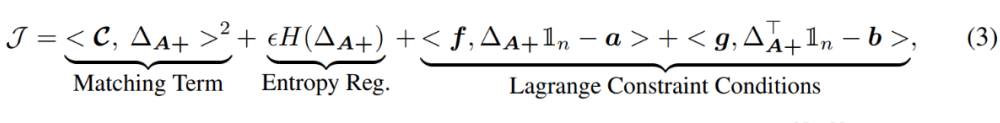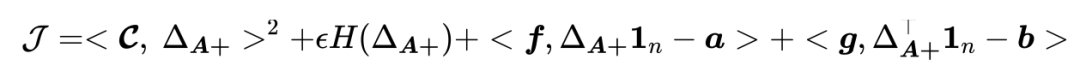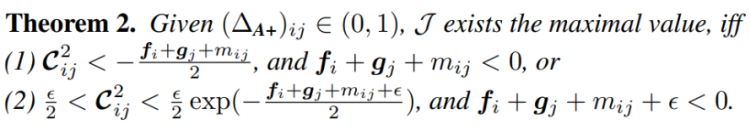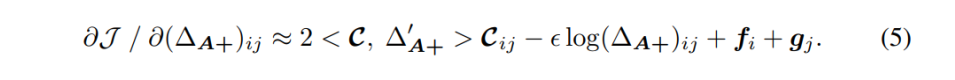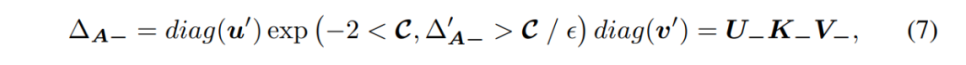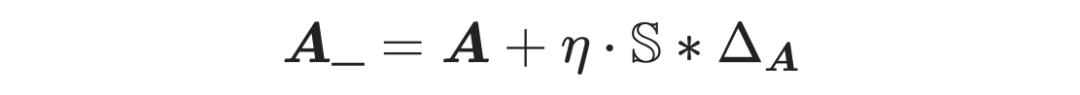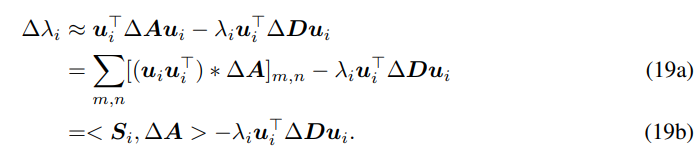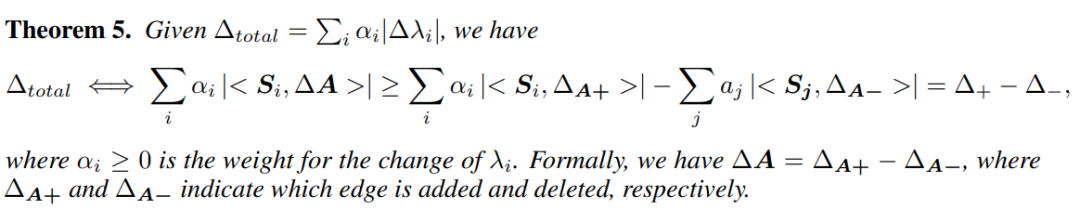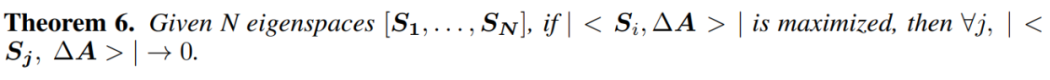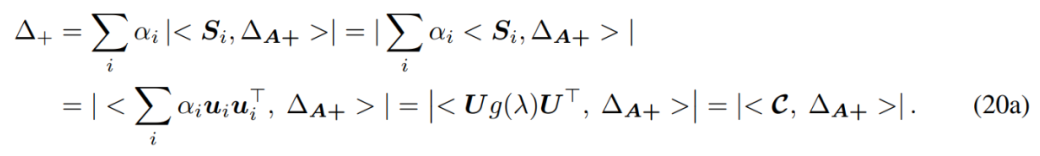会员服务 ·

NeurIPS 2022｜探明图对比学习的“游戏规则”：谱图理论视角

2022 年 10 月 14 日 PaperWeekly

©作者 | 刘念, 王啸

单位 | 北邮 GAMMA Lab

研究方向 | 图神经网络

论文标题：

Revisiting Graph Contrastive Learning from the Perspective of Graph Spectrum

收录会议：

NeurIPS 2022

论文链接：

https://arxiv.org/abs/2210.02330

代码链接：

https://github.com/BUPT-GAMMA/SpCo

近些年来，图对比学习技术（GCL）广受关注。然而在众多图对比学习技术的背后，一些开放的问题依然尚不清晰：图对比学习到底在表征里编码了什么信息？图对比学习技术为何是有效的？不同的图增广技术是否存在一般性的增广准则？这样的增广准则如若发现，又对我们理解和设计图对比学习算法带来怎样的启发？百川归海，道法同源，是时候需要对图对比学习技术进行重新审视并探寻其背后的“游戏规则”了。

简介

传统的图对比学习（GCL）框架如图 1（a）所示，其主要包括三个模块：图增广的设计、编码节点表示以及对比损失的选择。作为自监督学习的一种典型技术，GCL 旨在最大化不同图增广间的一致性，从而学得有效的不变表征。如今已经有许多图增广策略被提出，例如：启发式策略，包括随机删边/节点、特征掩码、利用扩散矩阵等；基于学习的策略，包括 Infomin、解耦、对抗训练等。尽管各式各样的图增广策略被提出，但是其背后的基本增广准则尚未被挖掘。

可以试想一下，在某些增广策略下，也许图结构发生了重大变化，原有对比学习中的正例也许就不再是正例了，原有的负例也可能不再是负例了。所以节点之所以增广后还是正例，之所以增广之后是负例，一定由于增广改变了某些信息而又保留了某些信息。那么边界在哪儿呢？由此引发了一系列的思考：

在增广图中，什么信息应该被保留或抛弃？
不同图增广策略的背后是否有一般性的准则？
如何去利用这样的准则来验证并提升现有 GCL 模型？

进一步思考图对比学习中的增广策略，表面上看都是改变了图结构，但我们知道，图结构的改变本质上往往意味着图谱上不同频率的强度发生变化，比如低频信息或者高频信息发生改变。这种想法启发了我们或许可以从谱域视角去探索图结构增广的有效性。

在本文中，我们首先通过实验去理解低频与高频信息在 GCL 中的作用，并从中归纳出了一般性的图增广准则（即 GAME rule ）；然后，我们提出 对比不变性理论 ，首次指明了 GCL 能够捕捉两对比图间的不变信息，从理论层面解释了 GAME rule 的有效性。该 GAME rule 开启了一种“第三方视角”可以审视主流图增广策略的优劣性，即通过看哪种增广策略更符合该 GAME rule，则哪种增广策略更适合图对比学习，因此也会更有效。

最后，我们将服从 GAME rule 的两个增广称为 最优对比对 （即 Optimal contrastive pair），并提出了谱图对比学习框架（ SpCo ）来实现最优对比对，这是一个通用性的插件，可提升已知 GCL 模型的效果。

预备知识

图定义为，其中是节点集合，是边集合。图的拉普拉斯矩阵定义为，其中是邻接矩阵，是相应的度矩阵。对称归一化拉普拉斯矩阵为，其中、分别是加了自环的邻接矩阵和度矩阵。

将进行特征值分解可得到，其中和分别是特征值和特征向量。假设，其中代表低频分量的幅值，表示高频分量的幅值，而图谱就定义为不同部分频率分量的幅值，记为，表示着哪部分的频率被加强或是被削弱。据此，我们可以写出

其中被定义为是第个频率的特征空间，记为。

图对比学习中常用的损失函数是 InfoNCE 损失 [1]，公式如下：

其中，和表示节点在增广和下得到的节点表示，是相似性度量函数，是温度系数。

图增广的影响：实验性探究

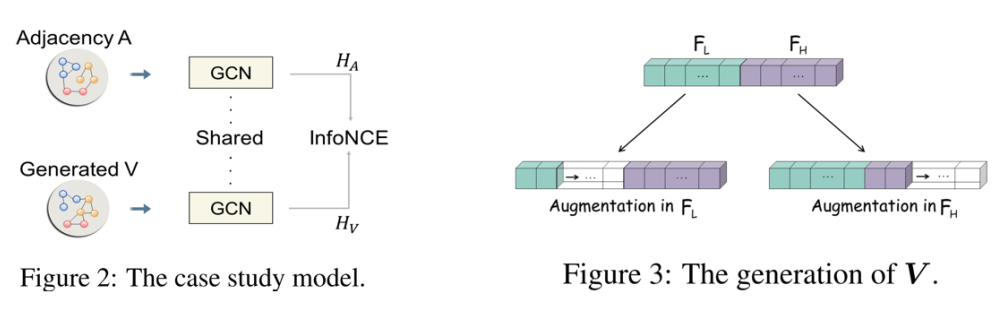
我们首先设计一个简单的 GCL 框架（如图 2），去探索在两个对比增广中，什么信息应该被保留：

在该框架中，我们对比邻接矩阵和生成的增广，利用共享的 GCN 对它们进行编码得到节点表示和，并利用 InfoNCE 损失训练整体框架。为了分析不同频率信息对于 GCL 的影响，我们从原始图中分别抽取和中不同频率的特征空间来构建（如图 3），表示分别对低频和高频信息以不同的强度进行增广。

以在中增广为例，首先保留所有的高频部分，在此基础上分别以 [20%, 40%, 60%, 80%] 的比例将中的特征空间按照从低频到高频的顺序加回。也就是说，在中增广 20% 得到的可表示为：

同理，在中增广 20% 得到的可表示为：

请注意，生成的的图谱，这是因为我们只想研究不同的效果，从而避免特征值带来的影响 [2] 。

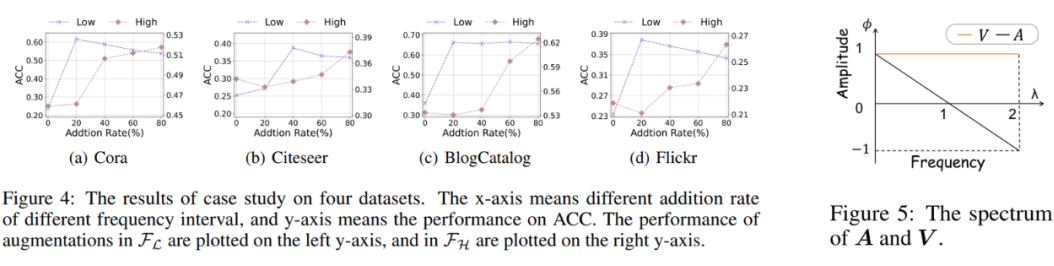
我们分别在 Cora，Citeseer，BlogCatalog，Flickr 数据集上做了实验，如图4所示。其中，横轴表示在不同频段内添加特征空间的比例，纵轴分别表示对低频/高频增广后的准确率。实验结果如下：

1. 当中最低频的信息被保留，效果达到最佳（紫线）

2. 当中加入更多高频信息时，效果逐步提升（棕线）

结合图 5 中给出的和的图谱，我们可以分析出如下结论：

1. 当中最低频的信息被保留，和间部分的频谱差异减小

2. 当中加入更多高频信息时，和间部分的频谱差异增大

将结果和分析相结合，我们提出了如下一般性的图增广准则，简称 GAME rule：

该准则表示：两个对比图增广的图谱间高频部分的差异应该大于低频部分的差异。我们将符合 GAME rule 的两个对比图增广称为最优对比对。

GAME rule分析

本节我们旨在进一步分析 GAME rule 的正确性，即满足 GAME rule 的两个增广是否能够提升下游任务的效果。

4.1 实验分析

我们将图 2 中的替换成 9 个当前主流的图增广，分别是 MVGRL [3] 的 {PPR matrix, heat diffusion matrix, pair-wise distance matrix}、GCA [4] 根据 {Degree, Eigenvector, PageRank} 随机删边以及 GraphCL [5] 的 {node dropping, edge perturbation, subgraph sampling}。首先利用特征值扰动公式来计算经过这 9 种增广后的特征值的改变：

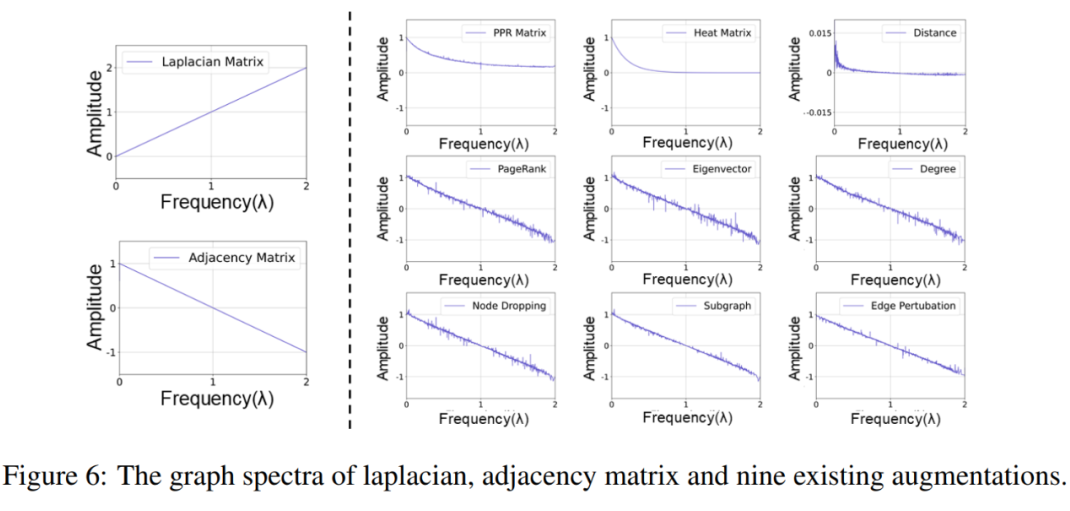
其中，是增广之后的结果，表示增广前后连边情况的改变。我们对 Cora 数据集施加这 9 种增广，并在图 6 中画出了增广后的图谱：

通过对比图 6 中虚线右边的曲线与左下角的曲线可以看出，，MVGRL 提出的三种增广（第一行）更好地符合 GAME rule 的要求，即它们和间的部分差异小，部分的差异大。因此我们有理由预测 MVGRL 的三种增广可能会取得更好的效果。

通过实验测试，可以在表 1 中看到，结果的确符合预期。很多启发式的策略各有其特点，而 GAME rule 在某种程度上提供了一种可供参考的指导意见，揭示了众多策略之中遵循一种基本规律。

4.2 理论分析

我们提出如下的对比不变性定理来描述 GCL 的学习过程：

其中，是一个和 GCN 参数相关的参数。在该定理中，我们找到了 InfoNCE 损失的上界。随着和对比的进行，InfoNCE 增大，右侧的上界也随之被抬高。为了达到抬高上界的目的，大的必将赋予在较小的一项上，而意味着和在第个频率分量上表现出了不变性。

至此，GCL 会学习到表征的不变性也给出了定理上的证明。请注意，如果两个对比图增广满足 GAME rule 准则，则它们频谱的低频部分差异会小于高频部分，再根据对比不变性定理，可得知这两个增广的共性低频部分将会被模型着重捕捉。而低频信息往往是对结果更有益的，因此我们从理论上证明了 GAME rule 的正确性。

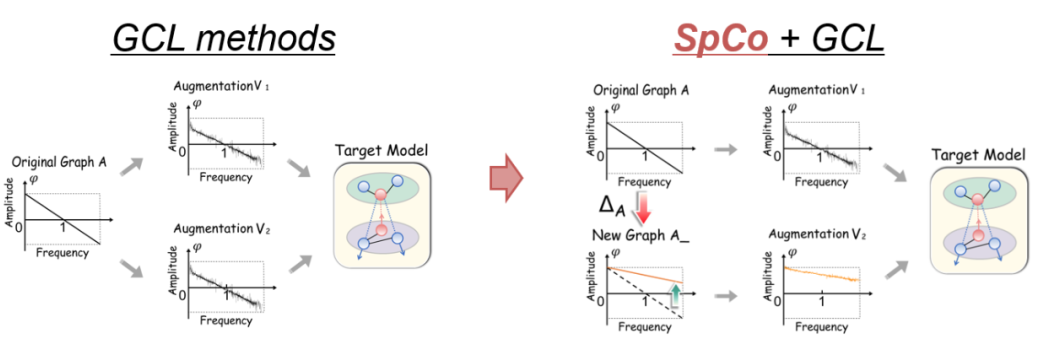
SpCo: 谱图对比学习

基于 GAME rule，我们想构建出一个最优对比对，从而提升现有 GCL 方法的性能。上图左侧是现有 GCL 方法的流程，以及每一步图增广的图谱。可以看出，由于增广和是从同一个得到的，因此很难成为最优对比对（除了像 MVGRL 那种特殊设计的）。为了实现我们的目标，我们从源头出发，先学得一个从到的变换，使得和形成最优对比对。继而再经过其他 GCL 提出的增广得到的和也将是最优对比对了（如上图右侧）。

那么，现在的问题是如何得到这样的？我们首先分解，其中和分别代表了边的增加和减少情况，它们的学习过程类似。根据理论推导（附文章结尾），我们首先给出了的优化目标（需被最大化）：

该目标由三部分构成：（1）匹配项（Matching Term），。为了最大化这一项，需要学着去“匹配” 。因此，直接决定着将会学成什么样子。那么如何来确定呢呢？在推导中，我们定义，其中是特征值的某种函数。

那么又如何来确定的形式呢？我们设，描述了和在频率上频谱的差异。根据 GAME rule，，，。进一步严格该条件，即我们要求是一个单增函数，随着的增大而增大。

由于来指导去体现出和间图谱差异随着频率的升高而增大（也就是的单增性）这一需求，我们自然地也将中的设为关于的单增函数。更进一步，我们发现拉普拉斯矩阵的频谱恰好也是关于的单增函数（见图6），因此，我们设，其中会随着训练的进行适当调整；

(2) 熵正则（Entropy Regularization）其中，

[6] ，是该项的权重。这项的作用是增加的不确定度，使得模型不只是关注于中特定的一些边，而让更多的边参与到优化过程中；

(3) 拉格朗日约束条件 （Lagrange Constraint Conditions）其中，和是拉格朗日乘子，和是预先定义的两个分布（文中均采用节点度分布）。这一项的作用是限制的行和和列和，防止学到没有意义的解。

接下来就是求解目标（3），首先求对的偏导：

在（4b）中，我们把从中提出来，将剩下的部分设为。在下面的定理中，我们给出了能取到极值的条件：

正常地，我们应该让（4b）等于 0，来精确解出该极值。然而，（4b）中同时存在对数函数和线性函数，是个超越方程，因此没有解析解。因此，我们转而让（4a）等于 0。考虑到随着训练的进行，学的会趋于稳定，因此重写（4a）如下：

和（4a）相比，我们仅仅将约等号右侧第一项中的替换成了，是上一轮训练得到的，并认为在本轮保持不变。因此，公式（5）等于 0 的解如下：

其中，

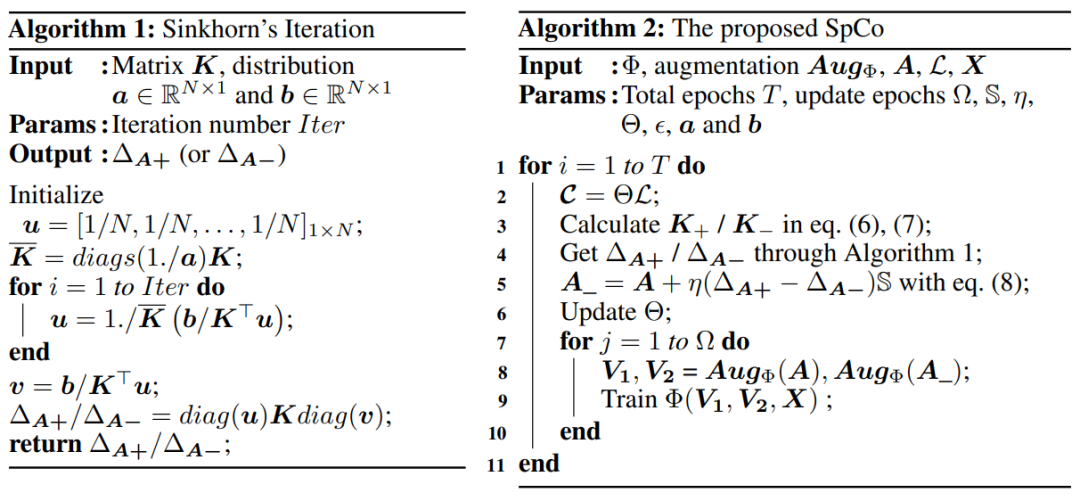
此时，由于和未知，和也尚未确定。为了计算和，我们重新利用公式（3）中的拉格朗日约束条件：以及。将这两个等式建模成 matrix scaling 问题 [7] ，并利用 Sinkhorn's Iteration [8] 进行求解（算法1）。下面定理指出了和间的差别上界：

最开始提到过，的计算过程和类似，其结果如下：

最后，我们结合公式（6）（7）得到了。利用学到的我们就能得到新的图增广：

其中 “*” 表示了两个矩阵的 element-wise 乘积，是组合系数。为了让稀疏化，我们利用范围矩阵来限制我们关注的范围，例如我们只关注一跳邻居的拓扑改变。整体流程如算法 2 所示。

实验

我们将基线模型中的 GCL 方法根据 loss 分为三类：BCE loss（DGI, MVGRL）、InfoNCE loss（GRACE, GCA, GraphCL）以及 CCA loss（CCA-SSG）。从这三类方法中分别选出一个（DGI, GRACE, CCA-SSG）与 SpCo 相结合，以此来验证插件 SpCo 的有效性和通用性，结果如表 2 所示。

可以看到和 base model 相比，结合上 SpCo 都能带来一定的提升。我们进一步可视化了和、和的图谱，如图 8 所示。可以看到，我们通过插入，成功地使得和形成最优对比对，继而后续的和也满足了 GAME rule 定理，从而带来表2中效果的提升。

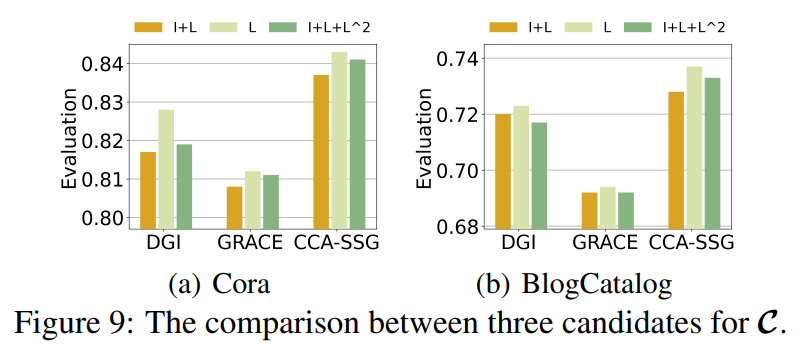
在上文中提到，我们设。然而，还有其他种选择来满足图谱单调递增的要求。在图 9 中我们在两个数据集上测试了三种可能的选择。

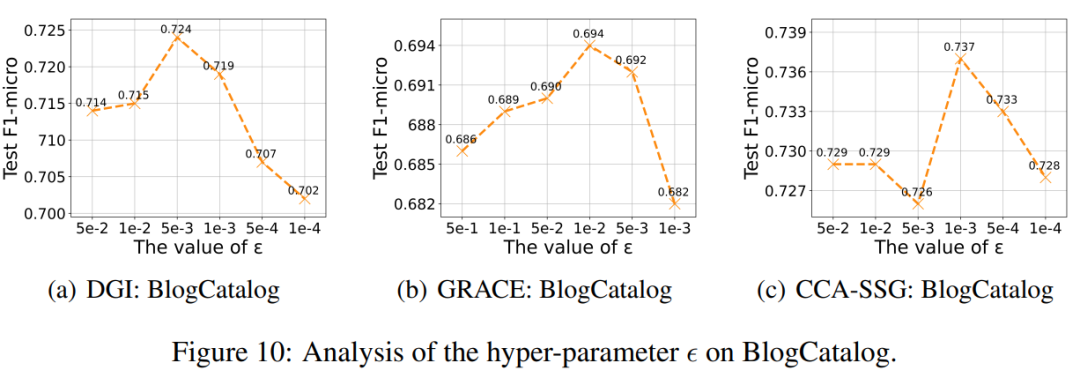
此外，我们还测试了公式（6）和（7）中涉及到的参数的敏感度，结果如图 10 所示：

更多实验，请参考原文。

推导： 的优化目标

该优化目标的推导基于特征值扰动公式（参考“实验验证2”部分），并忽略了高阶项：

我们用 ‘*’ 表示 element-wise 乘积，用表示中所有元素的和。上面的推导刻画了第个频率幅值的变化，我们将所有频率的幅值变化合在一起综合考虑，即可写成，其中控制着第个频率幅值变化的幅度。接着，有如下定理：

该定理给出了的下界，表明我们需同时最大化并最小化，从而最大化。我们主要讨论最大化部分，最小化的过程类似。最大化就是最大化，而下面定理告诉我们，只有某一部分的能得到最大化。

请回忆，GAME rule 要求部分的要大于部分的，因此根据公式（19b）应该学得和部分的特征空间产生关联（要大）。

如何做到这一点呢？我们可以将中部分的设的大于部分的，因此在最大化的时候，就会被诱导去与部分的产生关联。在此基础上，最大化可由下列推导实现：

在公式（20a）中，我们设，。由于要求部分的要大于部分的，因此我们可以把设为 单增函数 。由此可知，如果学着逼近某个预定义的，就可以实现最大化的目的。

如何确定 从图 6 中可以看到， 拉普拉斯矩阵 的图谱恰好满足单增的条件，因此我们设，其中是一个参数。

结合公式（20a），给出如下的优化目标：

其中每一项的具体含义正文中已经给出，这里不再赘述。

参考文献

[1] Aaron van den Oord, Yazhe Li, and Oriol Vinyals. Representation learning with contrastive predictive coding. arXiv preprint arXiv:1807.03748, 2018.

[2] Hoang Nt and Takanori Maehara. Revisiting graph neural networks: All we have is low-pass filters. arXiv preprint arXiv:1905.09550, 2019.

[3] Kaveh Hassani and Amir Hosein Khasahmadi. Contrastive multi-view representation learning on graphs. In ICML, pages 4116–4126, 2020.

[4] Yanqiao Zhu, Yichen Xu, Feng Yu, Qiang Liu, Shu Wu, and Liang Wang. Graph contrastive learning with adaptive augmentation. In WWW, pages 2069–2080, 2021.

[5] Yuning You, Tianlong Chen, Yongduo Sui, Ting Chen, Zhangyang Wang, and Yang Shen. Graph contrastive learning with augmentations. Advances in Neural Information Processing Systems, 33:5812–5823, 2020.

[6] Gabriel Peyré, Marco Cuturi, et al. Computational optimal transport. Center for Research in Economics and Statistics Working Papers, (2017-86), 2017.

[7] Arkadi Nemirovski and Uriel Rothblum. On complexity of matrix scaling. Linear Algebra and its Applications, 302:435–460, 1999.

[8] Richard Sinkhorn. A relationship between arbitrary positive matrices and doubly stochastic matrices. The annals of mathematical statistics, 35(2):876–879, 1964.

更多阅读