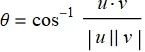[遇见数学] 继续图解高等数学系列, 下半部所用参考书籍为《托马斯微积分》第10版, 希望各位老师和朋友多提宝贵意见, 帮助我改进这个系列, 感谢关注!.
向量
9.1 平面向量
测量某些事物的大小, 如质量, 长度和时间, 只需要一个数和一个测量单位. 相关实数为标量.
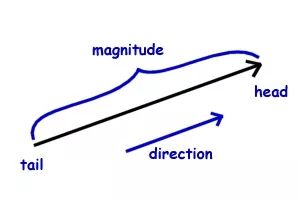
向量(vector, 或称矢量)是指一个同时具有大小和方向的几何对象, 可以用来描述力, 位移或速度.
![]()
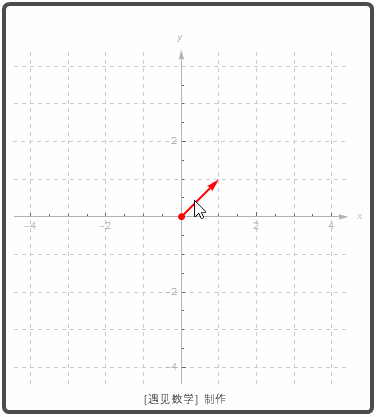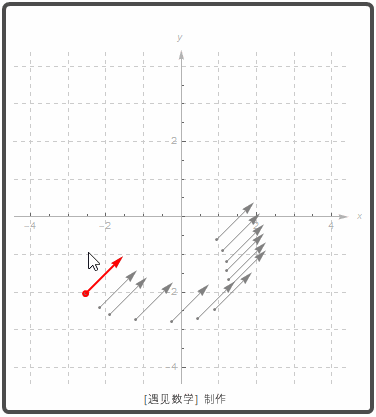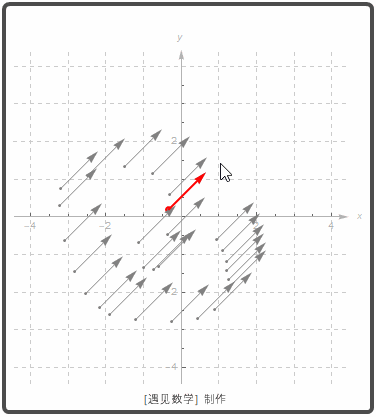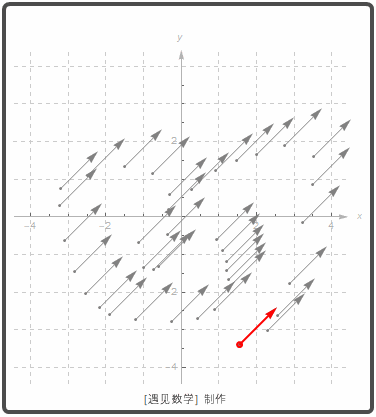
只要向量的大小和方向相同, 即视为相等的向量. 另外如果向量 v 的起点在原点, 则称之为是 v 的标准位置. 观察如下图所示在二维平面(Two-dimensional)下, 当移动一个向量, 所留下轨迹上都视为相同的向量:
![]()
向量的分量形式:如果平面上的一个向量 v 等于起点在原点 (0,0) 终点在 (v1
v
1
, v2
v
2
) 的向量, 则 v 的分量形式是 v=(v1,v2)
v=(
v
1
,
v
2
)
![]()
向量 v 的长度表示成 |v| 或 ||v||.
任何长度为 1 的向量 v 为单位向量. 如果 v=(v1,v2)
(
v
1
,
v
2
)
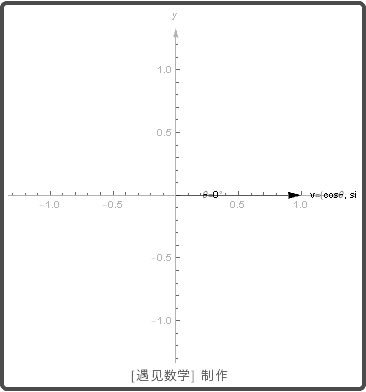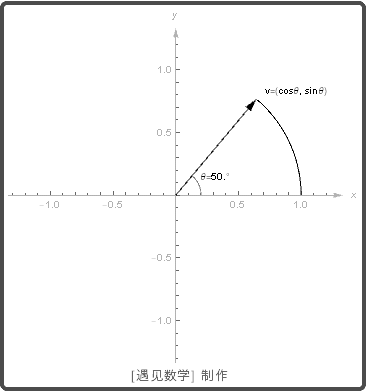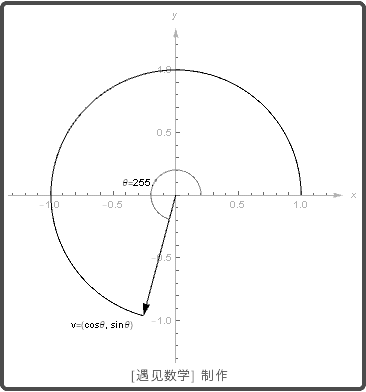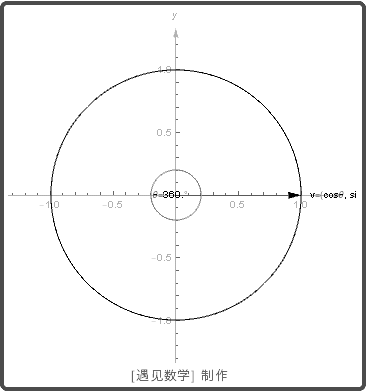
与正 x 轴成角 θ , 则 v=(cosθ, sinθ)
v=(cos
θ
, sin
θ
)
. 当 θ 从 0 到 2π 时, 单位向量取遍所有可能方向, 则绘制出单位圆.
![]()
向量的代数运算
设 u=(u1,u2)
u=(
u
1
,
u
2
)
和 v=(v1,v2)
v=(
v
1
,
v
2
)
是向量, k 是一个标量(实数).加法: u + v = (u1+v1, u2+v2)
u + v = (
u
1
+
v
1
,
u
2
+
v
2
)
数乘: k u = (k u1, k u2)
k u = (k
u
1
, k
u
2
)
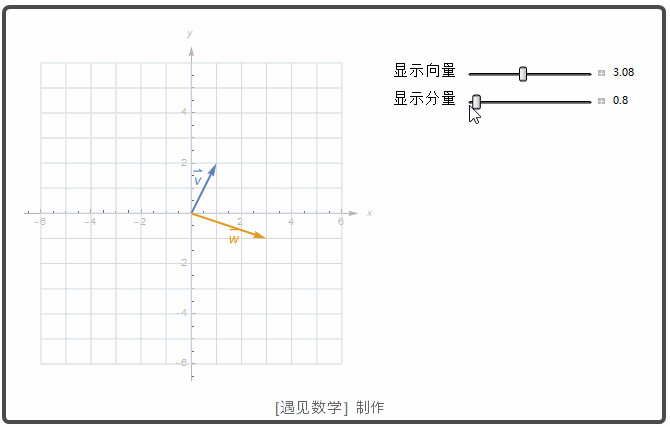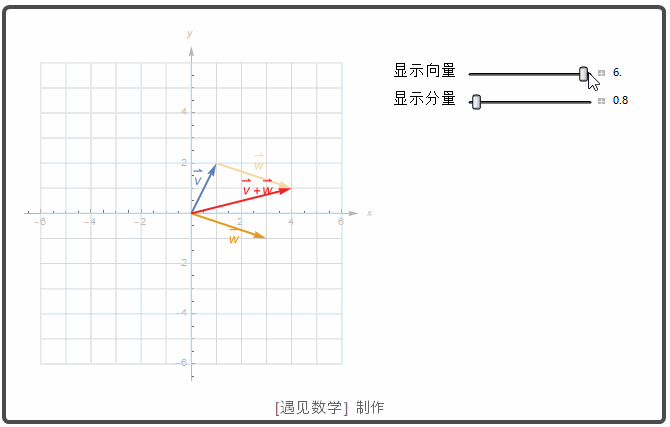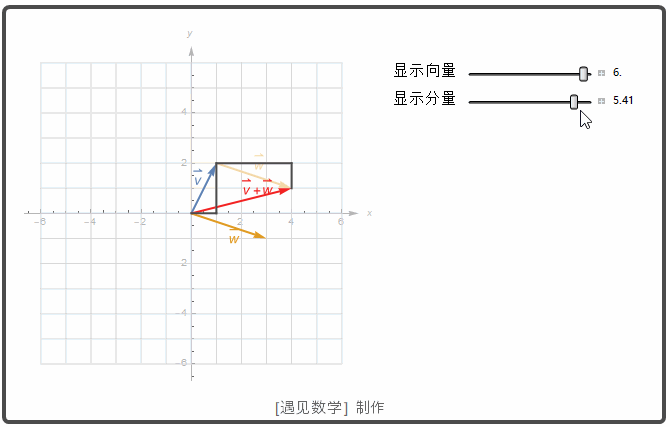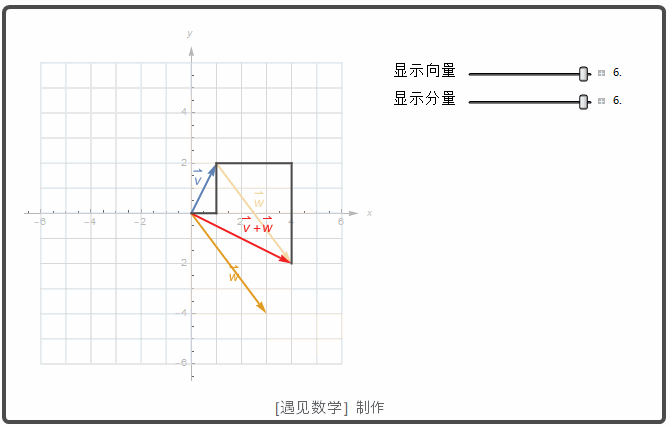
向量加法的定义几何解释如下动画, 图中一个向量的起点置于两一个向量的终点.
![]()
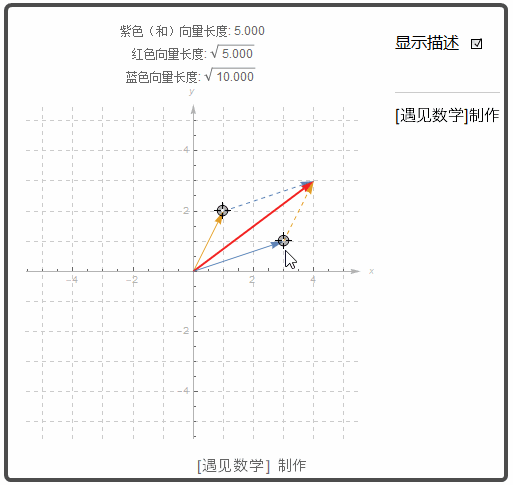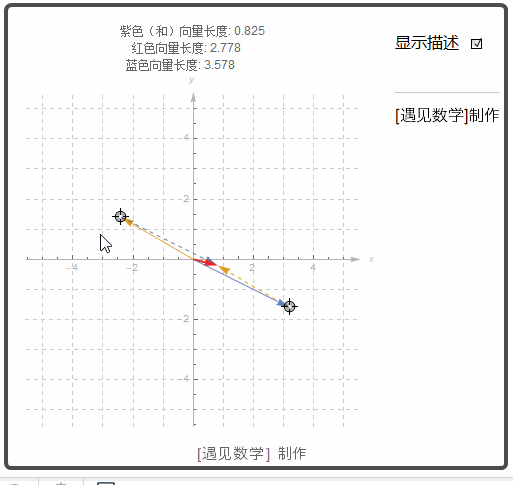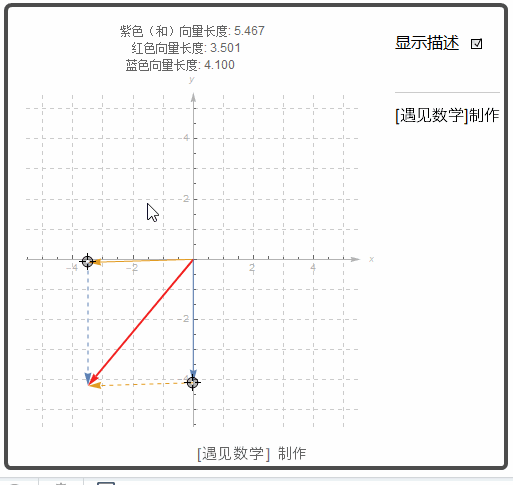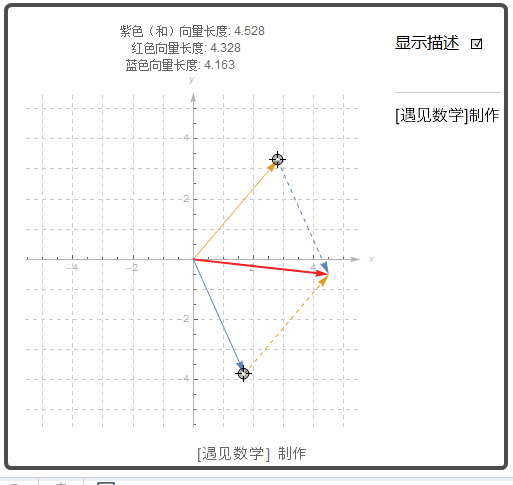
向量加法的另一种表示称为加法的平行四边形定律, 其中的和称为合成向量, 是平行四边形的对角线. 再物理学中, 力, 速度以及加速度等都是按向量的方式相加. 观察下图两个向量之和(红色箭头).![]() 一个标量 k 和向量 u 的乘积动画显示如下. 如果 k >0, 则 k u 与 u 有相同的方向; 若 k<0, 则 k u 和 u 有相反的方向.
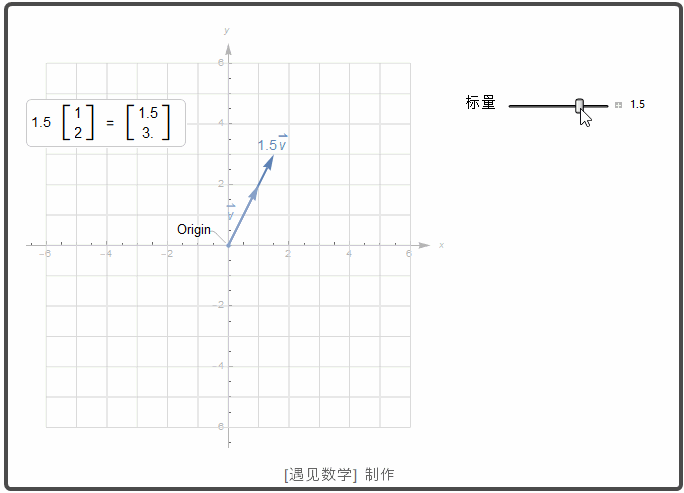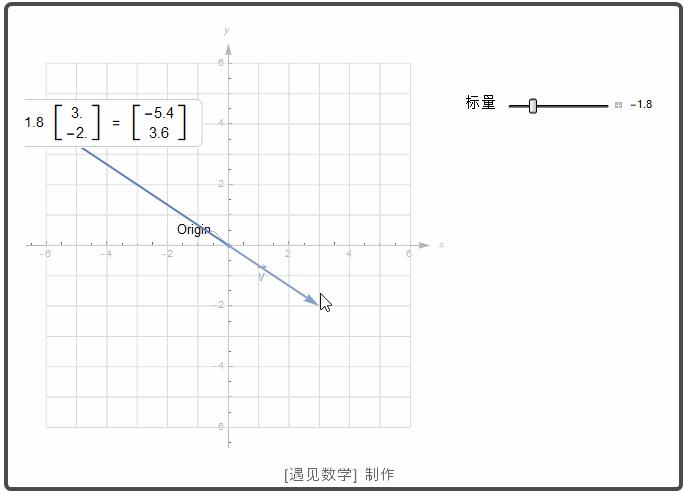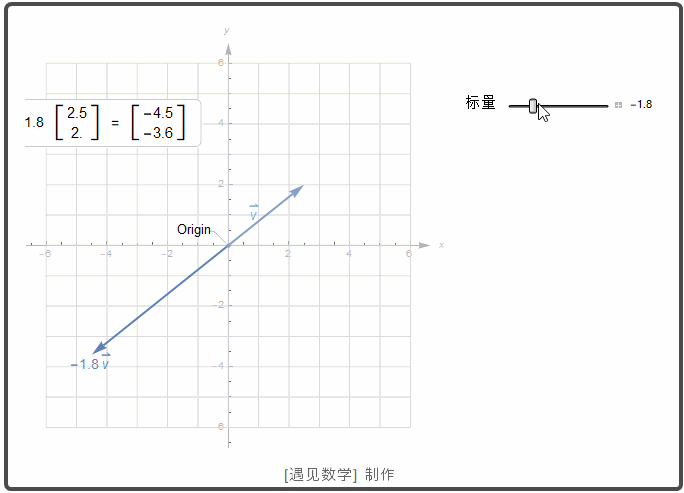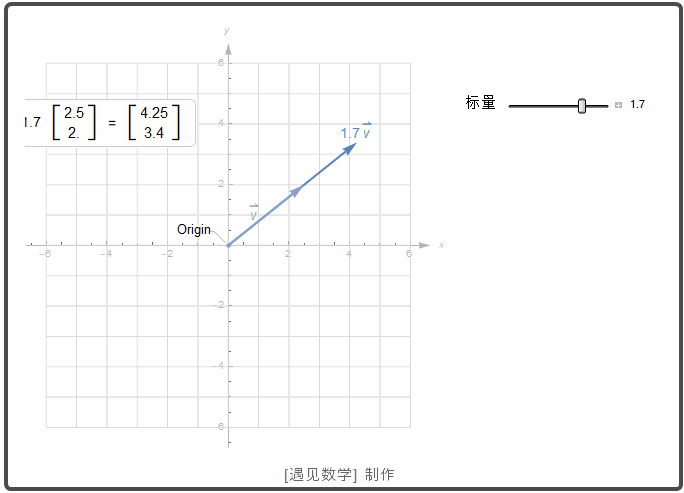
一个标量 k 和向量 u 的乘积动画显示如下. 如果 k >0, 则 k u 与 u 有相同的方向; 若 k<0, 则 k u 和 u 有相反的方向.
![]()
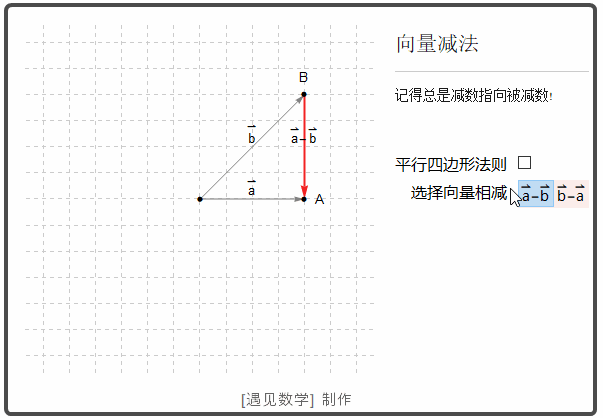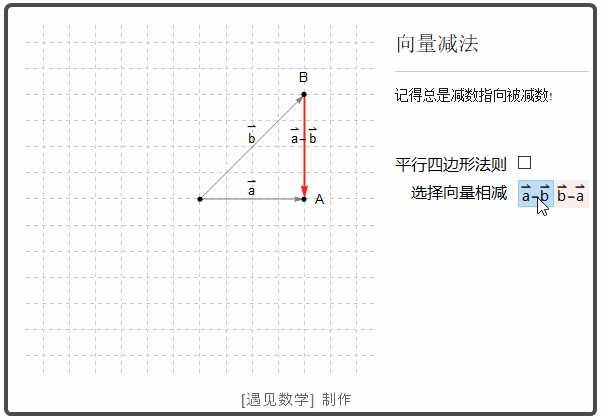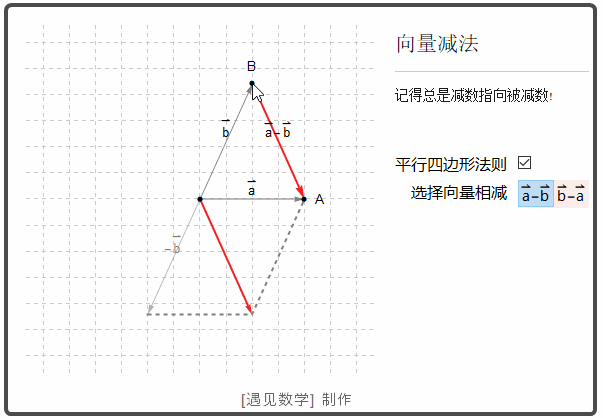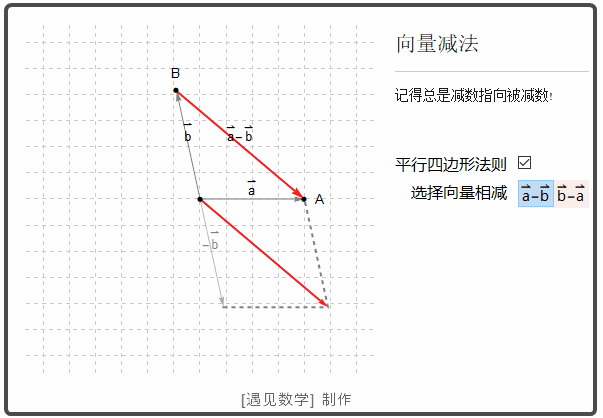
两个向量的差 u - v 意义是 u - v = u + (-v)
![]()
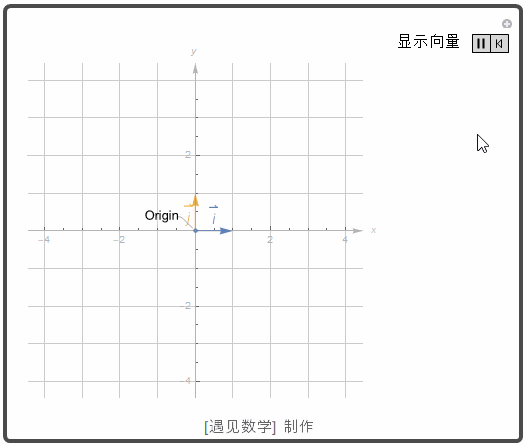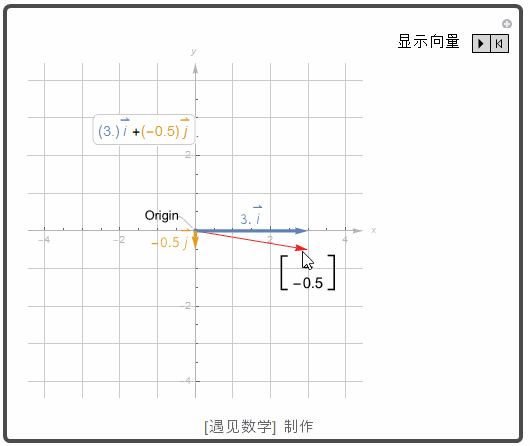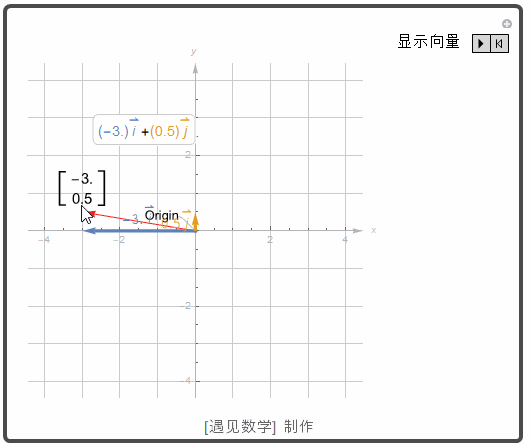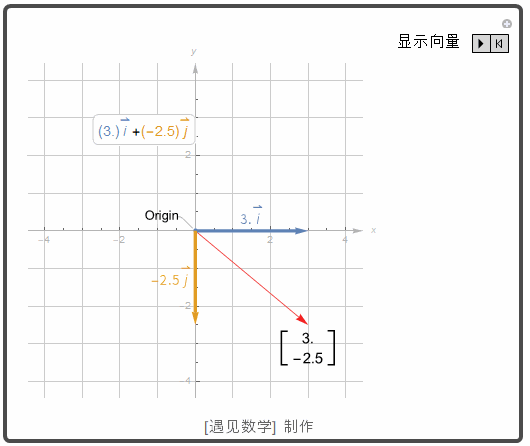
标准单位向量
任何平面向量 v=(a,b) 都可以写成标准单位向量 i=(1,0) 和 j=(0,1) 的如下的线性组合:v = (a,b) = (a,0) + (0,b) = a(1,0) + b(0,1) = a i + b j
![]()
长度和方向
在研究运动时, 经常想要知道一个物体朝什么方向和运行有多快. 向量 v≠0
v
≠
0
, 则 v|v|
v
|
v
|
是一个和 v 同方向的单位向量.
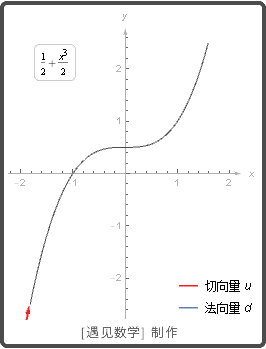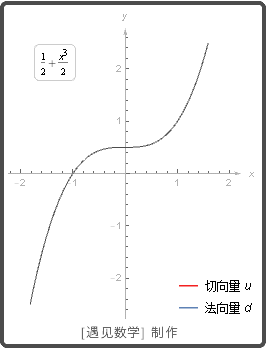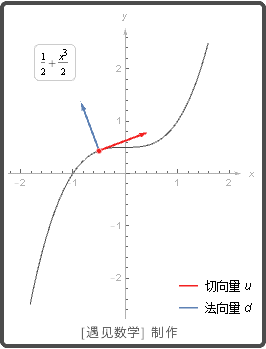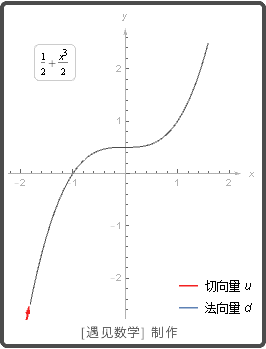
切线和法线
当一个物体沿平面(或空间)内的一个路径运动时, 它的速度是路径的一个切向量.
一个向量是一条曲线再一个点 P 的切向量或法向量, 如果它分别平行或垂直于曲线再点 P 的切线. 请观察下图动画:
![]()
点积
如果一个力 F 作用再一个路径运动的质点上. 我们经常需要知道力再运动方向的大小.
点积
两个非零向量 u=(u1,u2)
u=(
u
1
,
u
2
)
和 v=(v1,v2)
v=(
v
1
,
v
2
)
的点积(或内积)是数 u⋅v = u1v1+u2v2
u
⋅
v =
u
1
v
1
+
u
2
v
2
向量间的夹角
两个非零向量 u=(u1,u2)
u=(
u
1
,
u
2
)
和 v=(v1,v2)
v=(
v
1
,
v
2
)
的夹角由下面式子给出:
![]()
特别注意: 向量 u 和 v 是正交的, 当且仅当 u⋅v = 0
u
⋅
v = 0
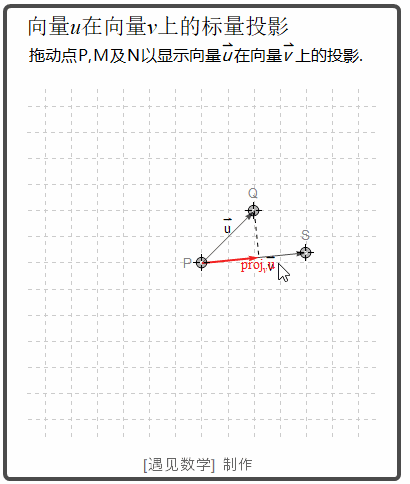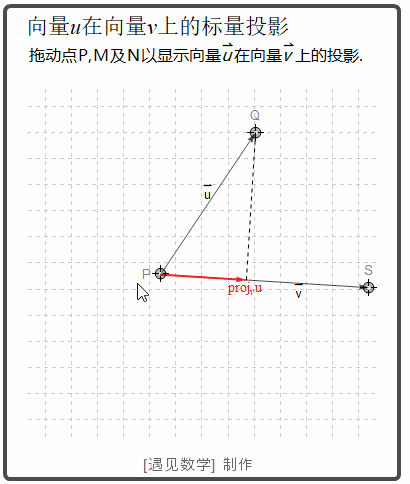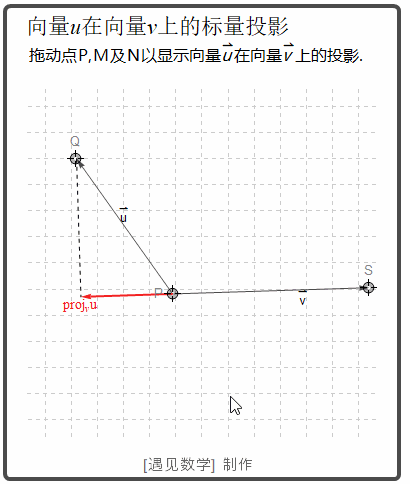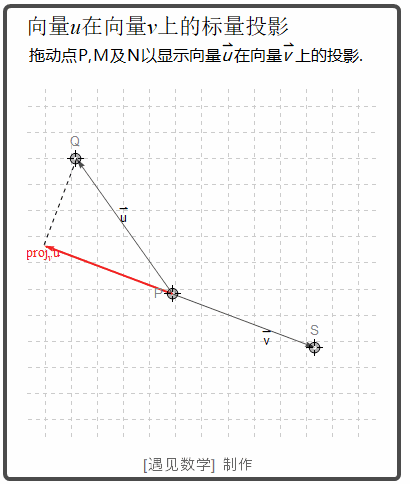
向量投影
下面看看向量 u 在 v 上的向量投影动画:
![]()
如果 u 和 v 之间的夹角 θ 是锐角, uprojv
u
proj
v
有长度 |u|cosθ
|
u
|
cos
θ
和方向 v|v|
v
|
v
|
; θ 是钝角, uprojv
u
proj
v
有长度 -|u|cosθ
-
|
u
|
cos
θ
和方向 −v|v|
−
v
|
v
|
把一个向量写成正交向量的和
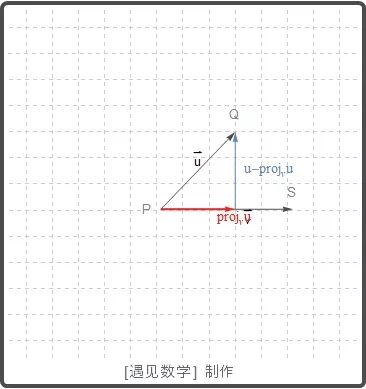
在研究一个质点沿平面上(或空间中)的一个路径的运动时, 加速度向量就可以写成它的切向分量和法向分量之和.
![]()
从图中可以看到对向量 u 和 v 而言, 从上图可以看到 u-projvu
u-
proj
v
u
正交于投影向量 uprojv
u
proj
v
, 于是 u = projvu + (u - projvu)
u =
proj
v
u + (u -
proj
v
u)
, 就把 u 表示成了正交向量的和.(完)
「予人玫瑰, 手留余香」
转发既是支持, 我们会努力走的更远!