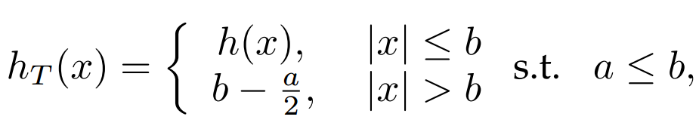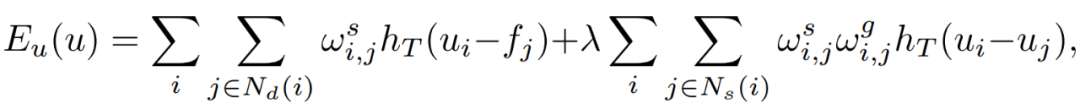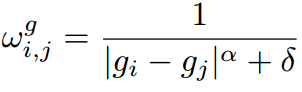【速览】TPAMI丨泛化边缘保持和结构保持图像平滑模型

2021 年 10 月 15 日 中国图象图形学学会CSIG

学会“成果速览”系列文章旨在将图像图形领域会议期刊重要成果进行传播，通过短篇文章让读者用母语快速了解相关学术动态，欢迎关注和投稿~

◆ ◆ ◆ ◆

泛化边缘保持和结构保持图像平滑模型

刘伟

^{1}

, 张平平

^{2}

, 雷印杰

^{3}

, 黄晓霖

^{4}

, 杨杰

^{4}

，Michael Ng

^{1}

^{1}

香港大学，

^{2}

大连理工大学，

^{3}

四川大学，

^{4}

上海交通大学

TPAMI

撰稿人：刘伟

通讯作者：杨杰，黄晓霖

推荐理事：林宙辰

原文标题：A Generalized Framework for Edge-Preserving and Structure-Preserving Image Smoothing

原文链接： https://arxiv.org/abs/2107.07058

原文代码链接: https://github.com/wliusjtu/Generalized-Smoothing-Framework

◆ ◆ ◆ ◆

摘要

图像平滑滤波是计算机视觉及图形图像学中非常重要的步骤。不同应用任务往往有着不同的平滑特性需求，然而当前大部分平滑滤波算法都有着固定的平滑特性，因此无法满足各种任务的不同需求。为了实现不同的平滑特性以满足不同的任务需求，本文首先引入了具有高度灵活性的截断Huber惩罚函数，基于该函数，我们进一步提出了能够适用于各种边缘保持和结构保持平滑滤波的泛化模型。我们的模型能够适用于各种任务并取得了当前最好的实验结果。针对所提出的非凸非光滑能量函数，我们提出了高效的优化求解算法，并在理论上证明我们的算法能够收敛。

研究背景

图 1 我们的算法可以应用于（a）图像细节增强，（b）卡通图压缩伪影去除，（c）引导深度图超分辨，（d）图像去纹理。这些任务需要不同甚至相对立的平滑特性。

图像平滑滤波在计算机视觉以及图形图像学领域有着广泛的应用，同时不同的应用任务往往对平滑滤波特性有着不同的需求。然而当前大部分滤波器其内在平滑特性往往是固定的，因此只能适用于部分任务，同时当前大部分算法并没有对应用任务作出明确分类，因此其应用场景并不是很明确。为此，我们首先将大部分应用任务分为以下四类。

第一类主要任务包括图像细节增强，高动态图像压缩等任务。这类任务要求能够平滑掉细节同时保留显著性边界。显著性边界既不能被模糊也不能被锐化，但是其幅值可以被压缩。显著性边界被模糊会引起晕轮现象（halos），而锐化会引起梯度翻转现象（gradient reversals）。

第二类任务包括卡通图压缩伪影去除，图像抽象画，仿铅笔画素描生成。这类任务要求能够去除细小结构的同时锐化显著图像边界，同时显著性边界的幅值不能被压缩。图1（b）展示了示例。

第三类为引导图像滤波，包括引导深度图超分辨和闪光/非闪光图像滤波等。这类任务的主要难点问题是对目标图和引导图结构不一致问题的鲁棒性，因为结构不一致会导致平滑后的图像存在纹理拷贝或者模糊边界的问题。同时由于目标图中往往含有噪音，因此这类任务还需要平滑后的图像边界能够被锐化，如图1（c）所示。

第四类任务主要为结构保持滤波任务，如图像去纹理。这类算法要求保持显著性结构即使其对应的边界很弱，同时平滑掉小的结构即使其对应的边界很强。这种平滑特性要求与前三类任务完全不同，前三类任务要求保持显著性边界，而第四类任务要求保持显著性结构。

为了更为详细的区分不同的平滑任务，我们将第一到第三类旨在保留边缘的任务归为保边平滑的范畴，而将第四种集中于保留结构的任务定义为结构保持的平滑。针对于这两种图像平滑，研究人员们提出了一系列平滑操作，但它们都是针对特定任务设计，能进行的平滑处理也相对固定，但目前几乎没有能同时处理以上四种平滑需求的操作。

为了提高平滑算法的适应性，我们提出了一种基于非凸非平滑的优化框架，可以实现多种不同功能的平滑，为上述四类平滑需求提供了统一的解决方案。并在各种任务中取得当前最好的实验结果。

算法原理

截断Huber惩罚函数

Huber惩罚函数的定义如下，可以看到在 $\mathrm{x}< a$ 的区域里表现为 $L_{2}$ 惩罚函数，而在大于 $a$ 的区域里则表现为 $L_{1}$ 惩罚函数。

而截断Huber则引入了一个新的参数 b 来对 x>b 的区域进行饱和处理，所有超过的值都将被限制在 b-a/2 的数值上：

截断Huber在不同的参数设置下可以灵活的表现出不同的特性。假设输入图像的强度范围在 $\left [ 0,I_{m} \right ]$ 之间，那么所有的边缘强度也会处于 $\left [ 0,I_{m} \right ]$ 之间。如果设置 $a=\varepsilon \left ( \varepsilon =1e-3 \right )$ ，在 $b>I_{m}$ 的情况下截断Huber就与Huber函数一样不会饱和，同时足够小的 a 也是在较小输入时表现出类似 $L_{1}$ 惩罚函数的特性；若设置 $b< I_{m}$ 则截断Huber就会在边缘强度达到最大值 $I_{m}$ 前饱和，使得它在惩罚弱边缘的同时不惩罚强边缘，从而可以锐化强边缘。这意味着 b 可以作为调节截断Huber函数是否锐化边缘的开关。另一方面如果设置 $a=b>I_{m}$ 或 $a=b< I_{m}$ ，此时函数表现出 $L_{2}$ 惩罚函数的特性而 a 变成了普通 $L_{2}$ 惩罚函数和截断 $L_{2}$ 惩罚函数的开关。图2展示了不同参数下的截断Huber函数。

图 2 不同参数下的截断Huber惩罚函数

模型

通过使用截断Huber惩罚函数的高度灵活性，我们可以有效构建一个高效的目标函数来实现多功能的平滑处理。在给定输入图像f和引导图像 g 的前提下，输出图像 u 是下列目标函数的解：

其中 $h_{T}\left ( \cdot\right )$ 为截断Huber惩罚函数，为了方便，我们分别使用 $\left \{ a_{d},b_{d} \right \}$ 和 $\left \{ a_{s},b_{s} \right \}$ 分别表示上述能量函数中数据项和平滑项中截断Huber惩罚函数 $h_{T}\left ( \cdot\right )$ 的参数。 $N_{d}\left ( i \right )$ 和 $N_{s}\left ( i \right )$ 分别是以像素 $i$ 为中心的半径为 $r_{d}$ 和 $r_{s}$ 的近邻。 $w_{i,j}^{s}$ 和 $w_{i,j}^{g}$ 分别定义如下：

其中 g 表示引导图像，可以为输入图像f， $\delta =1e-3$ 。

通过对 $\left \{ a_{d},b_{d} \right \}$ ， $\left \{ a_{s},b_{s} \right \}$ $r_{d}$ ， $r_{s}$ ， $\alpha$ 以及引导图像 g 进行不同的组合，上述模型可以实现不同的平滑特性，即我们模型的不同模态，以实现处理不同类型的应用任务。具体参数设置如下表：

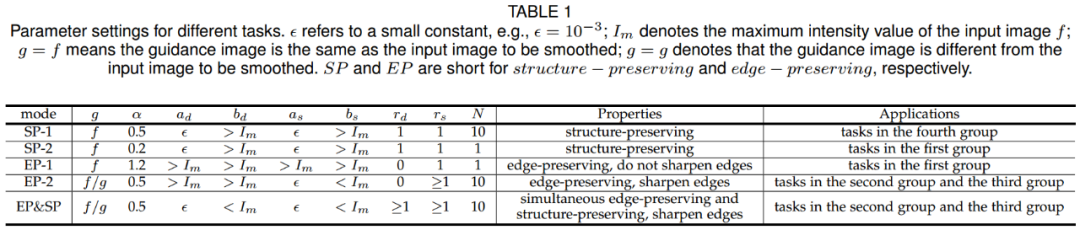
我们模型不同模态下的平滑特性在一维信号中的示意图如图3。具体分析可参考我们的文章第3.4章节。

图 3 我们的模型不同模态一维信号平滑示意图以及与当前最好算法对比

实验结果及对比

我们将所提出的模型应用于所提出的四类任务。在第一类任务中，我们应用于图像细节增强和高动态图像压缩，实验结果如图4和图5所示。可以看出我们算法在抑制该类应用中的晕轮和梯度翻转挑战问题中有着很好的表现。

图 4 图像细节增强实验结果及对比

图 5 高动态图像压缩实验结果及对比

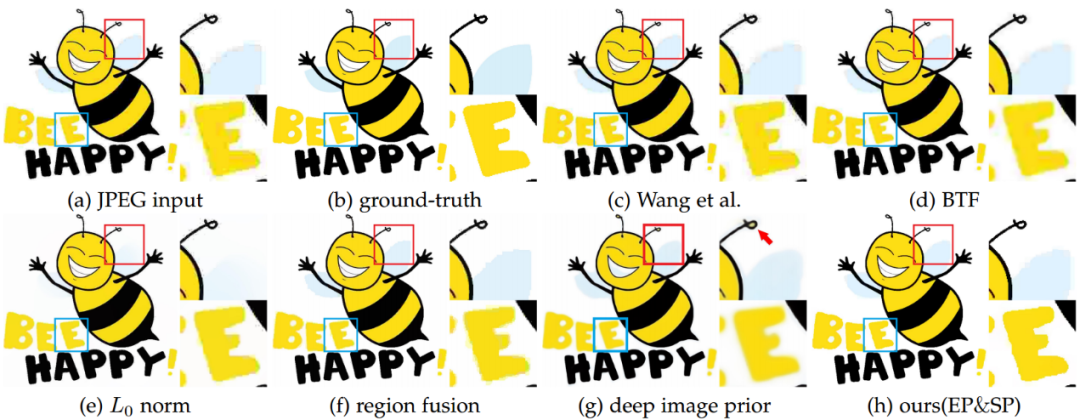
对于第二类任务，我们将算法应用于卡通图去压缩伪影，实验结果如图6所示。从结果中可以看出我们的算法对于锐化强边界和保持弱边界方面都有着很好的表现。

图 6 去卡通图压缩伪影实验结果及对比

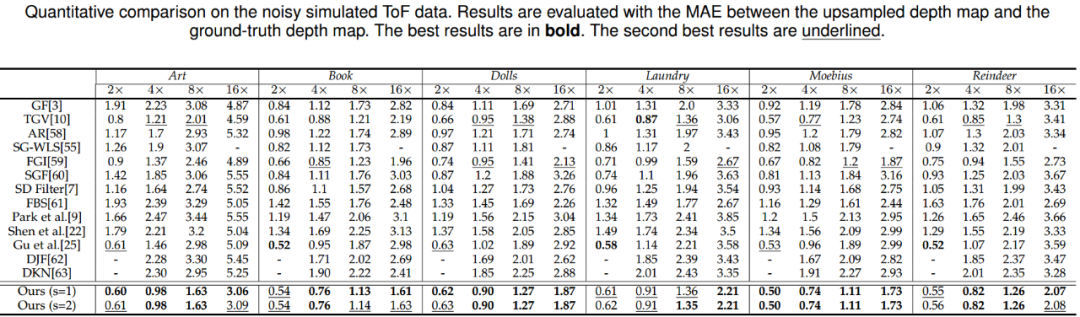
对于第三类任务，我们将算法应用于引导深度图超分辨，实验结果及对比如图7所示，同时下列表格中展示了量化对比。可以看出我们的算法取得了当前最好的实验结果。

图 7 引导深度图超分辨实验结果及对比

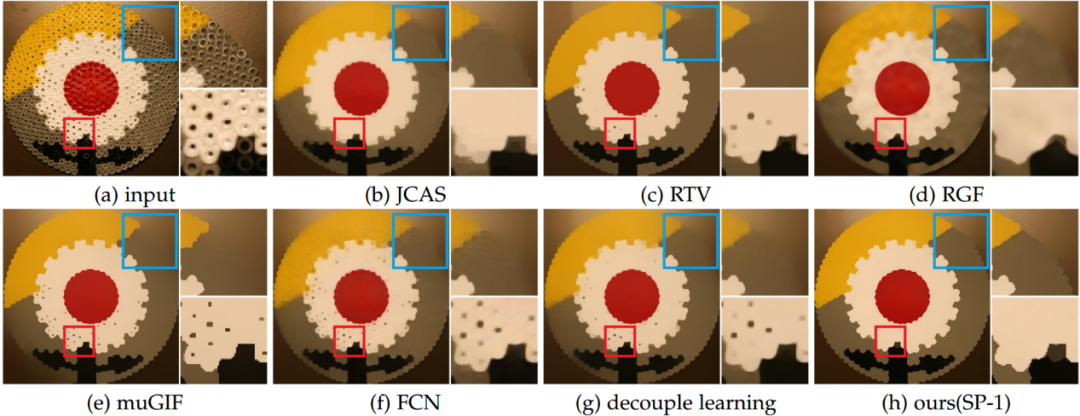
对于第四类任务，我们将算法应用于图像去纹理，实验结果及对比如图8所示。可以看出我们的算法在去除强边界的小纹理结构和保持弱边界的大纹理结构方面有着优于其他算法的表现。

图 8 图像去纹理实验结果及对比

结论

在本文章中，我们提出了一种可用于边缘保持和结构保持的平滑滤波算法。我们首先引入了截断Huber惩罚函数，该惩罚函数具有高度灵活性，在不同参数下具有不同的惩罚特性。基于该灵活性，我们进一步提出了高度泛化的图像平滑算法。该算法可用于不同任务，实现不同的平滑特性，这与以往提出的图像平滑算法是截然不同的。我们的算法甚至能够实现之前算法无法实现的平滑特性，因此我们的算法可以处理更具挑战性的任务。同时我们提出的求解算法能够高效的优化所提出的非凸非光滑优化问题。通过大量实验，我们对所提出的算法的有效性进行了充分的验证。

参考文献

[1] Z. Farbman, R. Fattal, D. Lischinski, and R. Szeliski, “Edgepreserving decompositions for multi-scale tone and detail manipulation,” in ACM Transactions on Graphics (TOG), vol. 27, no. 3. ACM, 2008, p. 67.

[2] K. He, J. Sun, and X. Tang, “Guided image filtering,” IEEE Transactions on Pattern Analysis and Machine Intelligence (TPAMI), vol. 35, no. 6, pp. 1397–1409, 2013.

[3] L. Xu, C. Lu, Y. Xu, and J. Jia, “Image smoothing via l 0 gradient minimization,” in ACM Transactions on Graphics (TOG), vol. 30, no. 6. ACM, 2011, p. 174.

[4] B. Ham, M. Cho, and J. Ponce, “Robust guided image filtering using nonconvex potentials,” IEEE Transactions on Pattern Analysis and Machine Intelligence (TPAMI), vol. 40, no. 1, pp. 291–307, 2018.

[5] L. Xu, Q. Yan, Y. Xia, and J. Jia, “Structure extraction from texture via relative total variation,” ACM Transactions on Graphics (TOG), vol. 31, no. 6, p. 139, 2012.

[6] W. Liu, X. Chen, J. Yang, and Q. Wu, “Robust color guided depth map restoration,” IEEE Transactions on Image Processing (TIP), vol. 26, no. 1, pp. 315–327, 2017.

[7] J. Kopf, M. F. Cohen, D. Lischinski, and M. Uyttendaele, “Joint bilateral upsampling,” in ACM Transactions on Graphics (ToG), vol. 26, no. 3. ACM, 2007, p. 96.

[8] E. S. Gastal and M. M. Oliveira, “Adaptive manifolds for real-time high-dimensional filtering,” ACM Transactions on Graphics (TOG), vol. 31, no. 4, p. 33, 2012.

[9] E. S. Gastal and M. M. Oliveira, “Domain transform for edge-aware image and video processing,” in ACM Transactions on Graphics (TOG), vol. 30, no. 4. ACM, 2011, p. 69.

[10] C. Tomasi and R. Manduchi, “Bilateral filtering for gray and color images,” in IEEE International Conference on Computer Vision (ICCV). IEEE, 1998, pp. 839–846.

[11] W. Liu, P. Zhang, X. Huang, J. Yang, C. Shen, and R. Ian, “Real-time image smoothing via iterative least squares,” ACM Transactions on Graphics (TOG), 2020.

[12] Q. Fan, D. Chen, L. Yuan, G. Hua, N. Yu, and B. Chen, “Decouple learning for parameterized image operators,” in Proceedings of the European Conference on Computer Vision (ECCV), 2018, pp. 442–458.

[13] D. Ulyanov, A. Vedaldi, and V. Lempitsky, “Deep image prior,” in Proceedings of the IEEE conference on Computer Vision and Pattern Recognition (CVPR), 2018, pp. 9446–9454.

[14] Y. Li, J.-B. Huang, N. Ahuja, and M.-H. Yang, “Joint image filtering with deep convolutional networks,” IEEE Transactions on Pattern Analysis and Machine Intelligence (TPAMI), vol. 41, no. 8, pp. 1909–1923, 2019.