进展 | 硼也能形成蜂窝状二维晶格结构

2018 年 8 月 5 日 中科院物理所

硼烯是指由硼元素构成的二维平面结构，其存在的可能性一直受到理论研究者的强烈关注。由于硼原子只有三个价电子，与石墨烯类似的蜂窝状结构并不是一种能量上稳定存在的硼烯结构。相反，以三角形密堆积晶格为基础的孔洞型结构是可以稳定存在的。2016年，中国科学院物理研究所/北京凝聚态物理国家研究中心表面物理国家重点实验室SF09组吴克辉研究员、陈岚研究员等率先利用超高真空分子束外延（MBE）直接进行单原子层构筑的方法，在Ag(111)衬底上获得了这种理论上期待已久的单层硼烯，并发现硼烯的多种相，对应于三角晶格中不同周期的孔洞结构（Nature Chem. 8, 564 (2016)）。

然而，蜂窝状结构的硼烯仍然受到研究者的强烈关注。首先，独特的二维六角蜂窝状结构天然赋予硼烯狄拉克锥的能带结构。于是，大多数在石墨烯中发现的新奇量子效应，都有望在硼烯中获得相应的体现，例如无质量、手性、相对论性的电子在电场与磁场中表现出的反常的物理现象，极高的载流子迁移率等。其次，规则的六角蜂窝状结构的硼原子层在自然界中其实是存在的。人们所熟知的超导材料二硼化镁就是由六角蜂窝状结构的硼原子层与三角密堆积结构的镁原子层交替排列形成的。二硼化镁的超导电性来源于电声子耦合，其中金属性的硼原子层起关键作用。因此，六角蜂窝状结构的硼烯甚至有可能实现二维超导性。但是，二硼化镁并非层状结构，其中的硼原子层无法独立存在。

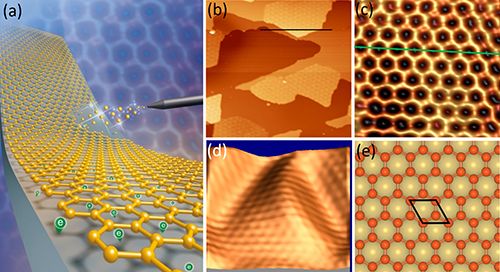
考虑到硼相比于碳原子，缺少一个最外层电子，要想获得稳定的蜂窝状硼烯，必须要往硼烯中掺入大量的电子，而基底与硼烯之间的界面电荷转移是往硼烯中掺入电子的最有效途径之一。基于上述原因，SF09组的吴克辉研究员、陈岚研究员、程鹏副研究员带领博士研究生黎文彬、孔龙娟等人，继续深入开展硼烯薄膜的制备工作。他们采用单晶Al(111)作为基底，通过生长过程的精确控制，最终成功地制备出了蜂窝状结构的硼烯薄膜（图1b）。他们利用高分辨的扫描隧道显微镜（STM）观察到了硼烯完美的六角蜂窝状结构（图1c），晶格周期为0.29 nm，与理论预言中自由状态下蜂窝状硼烯的0.3 nm晶格周期接近。由于局域应力的存在，硼烯薄膜还呈现出具有较大周期的三角形周期性起伏结构（图1d），但这并不影响硼烯本身的蜂窝状晶格。同时，这种蜂窝状结构在跨越衬底的台阶时也保持了连续不间断的特点，为硼烯的单层平面蜂窝状结构提供了又一有力佐证。

以往的理论计算表明由于电子的缺失，自由状态下蜂窝状硼烯并不能稳定存在，但在单晶Al(111)基底上却成功地实现了这一结构的单层硼烯，说明Al(111)作为基底起到十分重要的作用。通过第一性原理的计算，发现了Al(111)基底与硼烯中每个硼原子间有近1个电子的电荷转移，这有效地解决了蜂窝状结构的二维硼烯中电子的缺失，对于蜂窝状硼烯的稳定存在起到至关重要的作用。

该工作发现硼原子形成的一种全新的同质异形结构，实现了学术界期待已久的平面六角蜂窝状结构的硼烯，美国Rice大学的理论化学家Boris Yakobson教授专门为此撰写了评论文章，形象地将其称为“铝锅上的炼金术”（Science Bulletin 63, 270 (2018)）。同时该工作也为进一步研究硼烯中可能存在的奇异电子特性包括狄拉克锥形能带结构、超导电性等奠定了基础，而且为实现基于硼烯的电子器件提供了诱人的前景。该工作发表在Science Bulletin 63, 282 (2018)上，并以“Boron can form a purely honeycomb 2D structure”为题作为当期的封面文章报道。

以上研究工作得到了国家重点研发计划、国家自然科学基金和中科院战略性先导科技专项的支持。

图1：(a) 利用超高真空分子束外延（MBE）的制备方法在Al(111)衬底上制备出蜂窝状结构硼烯的示意图（Science Bulletin封面图）；(b)(c)(d) Al(111)衬底上硼烯薄膜的扫描隧道显微镜（STM）图，其中d图显示出三角形的周期性起伏结构；(e) Al(111)衬底上硼烯薄膜的原子结构模型图。

编辑：loulou

近期热门文章Top10

↓ 点击标题即可查看 ↓

1. 正版印度神药为何这么贵？研究半世纪，两夺世界第一，出了五位顶级医学奖

2. 吃瓜时节，我们用公式计算告诉你，如何科学地挑选西瓜！

3. 一个64G的手机，装满文件后会变重吗？| No.114

4. 为什么三体不稳定，我们的太阳系如此稳定？

5. 世界杯伪球迷实用装 X 指南

6. 为什么空调吹出的风有一股“空调味”？| No.111

7. 火星上真的有水！“火星快车”探测到直径20千米的液态水湖泊

8. 这道像是奥数题的“填色问题”，至今无人能解决

9. 为什么奥利奥扭开以后，夹心总是粘在其中一面上？