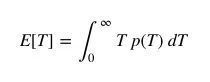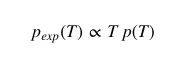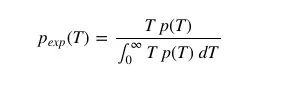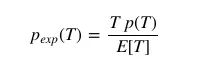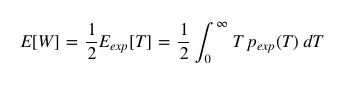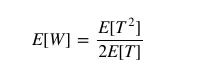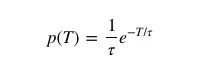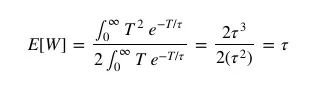等待时间悖论:为什么我的公交车总是迟到?
编者按:在数据科学领域,值得阅读的好书有很多,尤其是O‘Reilly出版的一系列动物封面英文书。其中一本“蜥蜴书”叫《Python数据科学指南》(Python Data Science Handbook),书中详细介绍了Jupyter、Numpy、Pandas、数据可视化和scikit-learn模块的具体使用方式,是新手入门机器学习的一条捷径。近日,这本书的作者Jake VanderPlas写了一篇博文,深入浅出地介绍了一个有趣的概念:等待时间悖论。
图像来源:维基百科 许可:CC-BY-SA 3.0
经常乘坐公共交通工具的人可能都遇到过这种情况:
你到公交站台等车,标牌显示公交车的发车间隔是10分钟一辆。你瞥了眼手表,记下时间……11分钟后,公交车终于来了,你不由开始懊恼:为什么我老是这么倒霉!
已知公交车每隔10分钟发一班,你到站台是在某个随机时间点(不借助实时公交APP),面对这种情况,很多人会想当然地觉得自己的平均等待时间应该是5分钟。但实际上,5分钟后,公交车没来,这时你只能继续等;10分钟后,车子可能还是没有来……在一些合理的数学假设下,你可以得出一个惊人结论:
当公交车的平均发车间隔是10分钟时,乘客平均等公交车的时间也会是10分钟。
这就是等待时间悖论。
那么这个悖论真实存在吗?这些“合理的假设”究竟是只流于理论,还是同样适用于现实?本文会以美国西雅图市的真实公交车到达时间数据为例,从模拟和概率论证的角度探讨这个问题。
检验悖论(Inspection Paradox)
如果每隔10分钟一定有一班车到这个站台,那我们的平均等待时间确实是这个间隔的一半:5分钟。但是,如果10分钟只是个平均值,乘客的平均等待时间其实会比5分钟更长一些,这点不难理解。
等待时间悖论其实是检验悖论的一个特殊例子,后者在日常生活中更普遍。举一个简单例子,假设你正在调查某大学的班级规模,调查方法是随机选一些学生问“你所在的班级有多少人”再计算平均值,最后你统计出的结果是平均56人。但是,全校的班级平均人数实际上只有36(以上数据来自普渡大学调查)。这不是说有人撒了谎,而是10人班级和100人班级被抽样的概率不一样,随机抽样会导致对人数较多的班级过度抽样,使结果向人多的一方倾斜。
同理,在平均每隔10分钟就有一班车到站台的情况下,有时前后两辆公交车的到达间隔会超过10分钟,有时候不到10分钟,如果你到站台是个随机时间点,你就有更大概率会遇到超过10分钟的情况。所以乘客的平均等待时间更长是有道理的,因为较长间隔被过度采样了。
但等待时间悖论提出了一个更令人“匪夷所思”的结论:当前后两辆车的平均到站间隔是N分钟时,乘客体验到的公交车平均到站间隔是2N分钟。这会是真的吗?
模拟等待时间
为了证明等待时间悖论的结论是正确的,首先我们可以模拟一些公交车,它们的平均到站时间是10分钟。已知样本数量越大,结果越准确,我们设一共有100万辆公交车。:
import numpy as np
N = 1000000 # 公交车数量
tau = 10 # 平均到站间隔
rand = np.random.RandomState(42) # 随机种子
bus_arrival_times = N * tau * np.sort(rand.rand(N))
接着,我们检查一下它们的平均到站间隔是否接近τ=10:
intervals = np.diff(bus_arrival_times)
intervals.mean()
输出:9.9999879601518398
模拟好了公交车,之后是模拟大量在这个时间跨度内到达公交站的乘客,并计算他们每个人的等待时间。如下所示,我们把它封装进一个函数以备后用:
def simulate_wait_times(arrival_times,
rseed=8675309, # Jenny的随机种子
n_passengers=1000000):
rand = np.random.RandomState(rseed)
arrival_times = np.asarray(arrival_times)
passenger_times = arrival_times.max() * rand.rand(n_passengers)
# 为每个模拟乘客找到下一辆公交车
i = np.searchsorted(arrival_times, passenger_times, side='right')
return arrival_times[i] - passenger_times
然后我们可以模拟一些等待时间并计算平均值:
wait_times = simulate_wait_times(bus_arrival_times)
wait_times.mean()
输出:10.001584206227317
正如等待时间悖论预测的那样,乘客的平均等待时间也接近10分钟。
深入挖掘:概率和泊松过程
所以上面的代码到底是什么意思?
从本质上看,等待时间悖论是检验悖论的一个特例,观察某个值的概率和这个值本身有关。让我们用p(T)表示公交车到站时间间隔T的分布,这时,对到达时间的期望值是:
在上面的例子中,我们已经设E[T]=τ=10分钟。
当乘客在随机时间点到达公交站时,他们经历的等待时间的概率既会受p(T)影响,又会受T本身影响:汽车到达间隔越长,乘客遇到较长等待时间的概率也会相应变大。
所以我们可以写出乘客感受到的汽车到站间隔分布:
它们的比例常数是:
也就是:
已知乘客的期望等待时间E[W]是他们体验到的公交车到站间隔的一半,我们可以把它写成:
改写上式可得:
现在剩下的就是为p(T)选择一个列表,并计算积分。
选择p(T)
我们可以通过绘制公交车到站间隔直方图来模拟p(T)的分布:
%matplotlib inline
import matplotlib.pyplot as plt
plt.style.use('seaborn')
plt.hist(intervals, bins=np.arange(80), density=True)
plt.axvline(intervals.mean(), color='black', linestyle='dotted')
plt.xlabel('Interval between arrivals (minutes)')
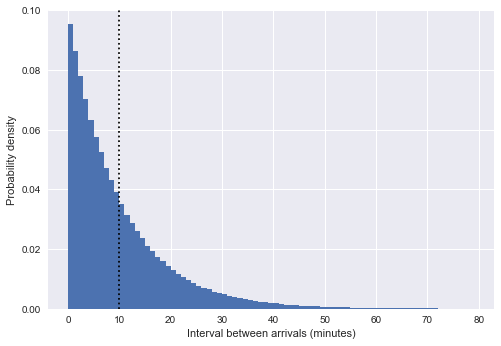
plt.ylabel('Probability density');
图中虚线表示平均到站时间为10分钟。可以发现,上图分布形状很像指数分布,这并不是偶然:我们把公交车到站间隔模拟成均匀随机数的做法十分类似泊松过程,而如果构成泊松过程,到站间隔的分布一定符合指数分布。
注:在我们的例子里,到站间隔分布只是近似指数分布。
如果到站间隔符合指数分布,它就遵循泊松过程——为了验证这个推理,我们可以用另一个泊松过程的属性来检查:在固定时间范围内,公交车到站次数的分布满足泊松分布。我们可以在之前的模拟中查看每小时公交车的到站次数:
from scipy.stats import poisson
# 计算1小时内公交车到站次数
binsize = 60
binned_arrivals = np.bincount((bus_arrival_times // binsize).astype(int))
x = np.arange(20)
# 绘制结果
plt.hist(binned_arrivals, bins=x - 0.5, density=True, alpha=0.5, label='simulation')
plt.plot(x, poisson(binsize / tau).pmf(x), 'ok', label='Poisson prediction')
plt.xlabel('Number of arrivals per hour')
plt.ylabel('frequency')
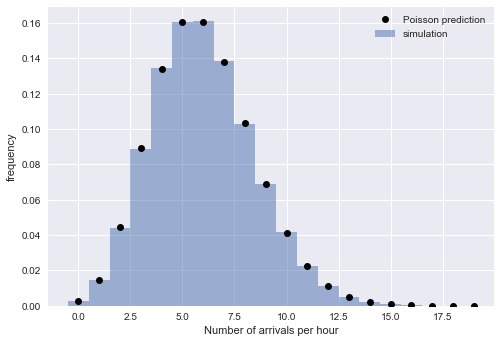
plt.legend();
如上图所示,模拟次数分布(方柱)和泊松分布(黑点)几乎一致。现在理论、模拟实践都支持这么一个事实:对于一个足够大的N,公交车的到站间隔可以用泊松过程描述,到站间隔分布满足指数分布。
这意味着我们可以把概率分布写成:
把上式带入之前的等式,可得每名乘客的平均等待时间是:
因此,如果公交车的到站间隔符合泊松过程,乘客的平均期望等待时间和公交车的平均到站间隔相同。
推断这个结论的另一种补充方法是:泊松过程是一个无记忆过程,这意味事历史事件与下一事件发生的预期时间无关。所以当你到达公交站时,你对下一班车的平均等待时间始终是一样的:不管前一班车是什么时候来的,你平均都得等10分钟。同理,无论你之前已经等了多久,乘客对下一班车的预期等待时间还是10分钟。
现实中的等待时间
那么泊松过程能描述现实生活中的公交车到站时间吗?
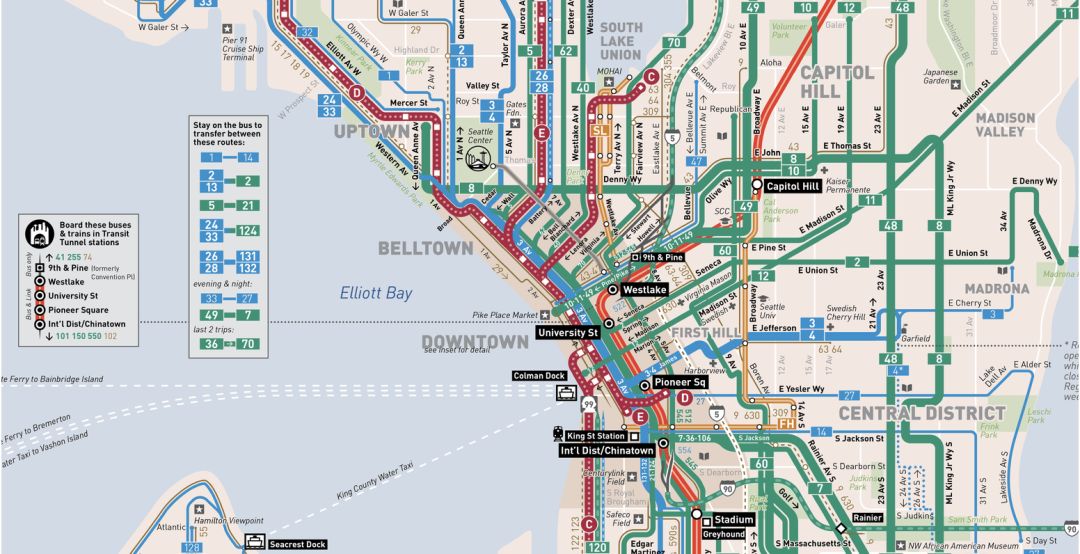
为了探讨等待时间悖论和现实情况是否存在矛盾,我们可以用一些数据进行更深入的研究(arrival_times.csv,3MB CSV文件)。这个数据集包含2016年第二季度美国西雅图3rd & Pike公交站的记录,它一共有3条快速线:C、D和E,给出了每辆公交车的预定和实际到达时间。
import pandas as pd
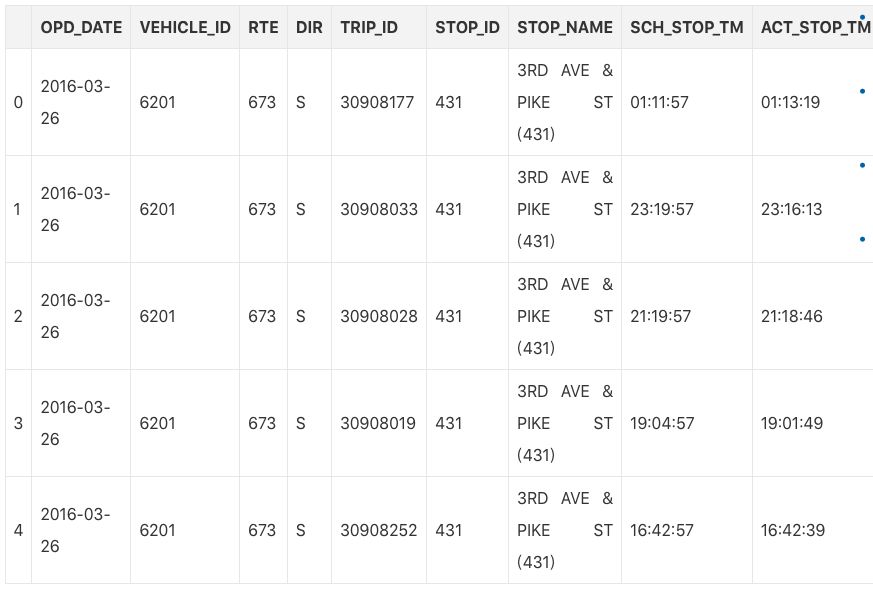
df = pd.read_csv('arrival_times.csv')
df = df.dropna(axis=0, how='any')
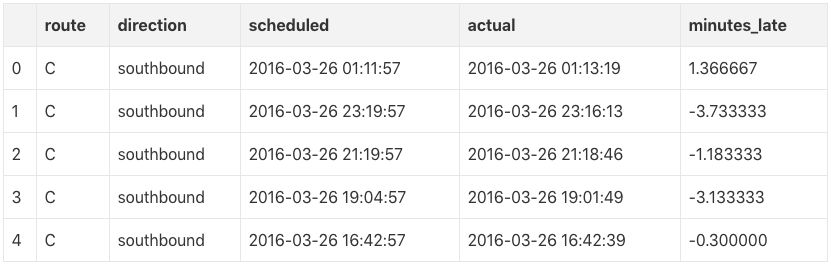
df.head()
之所以选择快速线,是因为在一天的大部分时间里,这几路公交车的到站间隔都稳定在10-15分钟之间。
数据清理
首先,让我们简单做一些数据清理,把数据集里的表格转成更易于使用的形式:
# 把日期和时间组合成单个时间戳
df['scheduled'] = pd.to_datetime(df['OPD_DATE'] + ' ' + df['SCH_STOP_TM'])
df['actual'] = pd.to_datetime(df['OPD_DATE'] + ' ' + df['ACT_STOP_TM'])
# 如果公交车的预计到点和实际到点过了半夜,需要调整日期
minute = np.timedelta64(1, 'm')
hour = 60 * minute
diff_hrs = (df['actual'] - df['scheduled']) / hour
df.loc[diff_hrs > 20, 'actual'] -= 24 * hour
df.loc[diff_hrs < -20, 'actual'] += 24 * hour
df['minutes_late'] = (df['actual'] - df['scheduled']) / minute
# 内外部路径映射
df['route'] = df['RTE'].replace({673: 'C', 674: 'D', 675: 'E'}).astype('category')
df['direction'] = df['DIR'].replace({'N': 'northbound', 'S': 'southbound'}).astype('category')
# 抓取有用的列
df = df[['route', 'direction', 'scheduled', 'actual', 'minutes_late']].copy()
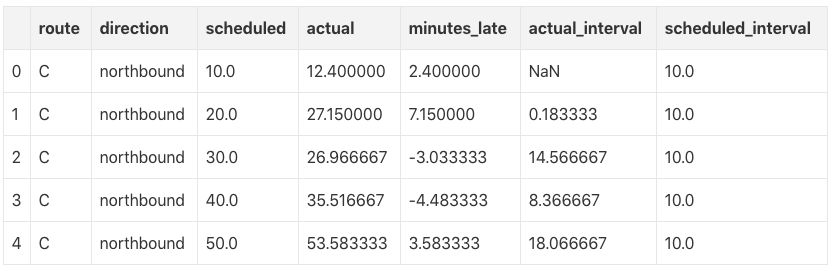
df.head()
公交车晚点情况
数据集中有6组不同数据:南向行驶和北向行驶的3路公交车。为了感受它们的早到/迟到特点,我们可以用实际到达时间减去预期到达时间,绘制6幅公交车“晚点”情况图:
import seaborn as sns
g = sns.FacetGrid(df, row="direction", col="route")
g.map(plt.hist, "minutes_late", bins=np.arange(-10, 20))
g.set_titles('{col_name} {row_name}')
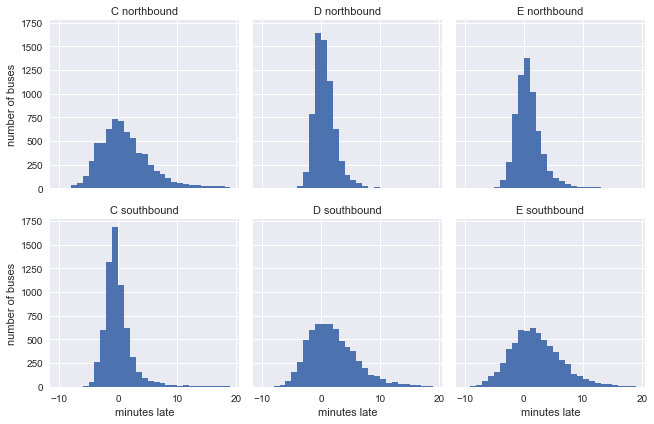
g.set_axis_labels('minutes late', 'number of buses');
事实上,很多人仅凭经验就知道公交车在刚发车后的一段时间内更不容易晚点,公交站越靠后,车子晚点的可能性就越大,晚点时间也越长。这一点在上图中得到了证实,南向行驶的C路公交车(图四)、北向行驶的D路公交车(图二)和北向行驶的E路公交车在刚开出时还很准时,到最后却出现了晚点超过十几分钟的情况。
预计到点和实际到点
接着,我们来看看这6条线路的实际到站间隔,这可以用Pandas的groupby函数计算:
def compute_headway(scheduled):
minute = np.timedelta64(1, 'm')
return scheduled.sort_values().diff() / minute
grouped = df.groupby(['route', 'direction'])
df['actual_interval'] = grouped['actual'].transform(compute_headway)
df['scheduled_interval'] = grouped['scheduled'].transform(compute_headway)
g = sns.FacetGrid(df.dropna(), row="direction", col="route")
g.map(plt.hist, "actual_interval", bins=np.arange(50) + 0.5)
g.set_titles('{col_name} {row_name}')
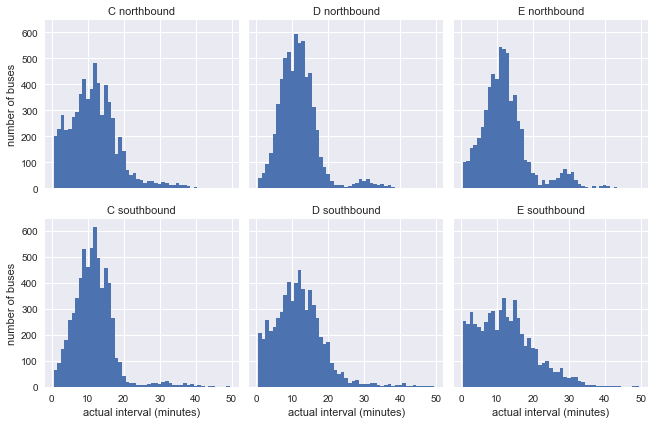
g.set_axis_labels('actual interval (minutes)', 'number of buses');
很明显,上述分布和指数分布差距比较大,但它存在一个潜在影响因素,就是影响实际到站间隔的预期到站间隔可能本身就是不恒定的。
所以我们得再去看看预期到站间隔的情况:
g = sns.FacetGrid(df.dropna(), row="direction", col="route")
g.map(plt.hist, "scheduled_interval", bins=np.arange(20) - 0.5)
g.set_titles('{col_name} {row_name}')
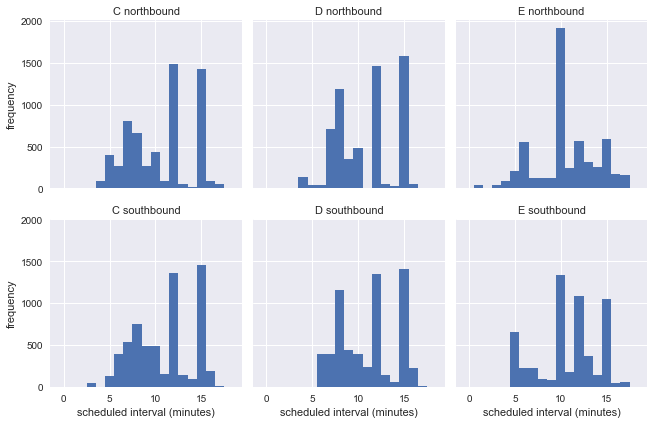
g.set_axis_labels('scheduled interval (minutes)', 'frequency');
很显然,预期到站间隔不是一个固定值,而且它的变化范围还很大。所以在这个数据集里,我们没法用实际到站间隔的分布来评估等待时间悖论是否准确。
构建同一时间表
虽然预期到站间隔不均匀,但它们中也存在一些常见的特定间隔,比如数据集中有近2000辆北向行驶的E路车的预期间隔是10分钟。为了探究等待时间悖论是否,我们可以按公交路线、行驶方向和预期到站间隔对数据集进行分类,筛选出相似的数据重新进行堆叠分析,假设它们是连续发车的。
def stack_sequence(data):
# first, sort by scheduled time
data = data.sort_values('scheduled')
# re-stack data & recompute relevant quantities
data['scheduled'] = data['scheduled_interval'].cumsum()
data['actual'] = data['scheduled'] + data['minutes_late']
data['actual_interval'] = data['actual'].sort_values().diff()
return data
subset = df[df.scheduled_interval.isin([10, 12, 15])]
grouped = subset.groupby(['route', 'direction', 'scheduled_interval'])
sequenced = grouped.apply(stack_sequence).reset_index(drop=True)
sequenced.head()
利用这些清理过的数据,我们可以绘制每个公交路线、行驶方向和到站频率的公交车“实际”到站间隔分布:
for route in ['C', 'D', 'E']:
g = sns.FacetGrid(sequenced.query(f"route == '{route}'"),
row="direction", col="scheduled_interval")
g.map(plt.hist, "actual_interval", bins=np.arange(40) + 0.5)
g.set_titles('{row_name} ({col_name:.0f} min)')
g.set_axis_labels('actual interval (min)', 'count')
g.fig.set_size_inches(8, 4)
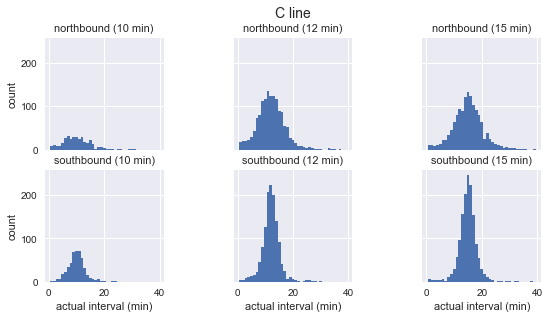
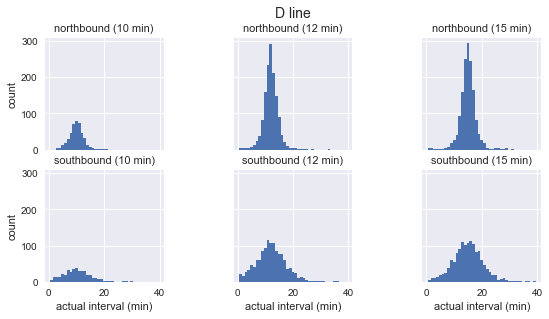
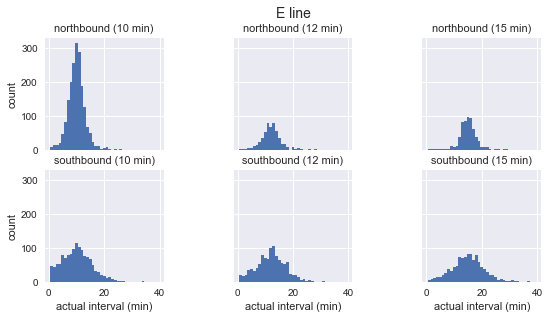
g.fig.suptitle(f'{route} line', y=1.05, fontsize=14)
如上图所示,这三路公交车的到站间隔分布近似高斯分布:在预期到站间隔附近达到峰值,一开始标准偏差较小,越往后越大。所以很显然,这和等待时间悖论的基石——指数分布相违背。
我们再用上面的数据计算每个公交路线、行驶方向和到站频率的公交车的乘客平均等待时间:
grouped = sequenced.groupby(['route', 'direction', 'scheduled_interval'])
sims = grouped['actual'].apply(simulate_wait_times)
输出:
route direction scheduled_interval
C northbound 10.0 7.8 +/- 12.5
12.0 7.4 +/- 5.7
15.0 8.8 +/- 6.4
southbound 10.0 6.2 +/- 6.3
12.0 6.8 +/- 5.2
15.0 8.4 +/- 7.3
D northbound 10.0 6.1 +/- 7.1
12.0 6.5 +/- 4.6
15.0 7.9 +/- 5.3
southbound 10.0 6.7 +/- 5.3
12.0 7.5 +/- 5.9
15.0 8.8 +/- 6.5
E northbound 10.0 5.5 +/- 3.7
12.0 6.5 +/- 4.3
15.0 7.9 +/- 4.9
southbound 10.0 6.8 +/- 5.6
12.0 7.3 +/- 5.2
15.0 8.7 +/- 6.0
Name: actual, dtype: object
平均等待时间可能比预期到站间隔的一半长一两分钟,但不是等待时间悖论所暗示的结果。换句话说,这个结果证实了检验悖论,而等待时间悖论似乎与现实不符。
最后的想法
等待时间悖论一直是一个有趣的论题,它涵盖模拟、概率统计假设与现实的比较。虽然我们现在已经确认现实世界的公交线路确实遵循了一些检验悖论,但上述分析也非常明确地表明等待时间悖论背后的核心假设——公交车到站间隔遵循泊松过程有很大问题。
回想起来,这可能并不令人惊讶:泊松过程是一个无记忆过程,它假设公交车到站概率完全独立于自上次到站以来的时间。但在现实中,一个运行良好的公交系统会设计合理的行车时间表,每辆公交车的出发时间都不是随机的,它们要考虑乘客多少。
而由这个问题引出的更大教训,是我们应该谨慎对待任何数据分析任务的假设。虽然泊松过程有时是对到站时间数据的良好描述,但我们不能仅仅因为一种类型的数据看起来和另一种类型的数据很像,就直接想当然地认为对这种数据有效的假设必然对另一种同样有效。看似正确的假设可能导致与现实不符的结论。
原文地址:jakevdp.github.io/blog/2018/09/13/waiting-time-paradox/(附Jupyter Notebook)

星标论智,每天获取最新资讯