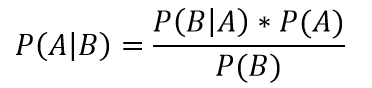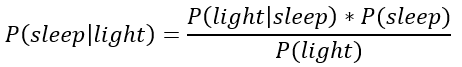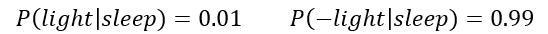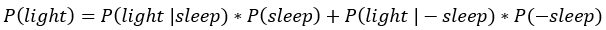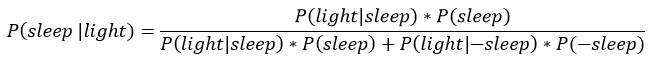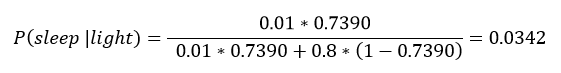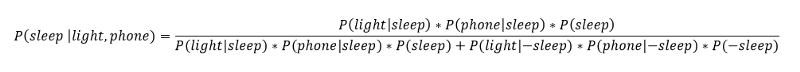“睡觉”还能玩转贝叶斯推断?没错,就连你开不开灯都猜得出来
编译 | 张建军
责编 | 明 明
【导读】贝叶斯法则和其他统计概念很难通过只用到字母的抽象公式、或者一些虚构的情景来理解。在作者William Koehrsen上过的许多课程中,通常会用一些并不是非常有用的例子来展示贝叶斯法则,例如抛硬币或者从缸里抽彩球,但是直到这一个项目才让作者最终理解了如何应用贝叶斯推断。
本文中作者展示了贝叶斯推断通过考虑新的证据来修正我们的信念,从而能更好地模拟真实世界。随着我们收集到更多的证据,我们需要持续调整我们的预测,而贝叶斯公式正好为我们提供了合适的框架。
贝叶斯推断的基本思想是通过更多数据,从而"犯少一点错误"。推断过程很直接:我们首先有一个初始信念,被称为先验,当我们获得额外的信息后可以对这个信念进行修正更新。虽然我们并不知道这个过程就是贝叶斯推断,但是我们一直都在使用这个技巧。
举个例子,我们可能一开始认为我们有百分之五十的可能性会在本季度末升职。如果我们从经理那得到正面的反馈,那么我们就向上调整升职可能性,而相反地,如果我们把咖啡机弄得一团糟,那么我们可能就得降低一下概率了。随着我们不断地获得更多的信息,我们可以不断地修正我们的估计以逼近“正确”的答案。以上我们直觉的行为可以用以下简单却强大的公式来形式化描述,该公式被称为贝叶斯法则(http://www.eecs.qmul.ac.uk/~norman/BBNs/Bayes_rule.htm):
等号左边那项被称为后验,我们读作给定事件B发生后事件A发生的条件概率。在等号右边,P(A)被称为先验,或者被叫作我们对事件A发生的概率的初始信念,P(B|A)被称为似然(也是一个条件概率),这一项是可从数据中得到的,P(B)则是一个归一化常数使得概率分布之和为1。用统计的语言来描述贝叶斯法则的一般形式是后验概率等于似然乘以先验除以归一化常数。这个简短的等式引出了贝叶斯推断的整个领域,也给人们带来了对世界进行推理的有效方法。
虽然等式中的A和B是非常好的占位符,但是它们并不能很好地帮助我们了解如何使用这个概念。为了达到这个目的,可以应用贝叶斯法则去解决一个真实世界的问题。
▌案例
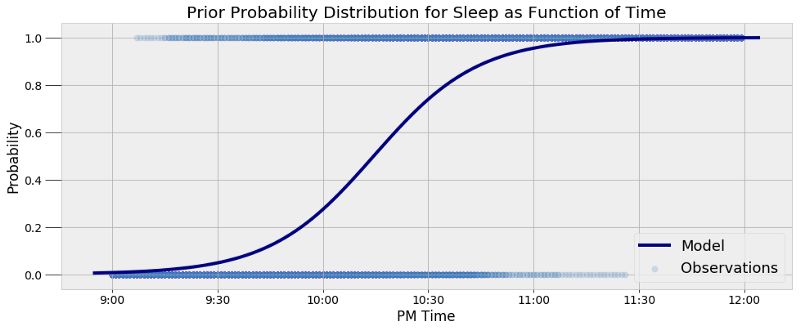
在我自己的生活中,我一直在研究的一个问题就是睡眠模式。我从自己携带的Garmin Vivosmart智能手表中收集了超过两个月的数据,这些数据显示了我何时入睡和起床。在上一篇文章中,我用马尔可夫链蒙特卡罗(Markov Chain Monte Carlo, MCMC)方法计算出了在给定的时间我睡着了的概率。最终模型显示,睡眠的最有可能的分布是一个关于时间的函数(MCMC是一种近似方法),如下图所示。
这是只考虑时间因素的情况下我睡着了的概率。要是我们知道时间的同时还知道其他的证据又会怎样?如果知道我的卧室灯亮着,这会如何改变我睡着了的概率?这就是我们可以利用贝叶斯法则来更新我们的估计的地方了。对于特定时间,如果我们知道我的卧室灯的信息,那么我们可以利用上面的概率分布作为我们的先验,然后应用贝叶斯公式:
等号左边是后验,即给定我的卧室灯的状态(开或关)的情况下我睡着了的条件概率。要是我们没有其他额外的信息可以提供的话,那么在给定时间的睡眠概率将作为我们的先验,P(sleep),或者说作为我们的估计。例如,在晚上10:00,我睡着的先验概率是27.34%。如果我们真的有更多信息,那么我们就可以利用似然来更新这一概率,P(bedroom light |sleep),似然可以从观测数据中得到。根据我的习惯,我知道在我睡着的情况下我的卧室灯亮着的概率是1%。即:
在我睡着的情况下我的灯关掉的概率是1–0.01 = 0.99(这里我用了减号(-)来表示相反的情况)。这是因为条件概率分布之和为1。如果我们知道我睡着了,那么我的卧室灯肯定处于开着或者关着两种情况之一!
等式的最后一项是归一化常数P(light)。这是我的灯开着的全概率。我的灯开着存在两种情况:我睡着了或者我醒着。因此,如果我们知道我睡着了的先验概率,我们可以这样计算归一化常数:
我的灯开着的全概率考虑了两种可能,我睡着了且我的灯开着,以及我醒着且我的灯开着。(P(-sleep) = 1 — P(sleep) 是我醒着的概率)
我醒着的情况下我的灯开着的概率,P(light | — sleep),也是从观测数据中决定的。在我的例子中,我知道如果我醒着,我的卧室灯大概有80%的概率是开着的(这也意味着如果我醒着的话,有20%的可能我的灯是关着的)。
利用我的灯开着的全概率,贝叶斯公式可写成:
这个公式展示了在我的灯开着的情况下我睡着了的概率。如果我的灯灭了,那么我们可以把公式中的P(light|...全部换成P(-light|...
只有文字的公式已经够多了,下面让我们看看怎么利用数字来使用这些公式!
根据公式,我们来一步一步地计算在晚上10:30,我们知道我的卧室灯亮着的情况下,我睡着了的概率是多少。首先,我们根据时间来计算我睡着的先验概率,得到结果是73.90%。这个先验给我们的估计提供了一个很好的起点,但是我们可以通过加入关于我的卧室灯的信息来改善这个估计。既然知道我的卧室灯亮着,我们可以把相关的数字填到贝叶斯公式中去:
卧室灯亮着这一知识很大程度上改变了我们对我睡着了的概率的估计,从70%变成了3.42%。这一变化展示了贝叶斯法则的威力:通过引入更多信息我们可以更新我们的最初估计。虽然我们平时可能根据直觉也会这么做,但是利用正式的公式来思考这一过程可以让我们用一种严谨的方式来更新我们的信念。
让我们尝试另一个例子。假设现在是晚上9:45,且我的卧室灯灭了怎么办?从先验概率是0.1206入手,试试把这个例子解出来。
我不是每次都进行手工推断,而是写了一些Python代码来进行以上的计算,你可以在这个Jupyter Notebook里把玩这些代码。
Jupyter Notebook:https://github.com/WillKoehrsen/ai-projects/blob/master/bayesian_inference/bayes_rule_applied.ipynb
代码输出了以下答案:
Time: 09:45:00 PM Light is OFF.
The prior probability of sleep: 12.06%
The updated probability of sleep: 40.44%
我们再一次发现额外信息改变了我们的估计。现在,如果我的妹妹打算在晚上9:45打电话给我,而且她以某种方法知道我的卧室灯亮着,那么她就可以参照这条等式来判断我是否会接电话了(假设我醒着的时候我总会接电话)!谁说你不能在日常生活中使用统计学的?
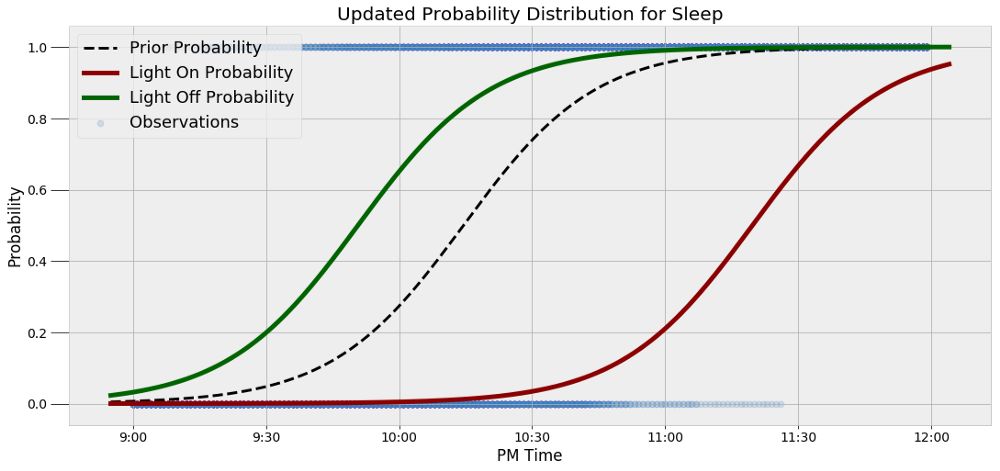
看到数值结果很有帮助,但是数据可视化可以更加清晰地说明问题。在与别人交流想法时,要是他们不能直接通过方程来理解,那么我总是试着引入图像来进行解释。下面,我们可以利用额外的数据来对我睡着了的先验和条件概率分布进行可视化。
当我的卧室灯亮着时,曲线向右进行了移动,意味着在某一特定的时间点我睡着的概率很低。相似地,如果我的灯灭了,曲线向左进行了移动。想从概念上理解一个统计学概念很困难,但是这个插图正好说明了我们为什么要使用贝叶斯法则。如果我们想在这个世界犯少一点错误,那么额外的信息应该改变我们的信念,而贝叶斯推断正是利用一个系统的方法来更新我们的估计。
▌利用更多的证据
为什么要在我的卧室灯这里就止步不前呢?我们可以在模型中使用尽可能多的信息,这个模型也会继续变得更加的精确(只要数据告诉我们相关情况的有用信息)。举个例子,如果我知道在我睡着的情况下,我的手机在充电的似然是95%,那么我们就可以把这个知识加入到我们的模型中。
在这里,我们假设,在给定我是否睡着的信息的情况下,我的手机正在充电的概率条件独立(https://en.wikipedia.org/wiki/Conditional_independence)于我的卧室灯亮着的概率(独立性是一个稍微高级点的概念,但是它可以让我们简化许多问题)。利用额外信息的贝叶斯公式如下表示:
这看上去可能有点吓人,但是利用一点Python代码,我们可以写一个函数来为我们做这些计算。我们输入任意时间,以及灯的开关状态和手机状态这两种状态信息的任意组合,然后这个函数就可以返回更新过的我睡着的概率。
我将跳过数学(我让我的电脑帮我计算)并展示结果:
Time is 11:00:00 PM Light is ON Phone IS NOT charging.
The prior probability of sleep: 95.52%
The updated probability of sleep: 1.74%
在晚上11点,没有额外信息的情况下,我们几乎可以肯定我睡着了。然而,一旦我们有了额外信息:我的灯亮着,手机没有在充电,我们就可以判断我睡着的可能性很低。下面是另一组输入得到的输出结果:
Time is 10:15:00 PM Light is OFF Phone IS charging.
The prior probability of sleep: 50.79%
The updated probability of sleep: 95.10%
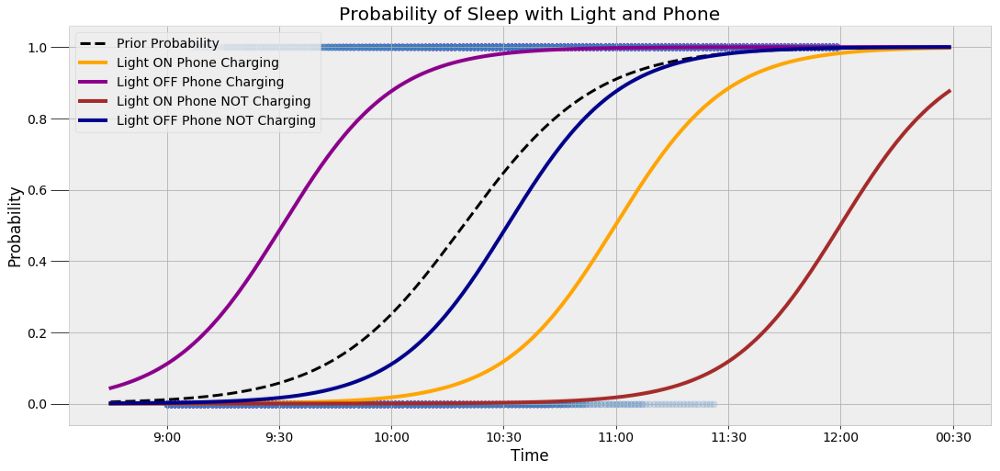
根据具体的情况,概率会变高或变低。为了证明这一点,我们可以观察灯和手机状态的四种不同组合,以及这些组合是如何改变概率分布的:
这幅图包含了许多信息,但是关键点是概率曲线随着证据的不同而发生改变。我们获得更多数据的同时,也可以更好的修正我们的估计。
▌总结
贝叶斯法则和其他统计概念很难通过只用到字母的抽象公式、或者一些虚构的情景来理解。如果你理解一个概念有困难,那么去找出一个你可以应用它的场景,或者看看别人成功应用它的例子!
当我们把概念转化到具体问题时,我们才真正的学到东西。我们不仅可以通过这种方式学到新技能,而且我们还能做一些很酷的项目!成功掌握数据科学需要持续的学习,不断为你的技能添加新技术,并且为不同任务找到最佳的解决方案。
作者 | William Koehrsen
原文链接:
https://towardsdatascience.com/bayes-rule-applied-75965e4482ff
扫描二维码,关注「人工智能头条」
回复“技术路线图”获取 AI 技术人才成长路线图