【速览】TSP 2022 | TS4LRTC:基于可训练子空间的张量缺失成分复原方法
学会“成果速览”系列文章旨在将图像图形领域会议期刊重要成果进行传播,通过短篇文章让读者用母语快速了解相关学术动态,欢迎关注和投稿~
◆ ◆ ◆ ◆
TS4LRTC:基于可训练子空间的张量缺失成分复原方法
*通讯作者:朱策,刘翼鹏
◆ ◆ ◆ ◆
低秩张量补全可以从有限的观测集中恢复在获取、传输、转换等过程丢失的数据项。这使得张量补全在多个应用场景中有推广前景,例如知识图谱获取、交通流量预测、气候数据分析、推荐系统、多任务学习、图像和视频复原等。然而能否成功恢复数据在很大程度上取决于样本复杂度,即成功恢复丢失元素所需的最少观测集。
本文考虑了在辅助数据的帮助下,通过降低样本复杂度,进而提高数据恢复性能,任务模型如图1所示。因此,我们提出了一种基于可训练子空间的张量补全方法TS4LRTC来实现数据复原。具体来说,首先通过字典学习从辅助数据中获取子空间。然后假设待恢复的张量数据由两个低秩成分组成,其中一个成分与辅助数据共享子空间信息,另一个成分在共享子空间之外,来实现利用训练好的子空间信息完成张量补全任务,如图2所示。另外,我们定量分析了子空间信息对样本复杂度的影响,并从理论上给出了子空间信息的有用性。最后,在模拟实验上验证了子空间信息对样本复杂度的影响。基于彩色图像和多光谱图像复原的实验表明,本文所提出的方法在恢复精度和时间复杂度方面优于最先进的方法。
图 1 考虑到辅助数据帮助下的张量补全模型
图 2 可训练子空间的张量补全框架
张量是矩阵的多维扩展,为多维数据提供了自然的表示形式。 探索张量的内部结构可以帮助我们在处理高维数据时获得更多的潜在信息。 例如,多光谱图像(MSI)是三阶张量,通过张量表示,MSI的光谱和空间信息可以同时被索。
数据在采集、传输、转换等过程中,往往会存在缺失项,张量补全可以通过假设待恢复的数据具有低秩的结构信息,进而实现数据的复原。在辅助数据的帮助下,恢复性能会得到进一步提高。现有的大多数方法,包括耦合矩阵张量分解模型和耦合张量秩最小化模型,主要考虑如何提取和利用子空间信息或直接使用辅助数据进行数据补全,其中子空间信息主要指辅助数据和缺失数据的潜在的共享成分。然而, 这些方法要么对给定的秩参数敏感,要么对子空间信息缺乏物理解释。此外,共享子空间信息在当前的张量补全方法中关注较少,尤其是没有分析其对样本复杂度的影响。
因此,关于使用子空间信息进行低秩张量补全,自然会出现以下三个问题:
1. 如何从缺失数据和辅助数据中有效地探索子空间信息?
2. 使用什么样的优化模型才能更好地利用子空间信息实现张量补全?
3. 如何衡量子空间信息对张量补全的影响?
首先,我们简单介绍一下本文中用到的一些符号定义。我们分别用
定义1:模-n积
张量
4.1 模型说明
假设
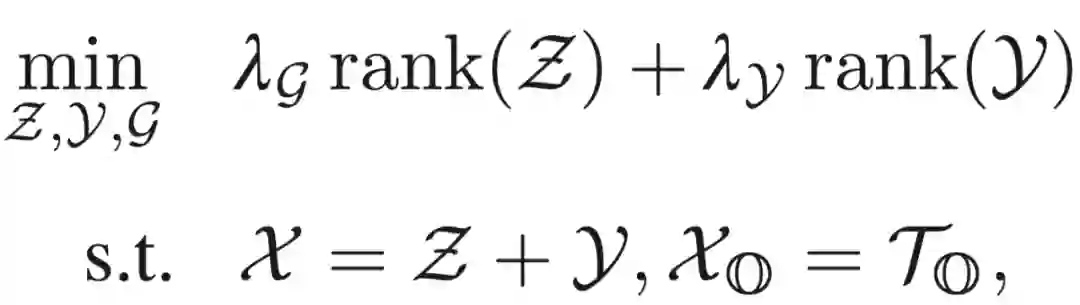
其中

其中
4.2 子空间信息对张量补全模型的影响
我们通过理论分析,得到了所提方法在
5.1 彩色图像数据
为了更直观的看出我们方法的优越性,我们提供了彩色图像复原的结果,其中测试集,结果图分别如图3、图4所示。

图 3 测试集,其中红外图像和深度图像为相应的辅助数据

图 4 在不同的采样率下,不同方法恢复图像的对比结果
5.2 多光谱图像数据
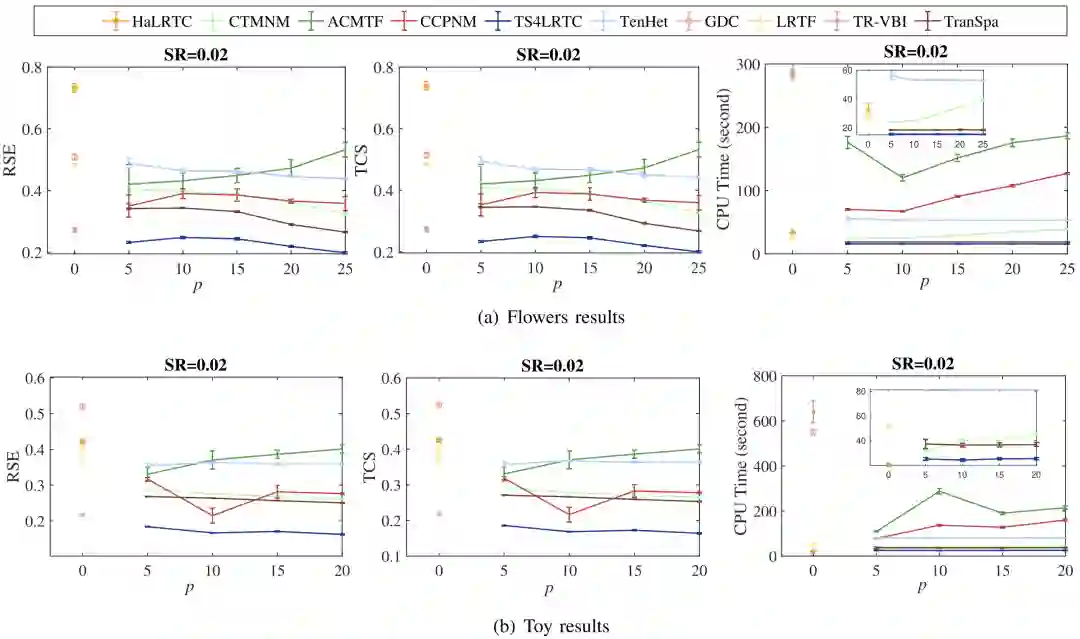
我们采用了大小为512×512×30的多光谱图像数据,其中512×512表示多光谱图像的空间分辨率,30表示多光谱图像的波段数。在这个实验中,我们采取后b个波段作为测试数据,剩下的数据中选取p个波段作为辅助数据,其中
图 5 不同对比方法的恢复性能,其中针对Flowers和Toy多光谱图像,b分别设置成5和10。
图 6 不同对比方法的多光谱图像复原效果,其中b=15,p=15。
我们提出了一种基于可训练子空间的低秩张量补全模型。与当前具有子空间信息的张量补全模型不同,该模型首次考虑了一种数据驱动的方式来学习子空间信息,并在张量补全任务中提供了一种新的利用子空间信息的视角。这个想法也可能对其他张量处理技术有所帮助,例如张量分类、张量鲁棒主成分分析和张量回归。此外,我们给出了所提方法的样本复杂度并从理论上解释了子空间信息的有用性。仿真数据实验表明,子空间信息可以降低张量补全的样本复杂度,尤其在完全共享子空间信息的情况下,样本复杂度降低明显。此外,真实世界数据的实验表明,我们的算法在重构准确性和 CPU 时间方面优于最新算法。
[1] E. Acar, M. Nilsson, and M. Saunders, “A flexible modeling framework for coupled matrix and tensor factorizations,” in Proc. IEEE 22nd Eur. Signal Process. Conf., 2014, pp. 111–115
[2] K. Wimalawarne and H. Mamitsuka, “Efficient convex completion of coupled tensors using coupled nuclear norms,” in Proc. Adv. Neural Inf. Process. Syst., 2018, pp. 6902–6910.
[3] Z. Long, C. Zhu, J. Liu, and Y. Liu, “Bayesian low rank tensor ring for image recovery,” IEEE Trans. Image Process., vol. 30, pp. 3568–3580, 2021.