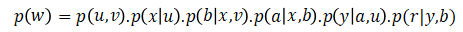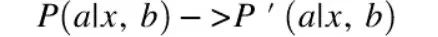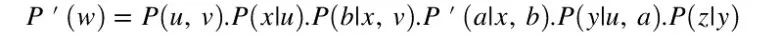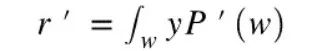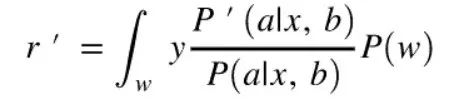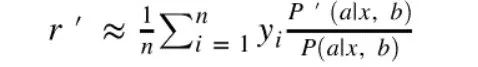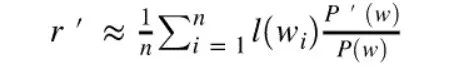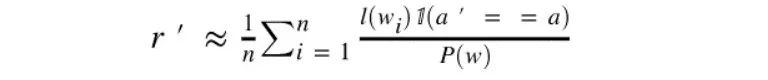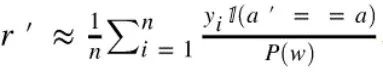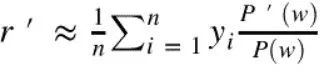如何创建用于离线估算业务指标的测试集？（附代码&链接）

作者：AARSHAY JAIN

翻译：张若楠

校对：张玲

本文约6500字，建议阅读10+分钟

本文将从原理及应用两方面出发，介绍 如何采用日志数据对新模型进行上线测试前的初步筛选评估。

标签：机器学习

简介

 

大多数Kaggle类的机器学习竞赛都没有涵盖机器学习实际工作流程中的一个重点：在构建机器学习产品时搭建离线的评估环境。

比起真正训练机器学习模型，人们通常需要花费更多的努力去清晰地划分训练集/测试集，不断优化某一机器学习指标。在我从事机器学习工程师工作，投入很多时间在监督数据集上训练模型后，我才深有体会。

在这篇博文中，我想介绍设计离线评估环境的一个关键组成部分：创建测试集，该测试集不仅可以用于计算机器学习的基本指标，例如准确率(Accuracy)，精确率(Precision)，召回率(Recall)；还可以估算产品指标，如点击率，收益等。

我们将使用基于反事实评估技术（counterfactual evaluation）的因果推断（causal inference）方法，并使用业界直观的案例来进行解读；然后深入研究Python代码实现，最终模拟出一个真实的场景！

 

目录

 

一、线上与线下进行机器学习模型评估对比

二、广告行业案例研究

三、设计并搭建因果图

四、模型干预

五、使用Python模拟反事实分析（Counterfactual Analysis）

 

一、线上与线下进行机器学习模型评估对比

 

在生产环境中开发和部署机器学习模型，通常从设定基线（baseline）甚至启发式模型开始，也就是使用实时流量进行决策。这样不仅有助于收集数据以训练更复杂的模型，也可以用来作为良好效能的基准。

接下来便是创建训练/验证/测试数据集，并离线训练模型。至此，模型不作任何影响终端用户的决策。建立好模型后，通常的做法是将其在线部署并运行A / B测试，将其与启发式模型进行比较。当对生产中的现有机器学习模型进行迭代时，我们一般也会遵循上述类似的过程。

“在此过程中，最大的挑战之一是如何验证离线模型的有效性，并决定上线测试哪一个模型。”

• 如果离线模型的离线机器学习指标（如AUC）比在线模型更好，那么是否意味着离线模型对业务更有帮助？

• 较高的离线机器学习指标是否意味着业务指标的提升？

• 离线模型的指标需要有多大提升，才值得我们将其部署成新模型或进行A / B测试？

这些是困扰机器学习从业者日常工作的一些常见问题，尤其是在构建面向用户的机器学习产品的时候。这些困扰来自以下3种常见场景：

• 机器学习应用尝试驱动以业务指标（例如点击率，收入，用户参与度等）进行考量的产品，依赖用户在线的反馈/互动，而这些反馈和互动难以离线评估；

• 机器学习模型通常与一些业务策略一起部署，这些策略会影响到模型的输出结果如何去转换为产品动作，例如在进行内容推荐时，同时考虑内容的多样性与用户具体偏好；

• 许多应用程序会接收来自多个模型的预测后进行判断。例如，选择展示哪个广告，可能取决于机器学习模型的点击率和需求预测，同时还要考虑一些业务限制条件，例如广告位的库存和用户匹配性。

在这些情况下，单个模型的常见指标（如准确性，AUC-ROC，精度召回率等）通常不足以判断离线搭建的模型是否比使用中的模型有重大改进。通常可以使用A / B测试进行这种评估，但是在金钱和时间方面，它们的运行成本很高。

在因果推理（Causal Inference）文献的启发下，反事实评估技术（Counterfactual evaluation）提供了一种使用生产日志估算在线指标（如点击率，收入等）的方法。这是很好的中间步骤，有助于筛选离线模型并为A / B测试选择合适的测试对象，从而使我们可以在离线环境中探索更多的模型。

 

二、广告行业案例研究

 

让我们以广告行业为例来更好地理解这一点。考虑以下情形的两方：

• 用户方：用户访问网站并收到广告；如果用户喜欢该广告，则进行点击，反之不会点击；

• 业务方：机器学习系统接收挑选广告的请求，这个请求包含当前用户的上下文信息，而后选择匹配的广告进行展示。

可以使用以下变量定义该系统：

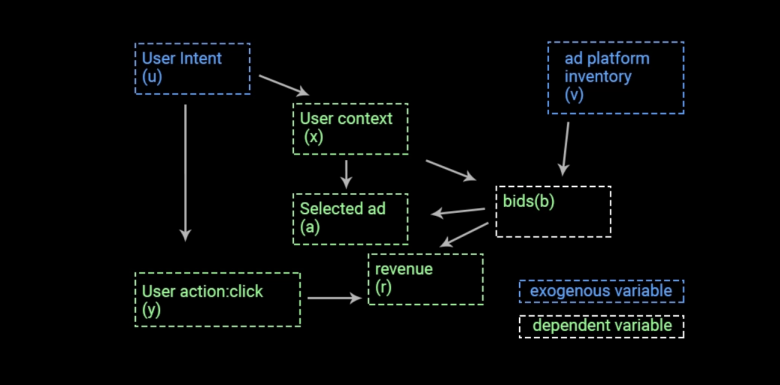
• 用户意图（u）：用户出于某种意图访问网站（例如，用户访问amazon.com购买鞋子）；

• 用户上下文（x）：用户开始在网站上浏览，其浏览行为被打包为上下文内容向量；

• 广告库存（v）：可用于展示的广告位库存量；

• 出价（b）：一种针对广告位每次点击出价的系统；

• 被选广告（a）：根据出价和点击估算值选择的最终广告；

• 用户操作（y）：二进制。如果用户点击了显示的广告则为1，否则为0；

• 收入（r）：用户进行互动后产生的一定形式的收入（$$）。

注意：此处使用的示例和以下数学公式是[1]中使用的示例的略微简化版本（见本文底部链接）。这不是原本研究，而是在尝试通过直观的示例来总结该研究的思想，以及应用在模拟数据上。

 

三、设计并搭建因果图

 

首先，是什么因果图？以下是来自维基百科的定义：

“因果图（也称为路径图，因果贝叶斯网络或DAGs）是用于对数据生成过程的假设进行编码的一种概率图模型。”

上述具有以上变量的系统就可以绘制因果图如下：

从这张图中，我们可以看到不同变量之间的依赖关系或关联关系：

• u, v 是自变量，也叫作“外生变量”

• x = f(u)

• b = f(x, v)

• a = f(x, b)

• y = f(a, u)

• r = f(y, b)

基于这种理解，我们可以将整个系统的联合概率建为一个概率生成模型：

其中w是所有变量的集合。

直观来讲，我们从自变量开始，根据因果图将更多变量链接在一起，并不断将新得到的变量作为接下来的条件变量。请注意，这是一个非循环图，即a可导致b，而从b到a没有反向的因果关系。

 

因果图的隔离假设：

在继续之前，让我们来了解此模型的核心假设之一。像任何因果图一样，该图假设外生变量没有进入关系网的任何后门路径，即外生变量（u，v）与关系网中的其他变量之间不存在共同影响变量。例如，假设存在一个外界因素（e），其将因果图修改为：

在这种情况下，用红色表示的因果路径是后门路径，这会使先前定义的公式组无效。表示此假设的另一种方式是：我们假设所有外生变量的观察值都是从未知但固定的联合分布中独立采样的。这就是隔离假设（Isolation Assumption）。

大多数因果图都会采取这个假设。由于并非所有预期的影响因素都可以估值/建模，我们应该尝试估值最有影响力的事件。在分析结果时要牢记这一假设，这很关键。

 

四、模型干预

 

因果图和方程组允许我们更改图中的单个元素，并估计此对下游事件所定义的指标的影响。

“假设点击率是我们试图最大化的业务指标。点击率定义为用户在整个用户会话中点击的广告所占的比例。假设我们正在运行一个上线系统，现在我们开发了一个用于选择广告的新模型，即我们有了一种得到变量a的新方法。我们要估算该新模型的点击率，作为当前在线模型的比较。”

该方程组使我们能够将模型的干预视作一种代数计算，也就是我们可以更改一些中间分布，从而能够为给定的输入输出不同的结果。

 

反事实分析——评估一个假设模型的部署：

现在，让我们深入了解反事实分析原理，并尝试解决上述问题。

 

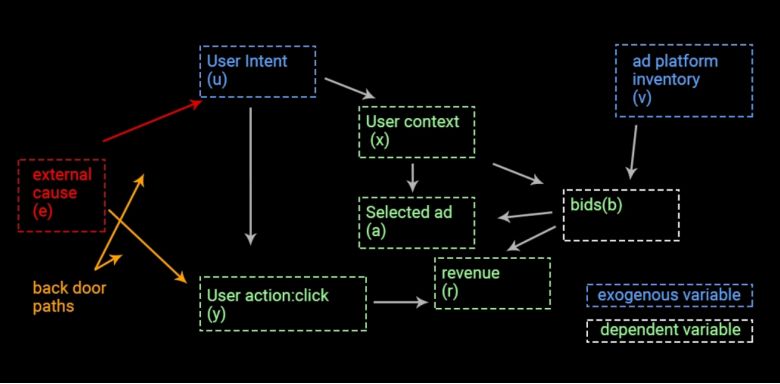
• 什么是反事实分析？

如果我们用新的模型M'替换当前的模型M会发生什么情况？-- 这个问题就是反事实，因为我们实际上并没有做出改变，且不会影响用户体验。假设我们要部署模型M’，我们只是试图估计这个场景中的业务指标。

 

• 类比传统机器学习

让我们尝试将这种场景与传统的有监督学习进行比较。

在有监督学习环境中训练模型时，我们使用一些自变量x和实际值y，然后尝试将y估计为y’= f(x)。y’是一种假想的估计，也就是如果使用模型f(x)而不是系统来生成数据将会发生的情况。

然后我们定义损失函数并优化模型。这些都能奏效是因为f(x)是被完全定义好的，而在我们的问题中情况并非如此（没有办法知道如果显示不同的广告，用户将如何进行交互）。因此我们需要一些解决方法，以便我们可以在不完全定义系统的每个成分的情况下仍能够估算指标。

 

• 马尔可夫因子置换作用于反事实分析

接下来，让我们尝试在方程组中执行代数运算。假设我们有一个新模型M’来选择已给出定价的广告。这只会影响方程式的一个组成部分：

新的联合分布成为：

 

请注意，只有一个分布在此被更改。这个系统中的点击率可以定义为每次广告展示的点击期望值：

直观来讲，这可以理解为在不同的上下文动作场景中发生的点击次数的平均值，用w表示（译者注：此处作者想表达的应该是r），由w的概率分布加权，如上文所述w是关于用户行为和线上模型M的函数。

对于新模型M’，点击率将为：

要分析新模型M'的点击率，我们可以假定用户行为输入不变，简单的使用新模型M'来调整概率分布。可以重写为：

 

这里假设积分中分母项在w的值域内大于零。根据大数定律，我们可以将r’近似为：

 

请观察我们如何在最终估计中消除了系统中的大多数成分。这非常有力，因为现在我们不需要为新模型M'去完整构建这一联合分布P’(w)，而只需确定产生变化和受到了影响的部分。而由于模型干预是受控制的，上述的内容便很容易确定。

这个想法可以推广到任何给定的指标l(w)，基于概率分布P’(w)，使用离线模型M’得到反事实估计。这一推广可以使用具有概率分布P(w)的日志数据计算为：

• Marko因子替换的启发

让我们尝试通过一个小例子来理解这个概念。假设有5个数据点：

浏览内容	p(M)	y	p(M’)
w1	0.8	1	0.3
w2	0.6	1	0.5
w3	0.2	0	0.4
w4	0.1	0	0.3
w5	0.7	1	0.6

在此：

• 每行数据表示一个显示广告的浏览内容上下文；

• P(M)是采用线上模型M的日志中展示广告的概率；

• P(M’)是采用离线模型M’展示了相同广告的概率；

• y是用户操作，如果点击则为1，否则为0。

我们可以看到，线上模型普遍在用户有单击条件下展示广告概率更高，因此它是一个更好的模型，采用我们上文的估计量也会得出类似的推论。因此，我们能够用反事实估计值对模型进行直观的排序。

 

• 约束条件以及可实践性的考量

如果我们仔细观察最终方程，它对要评估的模型施加了约束条件。这个新模型本质上必须是一个概率模型，我们能够计算其产生与日志中模型完全相同决策的概率，这可能并不总是一个微小的概率。

假设我们只拥有新模型在输入日志数据后得到的最终广告选择决策a’，我们可以从基于倾向得分匹配的方法[2]中获取灵感，重新编写这一方程式如下：

直观来讲，你可以将其理解为把新模型视为概率模型，当新模型对某一行日志数据采取了与日志模型不同的决策时，在该处视其概率分布P’(w) = 0。

实际上，如果我们新模型的决策数量较少，并且我们期望从日志数据中匹配到很多决策，那么使用以上匹配方法是可行的。但是，在很多情况下（例如推荐算法，信息检索或多臂老虎机问题），我们可能没有足够的数据来获得足够的匹配以进行可靠的估计，从而导致估计量具有高方差。

为简单起见，我们将不在本文中讨论如何考虑方差，但读者可以随时在本文底部提供的参考文献[1] [2]中阅读更多内容。

 

五、使用Python模拟反事实分析

 

至此，你已经对反事实分析有了一些直观和数学的理解。让我们使用一个模拟的示例，与我们正在研究的示例类似，进一步进行操作。假设：

• 我们的清单中有3个广告，对所有用户均有效；

• 我们模拟了N个用户浏览上下文，即N个不同的用户场景。每个用户场景对每个广告有相互独立的点击概率；

• 我们通过在不同情况下向用户随机投放广告并观察点击行为来收集一些在线数据。随机投放是收集公正的在线数据以评估在线模型的好方法，应尽可能采用这一方法。

1. 数据准备

让我们模拟一些记录的数据，这些数据类似于生产系统中的数据。让我们先导入必要的程序包。

import numpy as npimport pandas as pdimport matplotlib.pylab as pltfrom uuid import uuid4%matplotlib inline

 

• 用户阅览内容

我们先定义10,000个用户阅览内容(x) 的ID，然后定义它们发生的概率分布，即某些内容比其他内容更有可能重复出现。

# set user contextsnum_contexts = 10000user_contexts = np.asarray(["context_{}".format(i) for i in range(num_contexts)])
# assign selection prior to these contextsdef random_normal_sample_sum_to_1(size):    sample = np.random.normal(0, 1, size)    sample_adjusted = sample - sample.min()    return sample_adjusted / sample_adjusted.sum()user_context_selection_prior = random_normal_sample_sum_to_1(num_contexts)plt.hist(user_context_selection_prior, bins=100)assert user_context_selection_prior.sum().round(2) == 1.0

 

• 不同内容下点击概率

让我们在库存中定义3个广告。为了简单起见，假设在给定内容中某个广告的点击率可以是以下之一：

• 低：10％

• 中：40％

• 高：60％

然后，我们可以随机分配哪个广告在哪种情况下属于低/中/高频率。这样做的想法是，一个良好的模型会给定的阅览内容背景中更频繁地选择展示容易产生互动的广告，而不是低互动广告。

2. 随机数据集

现在，让我们模拟100,000次迭代，每次随机取10,000个用户阅览信息中的1条作为模型的输入，并投放一个随机的广告。随后我们根据该阅览信息中该广告的先验概率，对点击或不点击的行为进行随机生成。

这里的想法是生成任意模型生产日志的相似数据，不同之处在于我们模拟的是用户端行为。

模拟出的数据将包含四列：

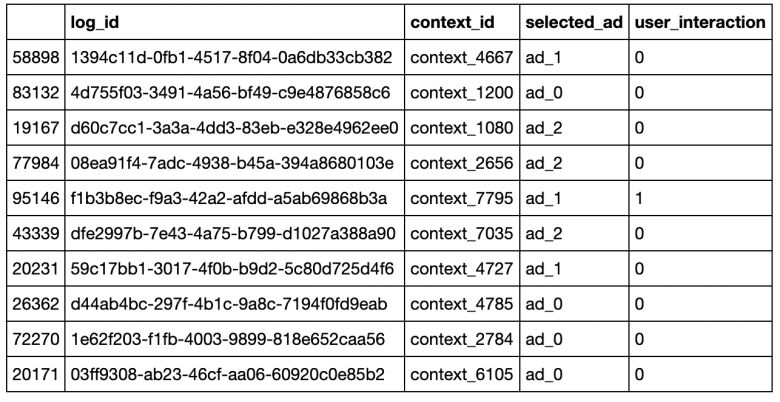
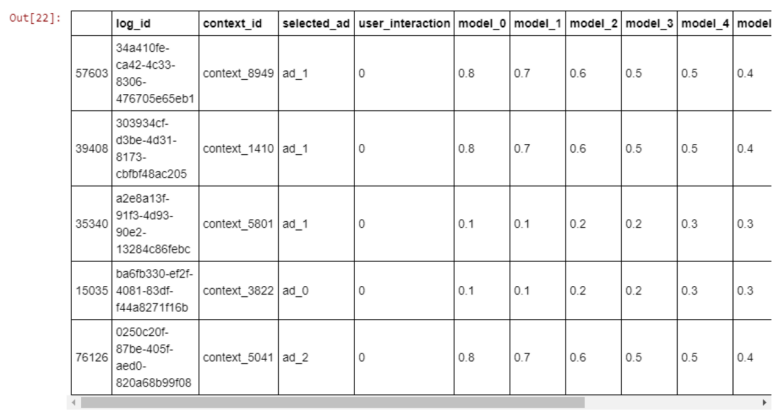
• log_id：代表记录的每一行；

• context_id：代表我们从10,000个内容列表中抽取的1个内容id；

• selected_ad：线上模型显示的广告；

• user_interaction：二进制，如果用户进行了交互，则为1；否则为0。

num_iterations = 100000
# create empty df for storing logsdf_random_serving = pd.DataFrame(    columns = ["log_id", "context_id", "selected_ad", "user_interaction"])
# create unique ID for each log entrydf_random_serving["log_id"] = [uuid4() for _ in range(num_iterations)]
# assign a context id to each log entrydf_random_serving["context_id"] = np.random.choice(user_contexts, size=num_iterations, replace=True, p=user_context_selection_prior)
# randomly sample an ad to show in that contextdf_random_serving["selected_ad"] = np.random.choice(ads, size=num_iterations, replace=True)
# for each log entry, sample an action or click or not using the click probability assigned to the context-ad pair in step 1def sample_action_for_ad(context_id, ad_id):    prior = user_context_priors.get(context_id)[np.where(ads == ad_id)[0][0]]    return np.random.binomial(1, prior)df_random_serving["user_interaction"] = df_random_serving.apply(lambda x: sample_action_for_ad(x["context_id"], x["selected_ad"]), axis=1)
# a snapshot of the datadf_random_serving.sample(10)

回顾一下，此模拟日志数据中的每一行都代表一个实例，其中：

• 用户出于某种意图访问了网站，并生成了由context_id表示的用户浏览内容（x）；

• 线上模型（在这种情况下为随机选择模型）选择了要展示给用户的广告；

• 观察并记录了用户行为。

3. 新模型评估

• 定义新模型

接下来，让我们定义一些模型，我们需要能够直观地知道这些模型点击率的效果排名。这将使我们能够模拟离线模型预测，使用反事实估计来获取指标，并将其与预期的结果进行比较。

一种方法是用向量 [p_low, p_med, p_high] 对给定浏览内容表示低/中/高的不同先验概率。我们可以凭直觉说，对该情景而言更倾向于选择更高互动广告的模型会更好。请注意，这不是实际模型的工作方式，因为模型事先不知道点击率；可以将它们视为对这些先验概率有着不同估计准确率的既有模型。

这里是10个模型，它们的预期效果逐渐升高：

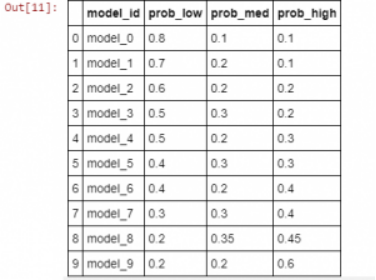
new_model_priors = np.atleast_2d([    [0.8, 0.1, 0.1],    [0.7, 0.2, 0.1],    [0.6, 0.2, 0.2],    [0.5, 0.3, 0.2],    [0.5, 0.2, 0.3],    [0.4, 0.3, 0.3],    [0.4, 0.2, 0.4],    [0.3, 0.3, 0.4],    [0.2, 0.35, 0.45],    [0.2, 0.2, 0.6]])

为了更加明确，我们将其转为DataFrame：

new_model_names = np.asarray(["model_{}".format(i) for i in range(new_model_priors.shape[0])])pd.DataFrame(    data=np.hstack([np.atleast_2d(new_model_names).T, new_model_priors]),    columns=["model_id", "prob_low", "prob_med", "prob_high"])

以这种方式定义模型的一个好处是，我们实际上可以计算出每个模型的期望点击率。由于模型的本质就是用来选择低/中/高频广告的一组概率，并且我们已经定义好了了低/中/高频广告的点击率，因此我们可以直接用点乘来估算每个模型下的点击率：

# expected interaction rate:expected_interaction_rates = np.dot(new_model_priors, np.atleast_2d(ad_interaction_priors).T)expected_interaction_rates.ravel()
# Output: array([0.17 , 0.19 , 0.24 , 0.26 , 0.29 , 0.31 , 0.34 , 0.36 , 0.395, 0.44 ])

我们可以看到期望点击率就是我们预期的顺序。现在，我们将尝试使用每种政策对广告选择进行抽样，并使用上面学到的反事实技术来查看是否可以仅使用每个模型的记录数据和抽样结果来估算这些点击率。

 

• 估算点击率：倾向得分匹配

首先，让我们使用倾向匹配估算值：

其中：

• yi：用户行为；

• a’：新模型产生的决策；

• a：线上模型产生的决策；

• P(a|x,b)：线上模型在日志中的选择展示某广告的概率（注意线上模型是随机选择的）。

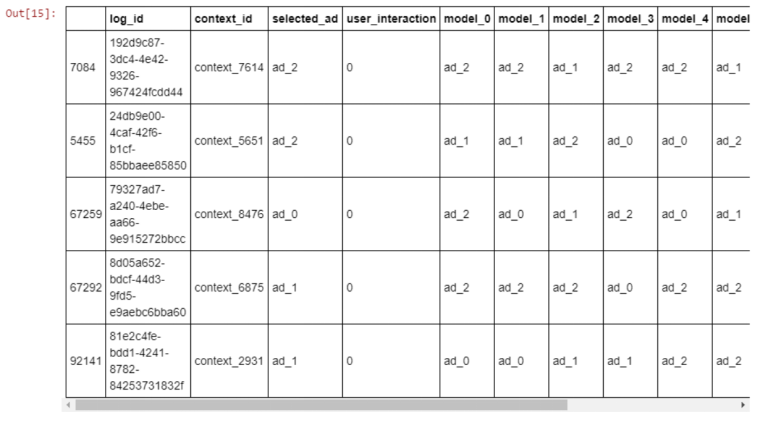
# use the same context ids as logged data:df_new_models_matching = df_random_serving.copy()
def sample_ad_for_context_n_model(context_id, model_priors):    # get ad interaction priors for the given context    interaction_priors = user_context_priors.get(context_id)
    # get the selection prior for the given model based on interaction priors    selection_priors = model_priors[np.argsort(np.argsort(interaction_priors))]
    # select an ad using the priors and log the selection probability    selected_ad = np.random.choice(ads, None, replace=False, p=selection_priors)#     selected_ad_prior = selection_priors[ads.tolist().index(selected_ad)]    return selected_ad
for policy_name, model_prior in zip(new_model_names, new_model_priors):    df_new_models_matching.loc[:, policy_name] = df_new_models_matching["context_id"].apply(lambda x: sample_ad_for_context_n_model(x, model_prior))
df_new_models_matching.sample(5)

我们可以看到，对于每个日志条目，我们都从所有新模型中计算出广告选择。

# match and estimate:estimates_matching = []for i in range(len(new_model_names)):    model = "model_{}".format(i)    matching_mask = (df_new_models_matching["selected_ad"] == df_new_models_matching[model].values).astype(int)
    # the logging policy was random so we know P(w) = 1/3    estimate = (df_new_models_matching["user_interaction"] * matching_mask / 0.333).sum() / df_new_models_matching.shape[0]    estimates_matching.append(estimate)

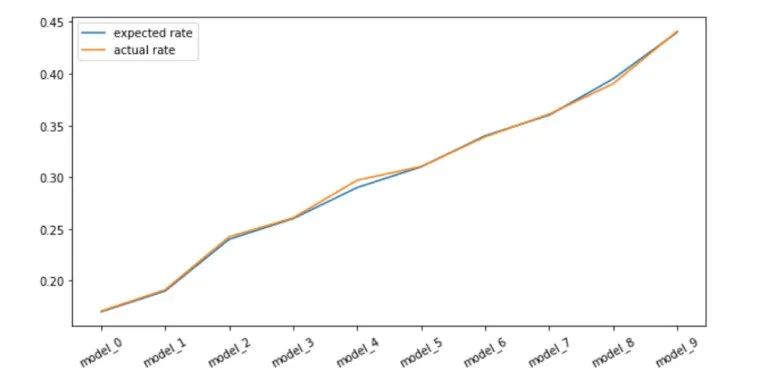
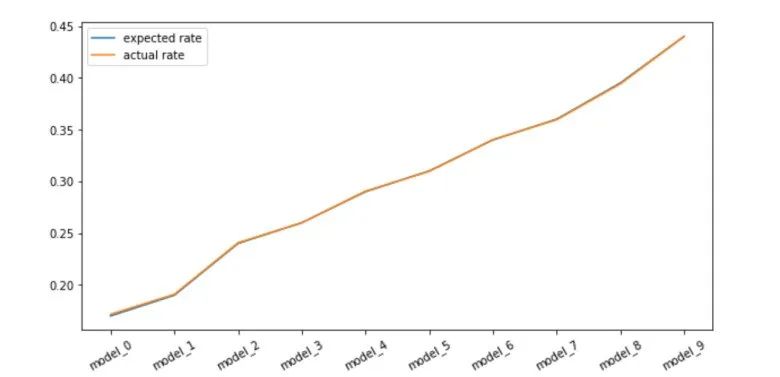
plt.figure(figsize=(10,5))plt.plot(expected_interaction_rates, label="expected rate")plt.xticks(range(10), labels=new_model_names, rotation=30)plt.plot(estimates_matching         , label="actual rate")plt.legend()plt.show()

• 估算点击率：倾向得分加权
  

首先，让我们使用倾向匹配估算值：

其中：

• yi：用户行为；

• P’(a | x, b)：评估离线模型的选择概率；

• P’(a | x, b)：生产模型的日志概率（随机投放）。

# use the same context ids as logged data:df_new_models_weighting = df_random_serving.copy()
def sample_prior_for_context_n_model(context_id, model_priors, selected_ad):    # get ad interaction priors for the given context    interaction_priors = user_context_priors.get(context_id)
    # get the selection prior for the given model based on interaction priors    selection_priors = model_priors[np.argsort(np.argsort(interaction_priors))]
    # get prior of the selected ad    selected_ad_prior = selection_priors[ads.tolist().index(selected_ad)]    return selected_ad_prior
for model_name, model_prior in zip(new_model_names, new_model_priors):    df_new_models_weighting.loc[:, model_name] = df_new_models_weighting.apply(lambda x: sample_prior_for_context_n_model(x["context_id"], model_prior, x["selected_ad"]), axis=1)
df_new_models_weighting.sample(5)

我们可以看到，对于每个日志条目，我们已经对所有新模型计算了该模型与在线模型采取相同的广告展示的概率。

# match and estimate:estimates_weighting = []for i in range(len(new_model_names)):    model = "model_{}".format(i)
    # the logging policy was random so we know P(w) = 1/3    estimate = (df_new_models_weighting["user_interaction"] * df_new_models_weighting[model] / 0.333).sum() / df_new_models_weighting.shape[0]    estimates_weighting.append(estimate)

plt.figure(figsize=(10,5))plt.plot(expected_interaction_rates, label="expected rate")plt.xticks(range(10), labels=new_model_names, rotation=30)plt.plot(estimates_weighting, label="actual rate")plt.legend()plt.show()

总结

 

我们可以看到，在两个估计量中，我们都能够估计每个模型的正确的被点击率。换句话说，如果我们不能事先知道每个模型上线后的实际表现将会有怎样的名次，那么该技术将帮助我们仅从每个模型对日志数据的预测结果中选择更适合的模型。

值得注意的是，在这模拟案例中，我们能够获取准确的点击率。但实际上可能存在各种产生干扰的因素，导致我们无法获得确切的数字。然而在考量离线评估方法时，我们始终可以遵循三个规则，按重要性排序：

1. 方向性： 如果模型A的在线指标>模型B，则模型A的反事实指标>模型B。

2. 变化率： 如果模型A的在线指标比模型B多10％，则反事实指标也要高出相似的数量。

3. 确切值： 如我们的示例所示，在线指标和反事实指标的绝对值非常接近（这是理想情况）。

你觉得这有用吗？你能想到在日常工作中该技术可能有用的情况吗？您是否看到文章没有考虑到此方法的某些限制？请留下带有反馈/批评/问题的评论， 我希望能够进行更多的讨论。

 

参考书目/延伸阅读

本文主要受到[1]和[2]的启发。如果您有兴趣进一步研究，[3] [4] [5]是有趣的读物，具有更多类似上下文的应用程序：

[1]. Counterfactual Reasoning & Learning Systems

https://arxiv.org/abs/1209.2355

[2]. Counterfactual Estimation and Optimization of Click Metrics for Search Engines

https://arxiv.org/abs/1403.1891

[3]. The Self-Normalized Estimator for Counterfactual Learning

https://papers.nips.cc/paper/5748-the-self-normalized-estimator-for-counterfactual-learning

[4]. Unbiased Offline Evaluation of Contextual-bandit-based News Article Recommendation Algorithms

https://arxiv.org/abs/1003.5956

[5]. Off-policy evaluation for slate recommendation

https://arxiv.org/abs/1605.04812

 

原文标题：

How to Create a Test Set to Approximate Business Metrics Offline

原文链接：

https://www.analyticsvidhya.com/blog/2020/02/how-to-create-test-set-approximate-business-metrics-offline/

编辑：黄继彦

校对：林亦霖

译者简介

张若楠，UIUC统计研究生毕业，南加州传媒行业data scientist。曾实习于国内外商业银行，互联网，零售行业以及食品公司，喜欢接触不同领域的数据分析与应用案例，对数据科学产品研发有很大热情。

——END——