有限元碰撞,实现前所未有的精确、稳定、无穿透仿真效果 | SIGGRAPH 2020
编辑 | 丛 末
碰撞的严谨定义
 在每个时间歩可通过最小化Incremental Potential
在每个时间歩可通过最小化Incremental Potential
 来更新:(使用隐式欧拉时间积分)
来更新:(使用隐式欧拉时间积分)

 ,其中
,其中
 为采样点速度,
为采样点速度,
 为外力(比如重力),
为外力(比如重力),
 为采样点的质量矩阵,
为采样点的质量矩阵,
 为时间歩长。
为时间歩长。
 是弹性势能。最小化Incremental Potential是一个已经解决的很好的问题,用牛顿迭代辅助line search就能保证稳定、精确地求解。但如果考虑碰撞呢?其实也很简单:
是弹性势能。最小化Incremental Potential是一个已经解决的很好的问题,用牛顿迭代辅助line search就能保证稳定、精确地求解。但如果考虑碰撞呢?其实也很简单:

-
第 k 个“点 -三角
”对:

-
第 k 个“边 -边
”对:


局部障碍函数
 和
和
 其实都可以根据相对位置关系写成连续分段解析函数,我们对“无穿透”三个字的数学描述还是很昂贵的:a 可以取0到1之间无穷个实数,k 的个数则是物体表面点、边、三角形数量的二次方级别的!而IPC的解决方案,就是巧用连续碰撞检测(CCD)来对付a,并构造光滑的局部障碍函数来对 k 降维!
其实都可以根据相对位置关系写成连续分段解析函数,我们对“无穿透”三个字的数学描述还是很昂贵的:a 可以取0到1之间无穷个实数,k 的个数则是物体表面点、边、三角形数量的二次方级别的!而IPC的解决方案,就是巧用连续碰撞检测(CCD)来对付a,并构造光滑的局部障碍函数来对 k 降维!
 线性渐变成
线性渐变成
 ,那么只要我们在这两个状态间做CCD,找出第一次恰好产生穿透的那个 a,然后保证这一步迭代的更新步长不超过这个找出的 a 就好了,而无需对迭代更新过程进行更多的采样。(注意这里说的是迭代步长而不是时间步长。)这其实是一种line search filtering,常在内点法中使用。
,那么只要我们在这两个状态间做CCD,找出第一次恰好产生穿透的那个 a,然后保证这一步迭代的更新步长不超过这个找出的 a 就好了,而无需对迭代更新过程进行更多的采样。(注意这里说的是迭代步长而不是时间步长。)这其实是一种line search filtering,常在内点法中使用。

 是接触硬度,在IPC中通过数值分析自动调节。
是接触硬度,在IPC中通过数值分析自动调节。

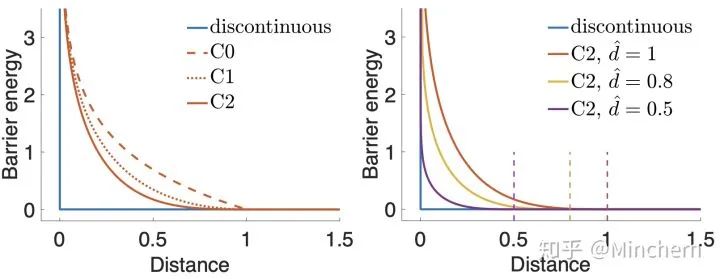
 就是IPC接触力产生的临界距离,一般设成毫米至微米级别。注意我们的函数 b 在
就是IPC接触力产生的临界距离,一般设成毫米至微米级别。注意我们的函数 b 在
 处也是C2连续的,画出来就是下图中的C2曲线:
处也是C2连续的,画出来就是下图中的C2曲线:
 设置的越小,IPC对真实碰撞模型的近似也就会越精确,需要在优化中计算的接触力和力贾科比矩阵的接触元对也越少,配合空间哈希快速找出需要考虑的接触元对,就能实现高效的仿真了!
设置的越小,IPC对真实碰撞模型的近似也就会越精确,需要在优化中计算的接触力和力贾科比矩阵的接触元对也越少,配合空间哈希快速找出需要考虑的接触元对,就能实现高效的仿真了!
摩擦力
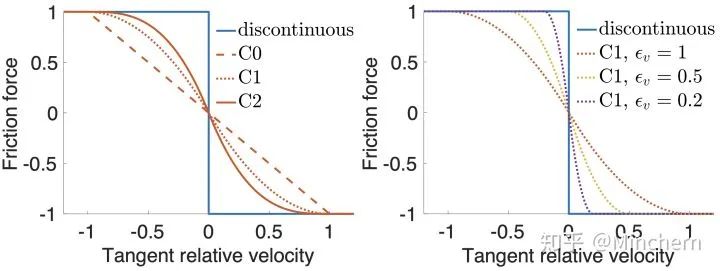
 内,从而构造出了近似的摩擦力势能,并融合到Incremental Potential中,实现了完整的Incremental Potential Contact:
内,从而构造出了近似的摩擦力势能,并融合到Incremental Potential中,实现了完整的Incremental Potential Contact:

 是所有上一个时间歩中的法向接触力不为0的接触元对,
是所有上一个时间歩中的法向接触力不为0的接触元对,
 和
和
 是它们在上一个时间歩中的法向接触力和切平面算子,
是它们在上一个时间歩中的法向接触力和切平面算子,
 是近似摩擦势能(
是近似摩擦势能(
 为近似摩擦力)。更多细节见原文。
为近似摩擦力)。更多细节见原文。
精度验证
 都是resolution independent,所以refine后随着接触元对数量增加,结果肯定是不收敛的,这点我们在对IPC的后续研究中也发现了,并会有所改进。至于其它力,我们为了效率直接使用的是线性微元和lumped mass matrix,收敛性和能量守恒当然也是一般了,而且在大形变中肯定也有locking,这都是我们没有关注的点,而且后者和IPC关注的有限元碰撞也算是相对独立。
都是resolution independent,所以refine后随着接触元对数量增加,结果肯定是不收敛的,这点我们在对IPC的后续研究中也发现了,并会有所改进。至于其它力,我们为了效率直接使用的是线性微元和lumped mass matrix,收敛性和能量守恒当然也是一般了,而且在大形变中肯定也有locking,这都是我们没有关注的点,而且后者和IPC关注的有限元碰撞也算是相对独立。
开源项目
https://github.com/ipc-sim/IPC/wiki
shapes input 2
input/tetMeshes/cube.msh 0 3 0 0 0 0 1 1 1
input/tetMeshes/cube.msh 0 1 0 0 0 0 1 1 1
selfFric 0.1
ground 0.1 0
shapes input 2
input/tetMeshes/cube.msh 0 3 0 0 0 0 1 1 1 material 3000 1e8 0.4
input/tetMeshes/cube.msh 0 1 0 0 0 0 1 1 1
selfFric 0.1
ground 0.1 0
shapes input 2
input/tetMeshes/cube.msh 0 3 0 0 0 0 1 1 1
input/tetMeshes/cube.msh 0 1 0 0 0 0 1 1 1 DBC -0.1 -0.1 -0.1 0.1 1.1 0.1 -0.2 0 -0.2 0 0 0 DBC 0.9 -0.1 0.9 1.1 1.1 1.1 0.2 0 0.2 0 0 0
selfFric 0.1
ground 0.1 0
shapes input 2
input/tetMeshes/cube.msh 0 3 0 0 0 0 1 1 1
input/triMeshes/triangle.seg 0 1 0 0 0 0 2 2 2 angularVelocity 10 90 0
selfFric 0.1
ground 0.1 0
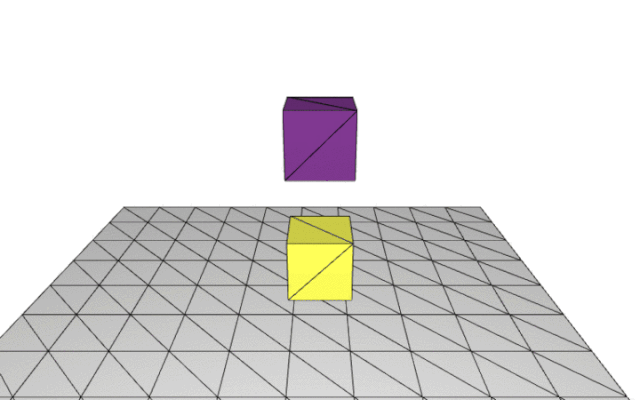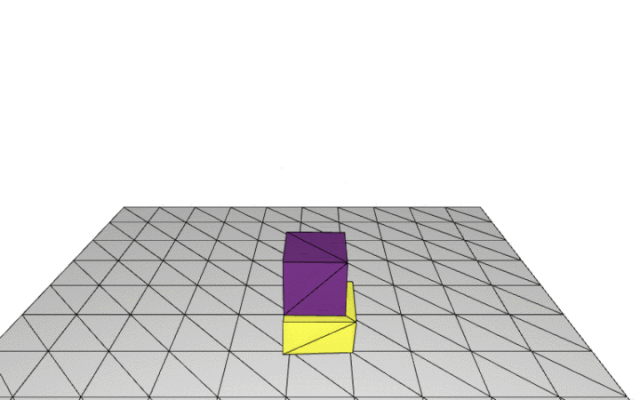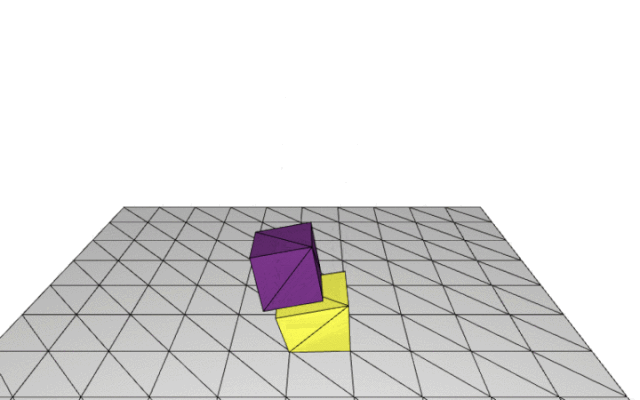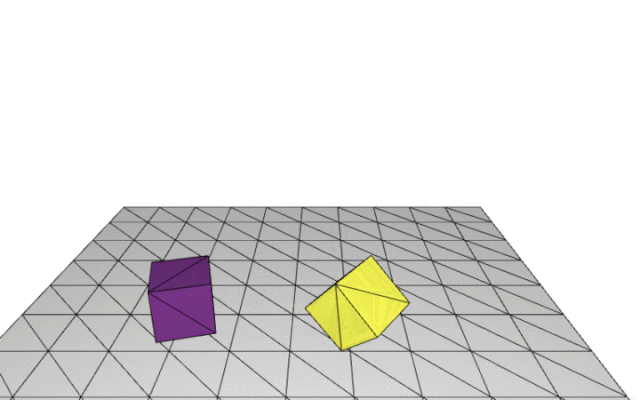
zoom 0.3
IPC开源项目hello world仿真场景变种 —— 正方体与预设三角线框的contact
AI 科技评论希望能够招聘 科技编辑/记者
办公地点:北京/深圳
职务:以跟踪学术热点、人物专访为主
工作内容:
1、关注学术领域热点事件,并及时跟踪报道;
2、采访人工智能领域学者或研发人员;
3、参加各种人工智能学术会议,并做会议内容报道。
要求:
1、热爱人工智能学术研究内容,擅长与学者或企业工程人员打交道;
2、有一定的理工科背景,对人工智能技术有所了解者更佳;
3、英语能力强(工作内容涉及大量英文资料);
4、学习能力强,对人工智能前沿技术有一定的了解,并能够逐渐形成自己的观点。

登录查看更多
相关内容
专知会员服务
12+阅读 · 2020年1月3日
Arxiv
4+阅读 · 2018年5月9日