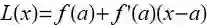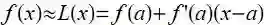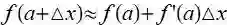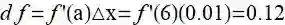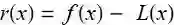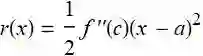【最优化和线性化】图解普林斯顿微积分 11

第13 章最优化和线性化

13.1 最优化(Optimization)

13.1.1 一个简单的最优化例子

涉及最优化时, 通常我们关心的是全局最大值和最小值.

13.1.2 最优化问题：一般方法

13.1.3 一个最优化的例子

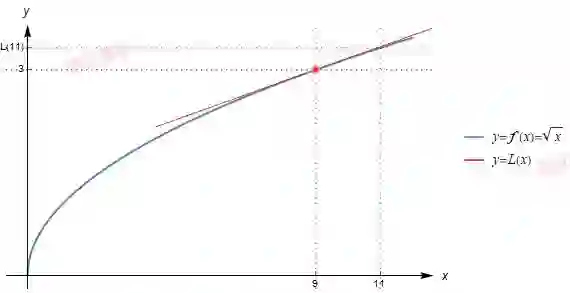
假设只有300 英尺长的篱笆可供使用, 并且农场主想要围成一个直角三角形的农场, 并且使新圈出的地的面积(下图绿色三角形区域)尽可能地大. 那么这块地的周长和面积分别为多少？

(1) 首先要识别出一些变量. 设三角形的底边为 b, 高为 h, 斜边为H, 并且面积 A. 限制条件篱笆的长度 h+H, 目标最大化 A;(2) 由题意可知 0<=b<=300, 0<=H<=300, 0<=h<=150;(3) 列出方程组 A=bh/2, h+H=300, $b^2+h^2=H^2$;(4) 消去 b 和 H 得到 $\text{A=5h}\sqrt{900-6h}$;(5) 求导 $\frac{dA}{dh}=\frac{45(100-h)}{\sqrt{900-6h}}$(6) 求得 h=100 时候, A = $5000\sqrt{3}$, 并进行验证(7) 得到结论.

13.2 线性化(Linearization)

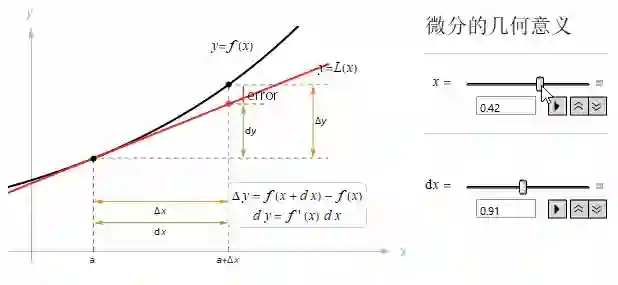
使用导数去估算特定的量. 例如想要估计 $\sqrt{11}$ 的值. 设 $\text{f(x)=}\sqrt{x}\text{, x}\ge \text{0}$ , 并且绘制出通过点 (9,3) 的切线, 记为 y=L(x).

观察图形可以看到在 x=9 附近 L(x)非常接近于曲线 y=f(x) , 这意味着切线 L(11) 是对 $\text{f(11)=}\sqrt{11}$很好的近似.

现在来计算出 L(11). 线性函数 L(x) 通过点(9,3), 并且它与曲线 f(x) 在 x=9 处相切, 所以 L(x) 的斜率为 f'(9)=1/6, 于是方程为 $\text{y-3=}\frac{1}{6}\text{(x-9)}$ , 将 11 带入可得到结论 $\sqrt{11}\approx \text{3}\frac{1}{3}$

13.2.1 线性化问题：一般方法

如果想要估算某个量, 首先试着把它写成某个适当的函数 f(x) 的值. 在上述例子中, 我们想要估算 $\sqrt{11}$, 就设函数 $\text{f(x)=}\sqrt{x}$.

接下来, 我们选某个与 x 很接近的数 a, 并使得 f(a) 容易计算.

再次, 已知函数 f 和特殊值 a, 我们找出通过曲线 y = f(x) 上点(a, f(a)) 的切线. 这条切线的斜率为 f'(a), 其方程为 y-f(a)=f'(a)(x-a), 如果设切线为 y=*L*(x), 则

这个线性函数L 被称为 f 在 x = a 处的线性化:

13.2.2 微分(The differential)

定义 △x=x-a , 将上面公式变为

量df 被称为 f 在 x=a 处的微分, 它是当 x 从 a 变化为 a+△x 时 f 的变化量的近似. 这意味着 x 的微小变化会引起 y 的变化, 而后者的变化量约为前者的 f'(x) 倍.

假设想要估算 $\text{(6.01}{)}^2$ , 设 $\text{f(x)=}{x}^2$ 且 a=6, 则 f'(x)=2x, 所以 f(6)=12. 如果想知道当 x 从 6 增加 0.01时候, f(x)的变化, 于是有

所以 $\text{(6.01}{)}^2\approx \text{36+0.12=36.12}$

13.2.4 近似中的误差(The error in our approximation)

用 L(x) 代替 f(x) 相差越小, 近似就越精确, 误差:

其中如果函数 f 的二阶导数存在, 至少在 x 和 a 之间存在, 那么对于 r(x) 就有公式:

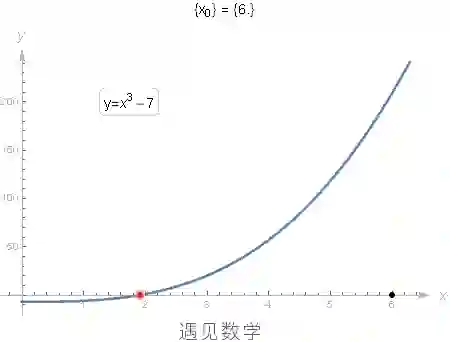
13.3 牛顿法(Newton's Method)

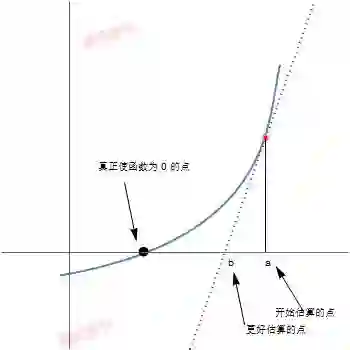
要解一个形为f(x) = 0 的方程, 但不容易直接求出, 则猜测该方程有一个解, 并把它记为 a, 然后进行迭代来改善估算的结果.

牛顿法假设a 是对方程 f(x) = 0 的解的一个近似. 如果令 $\text{b = a -}\frac{f\left(a\right)}{f^{\prime }\left(a\right)}$ . 则在很多情况下, b 是个比 a 更好的近似.

有时牛顿法也会不起作用. 下面是失效的四种不同情况(图形请查看书)(1) f'(a) 的值接近于0.(2) 如果f(x) = 0 有不止一个解, 可能得到的不是你想要的那个解.(3) 近似可能变得越来越糟.(4) 可能陷入一个循环(完)

「予人玫瑰, 手留余香」

转发既是支持帮助[遇见数学]更快发展, 非常感谢!