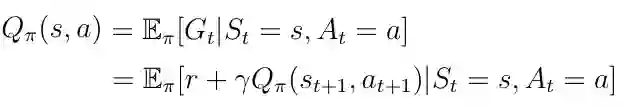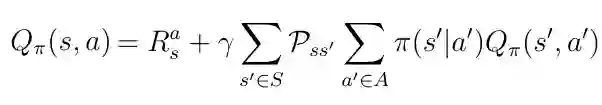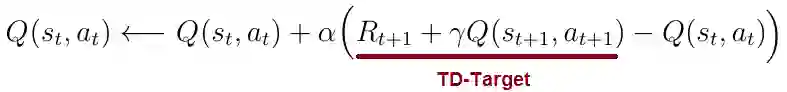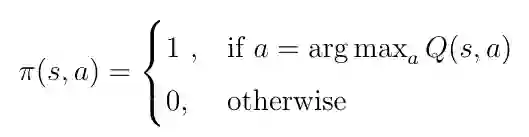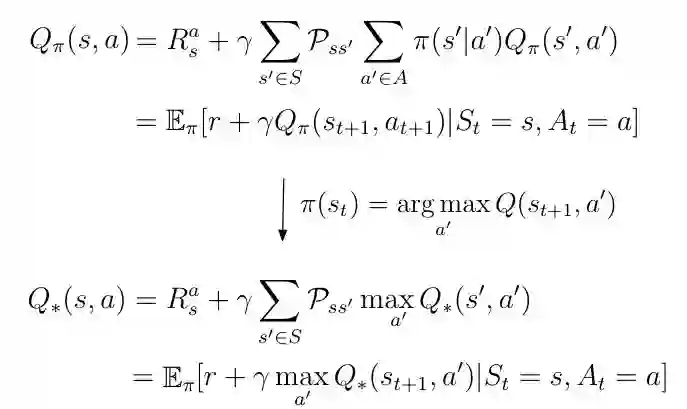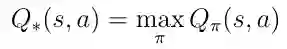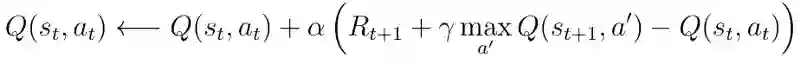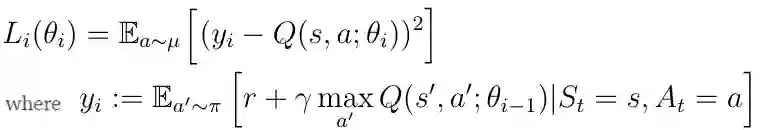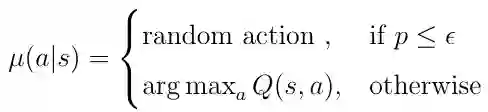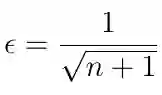自学习 AI 智能体第二部分：深度 Q 学习

本文为 AI 研习社编译的技术博客，原标题 ：

Self Learning AI-Agents Part II: Deep Q-Learning

翻译 | 老赵    校对 | 酱番梨    整理 | 菠萝妹

原文链接：

https://towardsdatascience.com/self-learning-ai-agents-part-ii-deep-q-learning-b5ac60c3f47

注：本文的相关链接请点击文末【阅读原文】进行访问

深度学习的数学指导。 在关于深度强化学习的多系列的第二部分中，我将向你介绍 AI 主体如何学习在具有离散动作空间的环境中表示的有效方法。

  自学习 AI 主体系列 - 目录

•       第一部分：马尔可夫决策过程

•       第二部分：深度Q学习（本文）

•       第三部分：深入（双重）Q-Learning

•       第四部分：继续行动空间的策略梯度

•       第五部分：决斗网络

•       第六部分：异步动作 - 批评主体

  深度 Q-Learning - 目录

       0. 简介

       1. 时间差异学习

       2. Q-Learning

              2.1 开关策略

              2.2 贪心策略

       3. 深入的Q-Learning

              3.1 目标和Q网络

              3.2 ε-贪心策略

              3.3 探索/开发困境

              3.4 体验重放

        4. 体验重放伪算法的深度Q学习

  0. 简介

在本系列的第一篇文章中，介绍了马尔可夫决策过程的概念，它是深度强化学习的基础。为了完全理解以下主题，建议回顾第一篇文章。

通过深度 Q 学习，我们编写可以在具有离散动作空间的环境中运行的 AI 主体。 离散动作空间指的是明确定义的动作，例如， 向左或向右，向上或向下移动。

图1.  Atari的突破作为离散动作空间的一个例子。

Atari的突破是具有离散动作空间的环境的典型示例。 AI 主体可以向左或向右移动。 每个方向的运动都以一定的速度发生。

如果主体可以确定速度，那么我们将拥有一个具有无限可能动作的持续动作空间（具有不同速度的运动）。 将来会考虑这个案例。

动作价值函数

在上一篇文章中，我介绍了由等式1给出的动作价值函数 Q（s，a）的概念。作为提醒，动作价值函数被定义为 AI 主体通过从状态 s 开始，采取动作 a 然后遵循策略 π 而获得的预期回报。

 注意：直观地说，策略 π 可以被描述为主体根据当前状态选择某些动作的策略。

等式1.  动作价值函数

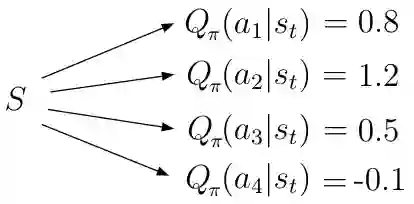
Q（s，a）告诉主体在特定状态 s 中可能的动作 a 的值（或质量）。 给定状态 s，动作价值函数计算该状态下每个可能动作 a_i 的质量/值作为标量值（图1）。 更高的质量意味着在给定目标方面采取更好的行动。

图1 给定状态 s，Q（s，a）有很多动作和适当的值

如果在等式1中执行期望运算符 E，在处理概率时我们可以获得一种新形式的动作价值函数。 Pss' 是从状态 s 到下一个状态 s' 的转换概率，由环境决定。 π（s'| a'）是策略或数学上讲给定状态s的所有动作的分布。

等式2  Q（s，a）包含概率的另一形式

  1.时间差异学习

深度 Q 学习的目标是解决动作价值函数 Q（s，a）。 我们为什么要这样？ 如果 AI 主体知道 Q（s，a），那么给定目标（比如赢得国际象棋比赛与人类玩家或玩Atari的突破）可以被视为已经解决。 其原因在于，Q（s，a）的知识将使主体能够确定在任意给定状态下任何可能动作的质量。 因此，主体可以相应地表示。

等式2给出了一个递归解决方案，可用于计算Q（s，a）。 但是，由于我们正在考虑递归并且使用该等式处理概率是不实际的。 相反，我们必须使用所谓的时间差（TD）学习算法来迭代地求解Q（s，a）。

在时间差学习中，我们将状态 s 中的每个动作 a 的 Q（s，a）更新为估计的返回 R（t + 1）+γQ（s（t + 1），a（t + 1））（等式3））。 返回估计也称为TD-目标。 对每个状态 s 和动作 a 迭代地执行此更新规则，在环境中的任何状态 - 动作对产生正确的动作价值Q（s，a）。

等式3  Q（s，a）更新规则

TD-Learning算法可以通过以下步骤进行总结：

• 计算状态s_t中动作a_t的Q（s_t，a_t）

• 转到下一个状态s_（t + 1），在那里执行动作a（t + 1）并计算值Q（s_（t + 1），a（t + 1））

• 使用Q（s_（t + 1），a（t + 1））和立即奖励R（t + 1）用于最后状态s_t中的动作a_t来计算TD目标

• 通过将Q（s_t，a_t）添加到TD目标和Q（s_t，a_t）之间的差值来更新先前的Q（s_t，a_t），α是学习速率。

1.1 时间差异

让我们更详细地讨论TD算法的概念。 在TD学习中，我们考虑Q（s，a）的“时间差异” - Q（s，a）的两个“版本”之间的差异，在我们在状态 s 中执行动作 a 之前和之后的时间之间分隔一次。

采取动作之前：

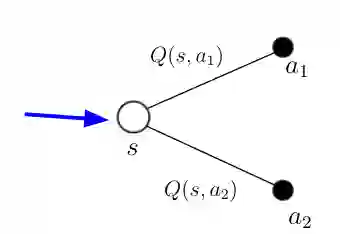
图2. 假设 AI 主体处于状态 s（蓝色箭头）。 在状态 s 中，可以采取两种不同的动作 a_1 和 a_2。 基于来自先前时间步骤的计算，主体知道在该状态下两个可能动作的动作价值Q（s，a_1）和Q（s，a_2）。

图2 状态 s 中的主体知道每个可能的Q（s，a）

采取动作之后：

根据这些知识，主体决定采取动作 a_1。 采取此行动后，主体处于下一个状态 s'。 为了采取行动 a_1，他收到了直接奖励 R。在状态 s' 中，主体可以再次采取两个可能的行动 a'_1 和 a'_2，他们从之前的一些计算中再次知道行动价值。

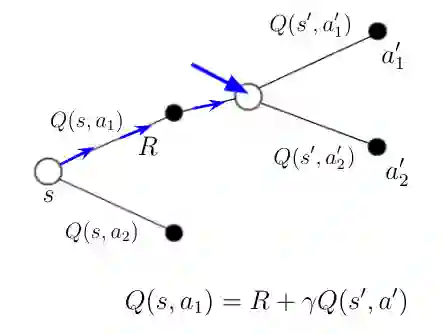
如果你看方程式1中Q（s，a）的定义。你会发现在状态 s' 我们现在有了新的信息，可以用它来计算Q（s，a_1）的新值。 该信息是针对最后状态中的最后一个动作接收的直接奖励 R 以及主体将在该新状态中采取的动作 a' 的Q（s'，a'）。 Q（s，a_1）的新值可以根据图3中的等式计算。等式的右边也是我们称之为TD目标。 TD目标与Q（s，a_1）的旧值或“时间版本”之间的差异称为时间差。

注意：在TD学习期间，我们计算任何可能的动作值Q（s，a）的时间差异，并使用它们同时更新Q（s，a），直到Q（s，a）收敛到它为真值。      

图3  主体在状态 s' 中采取动作 a_1

1.2  SARSA

应用于Q（s，a）的TD学习算法通常称为 SARSA 算法（状态-动作-奖励-状态-动作）。 SARSA是一种称为在策略的特殊学习算法的好例子。

之前介绍策略π（a | s）作为从状态s到动作a的映射。 此时你应该记住的一件事是，在策略算法使用相同的策略在TD目标t中来获取Q（s_t，a_t）的动作以及Q的动作（s（t + 1），a_（t + 1） ））。 这意味着我们正在同时遵循和改进相同的策略。

  2. Q学习

我们终于到达了文章的核心，我们将讨论 Q 学习的概念。 但在之前我们必须看一下被称为离策略的第二种特殊算法。 你可能认为Q学习已经属于这种算法，这与SARSA在策略算法有所区别。

要了解离策略算法，我们必须引入另一个策略μ（a | s）并将其称为行为策略。 行为策略确定针对所有t的Q（s_t，a_t）的动作a_t~μ（a | s）。 就SARSA而言，行为策略将是我们遵循的策略，并在同时尝试进行优化。

在离策略算法中，我们有两个不同的策略μ（a | s）和π（a | s），μ（a | s）是行为，π（a | s）是所谓的目标策略。 当行为策略用于计算Q（s_t，a_t）时，目标策略仅用于在TD目标中计算Q（s_t，a_t）（这个概念在下一节中会更全面，在那里进行实际计算）。

 注意：行为策略选择所有Q（s，a）的行动。 相反，目标策略仅确定用于计算TD目标的动作。

我们实际上称之为 Q 学习的算法是一种特殊情况，其中目标策略π（a | s）对于 Q（s，a）是贪心的，这意味着我们的策略是采取导致Q值最高的行动。这产生了以下目标策略：

等式4  对于 Q（s，a）得贪心目标策略

在这种情况下，目标策略称为贪心策略。  贪心策略意味着我们只挑选导致Q（s，a）值最高的行动。 其中我们遵循随机策略π（a | s）之前，这个贪心的目标策略可以插入到动作值Q（s，a）的等式中：

等式5 将贪心策略插入Q（s，a）

贪心策略为我们提供了最佳的动作值Q *（s，a），因为根据定义，Q *（s，a）是Q（s，a），它遵循最大化动作值的策略：

等式6  最优Q（s，a）的定义

等式5中的最后一行只不过我们在上一篇文章中得出的Bellman最优性方程。 该等式用作递归更新规则以估计最佳动作值函数Q *（s，a）。

然而，TD学习仍然是找到Q *（s，a）的最佳方式。 使用贪心目标策略，等式3中Q（s，a）的TD学习更新步骤变得更加简单，如下所示：

等式7  贪心策略的TD学习更新规则

具有贪心目标策略的Q（s，a）的TD学习算法可归纳为以下步骤：

• 计算状态 s_t 中动作 a_t 的Q（s_t，a_t）

•  转到下一个状态s_（t + 1），采取行动 a' 导致Q值最高并计算Q（s_（t + 1），a'）

• 使用Q（s_（t + 1），a'）和最后状态 s_t 中的动作 a_t 的立即奖励R来计算TD目标

• 通过将Q（s_t，a_t）添加到TD目标和Q（s_t，a_t）之间的差值来更新先前的Q（s_t，a_t），α是学习速率。

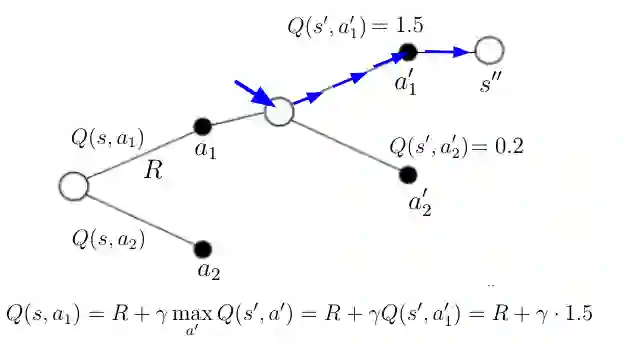
考虑前面的图（图3），其中主体在状态 s' 中并且知道该状态中可能的动作的动作值。 遵循贪心目标策略，主体将采取具有最高动作值的动作（图4中的蓝色路径）。 该策略还为Q（s，a_1）（图中的等式）提供了新值，根据定义，它是TD目标。

等式8    根据贪心策略计算Q（s，a_1）

  3. 深度Q学习

我们终于到达了这篇文章的标题 - 我们最终使用深度学习。 如果查看Q（s，a）的更新规则，你可能会发现如果TD目标和Q（s，a）具有相同的值，我们不会获得任何更新。 在这种情况下，Q（s，a）收敛到真实的行动值并实现目标。

这意味着我们的目标是最小化TD目标和Q（s，a）之间的距离，这可以用平方误差损失函数（公式10）表示。 通过通常的梯度下降算法可以实现这种损失函数的最小化。

等式10 平方误差损失函数

3.1 目标和Q网络

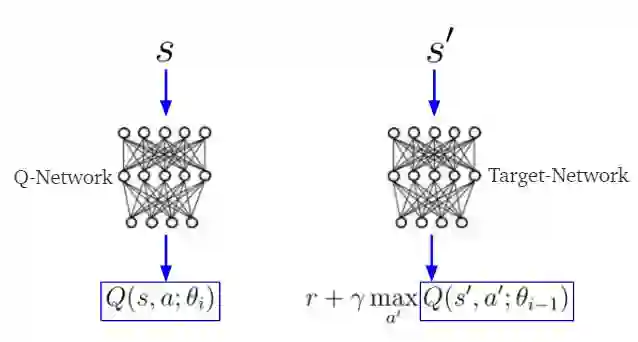
在深度Q学习TD目标中，y_i和Q（s，a）由两个不同的神经网络分别估计，这两个神经网络通常被称为目标和Q网络（图4）。 目标网络的参数θ（i-1）（权重，偏差）对应于较早时间点的Q网络的参数θ（i）。 这意味着目标网络参数会及时冻结。 它们在使用Q网络的参数进行n次迭代后得到更新。

 注意：给定当前状态s，Q网络计算动作值Q（s，a）。 同时，目标网络使用下一个状态s'来计算TD目标的Q（s'，a）。

图4目标和Q网络。 s是当前状态，s'的下一个状态。

研究表明，使用两种不同的神经网络进行TD目标t和Q（s，a）计算可以使模型具有更好的稳定性。

3.2 ε-贪心策略

当目标策略π（a | s）仍然是贪心策略时，行为策略μ（a | s）确定AI主体所采取的动作a_i，因此Q（s，a_i）（由Q网络计算）必须被插入平方误差损失函数。

行为策略通常被选为ε- 贪心策略。 利用ε-贪心策略，主体在每个时间步骤选择具有固定概率 ε 的随机动作。 如果 ε 的值高于随机生成的数字 p，0≤p≤1，则AI主体从动作空间中选择随机动作。 否则，根据倾斜的动作值Q（s，a）贪婪地选择动作：

等式11  ε-贪心策略的定义

选择ε- 贪心策略作为行为策略μ解决了探索/开发的两难选择。

3.3 探索/开发

关于采取哪些行动的决策涉及一个基本选择：

       开发：根据当前信息做出最佳决策

       探索：收集更多信息，探索可能的新途径

在利用方面，主体根据行为策略 μ 采取最佳行动。 但这可能会导致问题。 也许有时会有另一种（替代）行动可以通过状态序列在更好的路径中产生（长期），但如果我们遵循行为策略，则可能不采取这种替代行动。 在这种情况下，我们利用当前的策略，但不会探索其他替代行动。

ε-贪心策略通过允许AI主体以特定概率ε从动作空间中采取随机动作来解决该问题。 这称为探索。 通常，ε的值随着时间的推移而降低，根据等式12，这里n是迭代次数。 减少ε意味着在培训开始时我们尝试探索更多的替代路径，而最终，我们让策略决定采取哪些行动。

等式12 随着时间的推移减少ε

3.4 体验重放

在过去，可以证明，如果深度Q学习模型实现经验重放，则估计TD目标和Q（s，a）的神经网络方法变得更加稳定。 体验重放只不过是存储

      s：AI主体的状态

      a'：主体在状态内 s 采取的行动

      r：在状态 s 对应动作 a'收到的立即奖励

      s'：状态s后主体的下一个状态

在训练神经网络时，我们通常不使用最新的

3.5 体验重放伪算法的深度Q学习

以下伪算法实现了具有体验重放的深度 Q 学习。 我们之前讨论过的所有主题都以正确的顺序包含在此算法中，具体如何在代码中实现。

体验重放深度 Q 学习的伪算法

想要继续查看该篇文章相关链接和参考文献？

戳链接或点击底部【阅读原文】：

http://ai.yanxishe.com/page/TextTranslation/1180

AI研习社每日更新精彩内容，观看更多精彩内容：

使用 SKIL 和 YOLO 构建产品级目标检测系统

AI课程/书籍/视频讲座/论文精选大列表

Excel 还能这样玩？轻松搞懂一维 & 三维卷积神经网络

数据科学家应当了解的五个统计基本概念：统计特征、概率分布、降维、过采样/欠采样、贝叶斯统计

等你来译：

初学者怎样使用Keras进行迁移学习 

从语言学角度看词嵌入模型 

使用OpenCV和基于轮廓的方法实现寻线机器人 

去中心化可扩展多智能体强化学习