从源头探讨 GCN 的行文思路
加入极市专业CV交流群，与 10000+来自港科大、北大、清华、中科院、CMU、腾讯、百度 等名校名企视觉开发者互动交流！
同时提供每月大咖直播分享、真实项目需求对接、干货资讯汇总，行业技术交流。关注 极市平台 公众号 ，回复 加群，立刻申请入群~
今晚8点，极市计算机视觉开发者榜单（ECV2020）第一次线上集训来了！本次直播将为大家讲解极市训练平台使用、git和dockfile等工具使用，还有极市技术大佬线上答疑解惑。在极市平台后台回复“63”，即可获取直播链接
今年，IJCAI、CVPR、MM 上 Graph 相关的论文已经呈现井喷式的增长。相信领域内的小伙伴也都感受到了不同程度的 Peer Presure，加紧撰写或是修改论文。在相关文献中，有些文章行云流水，insight 和 GCN 的特点结合的很棒；也有些文章生硬牵强，给人一种不 make sense 的感觉。
在顺藤摸瓜梳理 GCN 的分析视角的过程中，有四个历史悠久的研究方向与 GCN 的思路异曲同工。虽然他们的光辉暂时被 GCN 掩盖，但是在优秀的 GCN 论文中，他们分析思路仍被广泛使用。
下面，我们将从简单到困难介绍这四种研究方向的基本思想、从该视角对 GCN 的理解，以及适用的领域。希望给正在写论文和找不到应用方向的小伙伴一些帮助。
PageRank —— 累计重要性
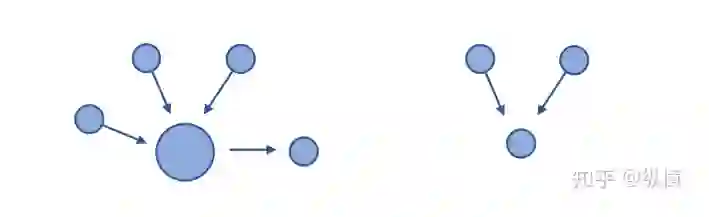
基本思想：PageRank 是一种用于量化网络中网页重要程度的算法。在 PageRank 诞生前，人们通常使用指向一个网页的网页数量来衡量该网页的重要程度（指向一个网页的网页越多，人们访问该网页的概率越大）。但是这种做法只考虑了链接（一个网页对另一个网页的指向）的数量而忽视了链接的质量，即所有链接都是同等重要的。
PageRank 解决了重要性的量化和累积问题，赋予了大流量网页更高的权重。PageRank 的做法是：
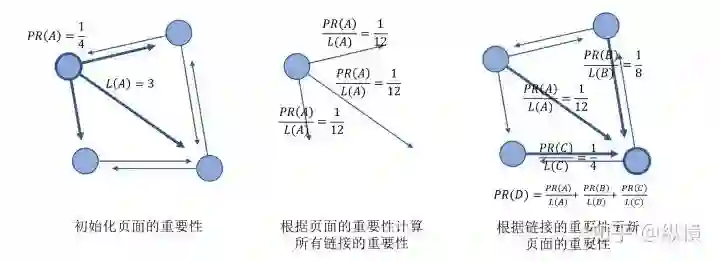
PageRank 的计算过程
1. 假设世界上总共有 4 个网页，则在不考虑链接时每个网页被访问的概率为 1/4，因此将每个网页的重要程度初始化为 1/4。将 A 网页的重要程度用 PR(A) 表示，则 PR(A)=1/4
2. 假设 A 网页共指向了 L(A) 个网页，则每个指向的重要程度（被使用的概率）为 PR(A) / L(A)
3. D 页面的重要程度可以表示为指向 D 的链接的重要程度之和，即使用下面的公式更新 D 页面的重要程度：
4. 根据所有页面新的重要程度，重复第 2、3 步，直至收敛（更新前的 PR(D) 与更新后的 PR'(D) 的差异小与某个设定的阈值）
结合GCN：考虑 GCN 中的卷积公式 ，其中 为图中每个节点的特征向量， 为图的邻接矩阵， 为度矩阵， 为训练参数（推导过程中省略）。观察 第 行的值（即图中第 个节点的特征向量是如何更新的）：
可以发现 GCN 和 PageRank 的思路大同小异，只是链接的权重 被替换为了边的权值 ，链接数量 被替换为了相邻边的权值之和 。但两者的本质都是通过边的权值计算节点的重要程度，并通过迭代（GCN 里是多层卷积）累积重要程度直至收敛。
适用方向：PageRank 方向的研究在大规模 Network 的分析和处理中积累了大量的研究经验，因此在大规模关系网络的分析和处理中，往往可以找到 PageRank 的相关分析进行解释。例如，在社交网络、推荐系统、团伙发现等任务中，往往可以强调 User 的重要性程度不同（关键用户、团伙头目等）。
Attention —— 查询重要性
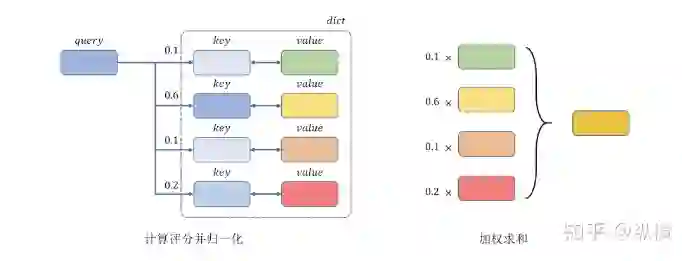
基本思想：Attention 是一种能够进行（一般用于长上下文或状态集合中）信息抽取的网络结构。Attention 的实质是使用查询条件（query）在一个包含大量键值对（key-value）的字典中，匹配符合要求的 key 并获得对应的 value 的过程。令 query 为 ，第 个 key 对应的 value 为 ，Attention 机制可以被描述为以下三部分：
-
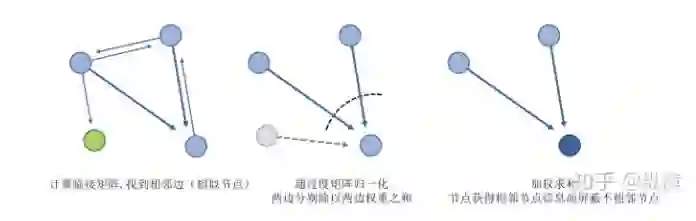
计算 query 与所有 key 的相似度，得到评分。以下四种方法都较为常见：
2. 使用 Softmax 对评分进行归一化：
3. 将归一化后的评分与 value 加权求和得到 Attention 的结果：
在自然语言处理任务中，key 和 value 通常相同，即都为输入的一系列词向量，query 为当前状态。这样，网络就可以像人类一样，忽略不想关注的部分，而从需要关注的词向量提取信息。
除了这种静态的 Attention 外，Self-Attention 和 Transformer 也被广泛使用在自然语言处理和计算机视觉任务中。在 Self-Attention 中，原始向量到 query、key、value 的映射是可以通过反向传播学习的，因此不再需要我们手动定义 query 与 key 的相似度的计算方法。
上文中的操作可以替换为：
其中， 、 和 为训练参数。
结合GCN：观察 GCN 中的卷积公式 ，其中 为图中每个节点的特征向量， 为图的邻接矩阵， 为度矩阵， 为训练参数（推导过程中省略）。其实，这个过程可以理解为，通过邻接矩阵 定义了当前节点与周围节点的相似度评分，即 。使用度矩阵（当前节点所有相邻边的权值之和）的倒数 对评分进行了归一化。最后通过乘 完成了对 value 的提取。
在此基础上，也有同学提出了 Graph Transformer 进行 Self-Attention。
1. 对于当前节点 对应的特征向量 和相邻节点 对应的特征向量 ，他们的相似度评分为：
2. 使用 Softmax 对评分进行归一化：
3. 将归一化后的评分与 value 加权求和得到 Attention 的结果：
适用方向：Attention 方向的研究在计算机视觉和自然语言处理等方向都得到了长足发展。以计算机视觉领域为例子，例如，Attention 可以分为对 channel 和对 feature map 的 attention。feature map 中包含 ROI，而 channel 可以代表颜色、深度、轮廓、时间序列等信息，这些信息都可以作为 Graph 中的 Node 进行 Attention。（图像标注、视频内容分析等）
Spectral Clustering —— 局部特征保留
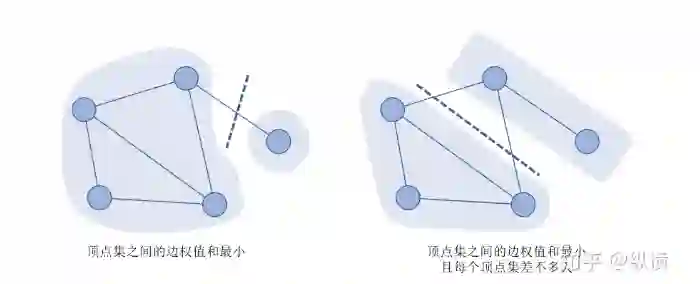
基本思想：Spectral Clustering 是一种用于图的聚类算法。图上的聚类可以理解为图的割，即将图划分为不同顶点集，使得顶点集之间的边权值和最小。但是，这样的优化目标容易导致聚类后的到的簇很不均匀（为了最小化割边的权值，算法会只割一条边）。因此，我们需要对优化目标进行归一化，即在优化聚类目标的同时，需要保证每个顶点集差不多大。
假设我们将图 划分为 个部分 ， 表示顶点集 和其他顶点集之间的边的权值和。优化目标『将图划分为不同顶点集，使得顶点集之间的边权值和最小』可以表示为：
通常，我们使用 即顶点集 中顶点的度之和度量顶点集的大小（比起顶点数量，我们更关注边的数量），来对优化目标进行归一化：
对目标函数进行化简：
令 ，
可得：
将 代入化简后的目标函数，目标函数可以化简为：
其中， 为拉普拉斯矩阵，其中 为度矩阵， 为邻接矩阵。最小化上式即最小化：
约束为 。
该式可以转化为瑞立熵公式，我们令 ，上式可以转化为：
由 Rayleigh quotient 可以知道，如果 ，那么 的最小值为 的最小特征值，该值在 为特征值对应的特征向量时取到。
也就是说，我们只需要求 的特征值并选择最小的 个特征值对应的特征向量，（往往无法直接通过维数约简获得结果，需要再对其进行一次 KMeans 聚类）就可以得到聚类的结果了。
结合GCN：Spectral Clustering 的实质是使用拉普拉斯特征映射在降维的同时保留局部特征（原本距离较近的特征点在特征映射之后距离仍然近，原本距离较远的特征点在特征映射之后仍然远），在此基础上使用聚类算法（如KMeans）对降维后的特征点进行聚类。 的特征向量具有保留局部特征的作用。因此，GCN 的卷积公式 可以近似看做通过仿射变换求特征向量的过程。
适用方向：Laplacian Eigenmaps 是流形学习的研究内容之一，因此在流行学习任务上（例如人脸识别中人脸特征随光照、方向等因素连续变化）往往可以找到 LLP、ISOMAP 的相关分析进行解释。因此，如果能够确定数据集的分布处于一个流形上，或是需要根据相似度手动构建 Graph 时，该研究方向是非常值得借鉴的，研究过程中可以使用可视化等方法佐证自己的理论（流形的可视化较为简单）。
Graph Fourier Transformation —— 频域特征变换
基本思想：与图像信号处理中的空域信号（又叫像素域，描述像素的特征，可以对像素进行叠加）和频域信号（描述空域的变化，通过傅立叶变换得到）相似，图信号处理中也有顶点域信号和频域。其中顶点域信号对应图中每个顶点的特征（例如社交网络中的年龄、爱好等），频域信号对应另一种信号分析维度（图的傅立叶变换基），描述了相邻顶点的特征差异。
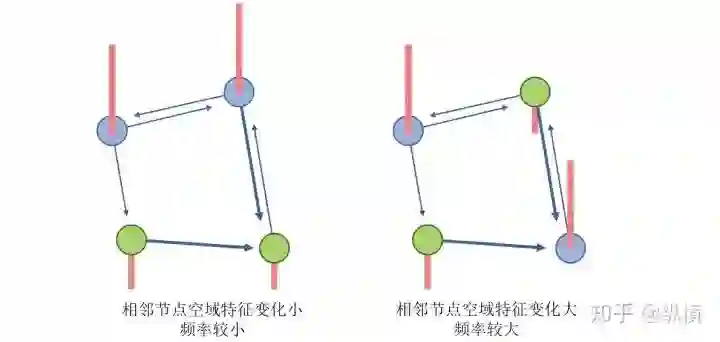
频域信号描述了相邻顶点的特征差异
令 为顶点数量， 为邻接矩阵， 为空域信号（即节点特征），相邻顶点的特征差异可以被量化为：
将 代入化简后的目标函数，目标函数可以化简为对该式进行化简：
其中， 为拉普拉斯矩阵，其中 为度矩阵， 为邻接矩阵。上式可以转化为：
令 ，由 Rayleigh quotient 可以知道，如果 ，那么 的最小值为 的最小特征值，该值在 为特征值对应的特征向量时取到；那么 的最大值为 的最大特征值，该值在 为特征值对应的特征向量时取到。
也就是说，我们只需要求 的特征值 ，较大的 对应 较大，即空域信号变化较大的高频信号；较小的 对应 较大，即空域信号变化较小的低频信号。
因而，图傅立叶变换可以定义为：
其中， 为 的第 个特征向量的第 个元素， 为其共轭。可以发现，图傅立叶变换只是将傅立叶变换中的算子 替换为了 的特征向量 。二者都包含了明显的频率信息，在低频时震荡较慢（低），高频时震荡较快（变化率高）。
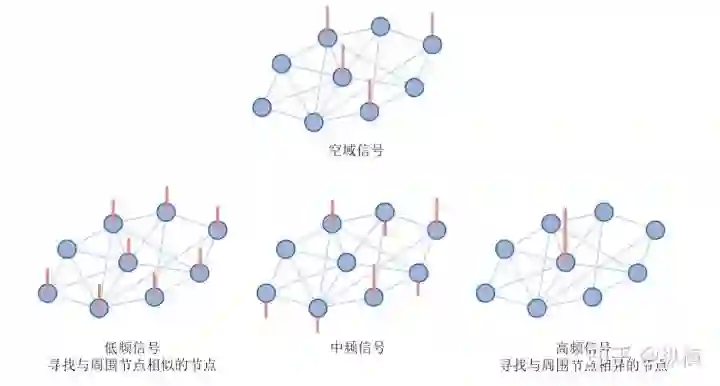
图上的频域分解
结合GCN：考虑 GCN 中的卷积公式 ，其中 为图中每个节点的特征向量， 为训练参数。**其实是将频率信息 进行了对称归一化得到 （即对称归一化的拉普拉斯矩阵），并使用训练参数对其进行了变换。**从而，GCN 具有了图上的频域叠加、平移和卷积能力。
适用方向：在四种研究方向中，频谱理论最为艰涩但是也最 make sense。约简后的频谱操作即目前适用最为广泛的 GCN，相信在未来该领域也仍是研究图卷积算子的必经之路。如果实在找不到 GCN 与当前任务的结合点，也可以直接使用该理论引出图卷积的公式（这样的顶会论文也不少）。
后记
本文只探讨了几个主要的图研究方向的视角，其实万法归一，没有提及到的很多领域也有着相似出色的工作，比如 Random Walk 等。在学习过程中希望大家能一起举一反三啦～
另外，近期准备着写一些 Vanilla PyTorch 实现图卷积的最佳实践教程，就不怎么玩知乎啦～感兴趣的同学可以关注我的 Github: tczhangzhi。此举并不是妄想重新造像 PyG 或者 DGL 一样的轮子，而是在参考了各位同学和开源库的实现后发现，Vanilla PyTorch 实现 GCN 可以让我们的代码更为简洁和灵活。因此希望总结一些最佳实践，一方面向大佬致敬，另一方面也为同学们的研究提供方便。
相关内容
微信扫码咨询专知VIP会员