换个角度看GAN：另一种损失函数

会员服务 ·

换个角度看GAN：另一种损失函数

2019 年 1 月 1 日 机器之心

选自Medium

作者：Phúc Lê

机器之心编译

参与：张玺

「本质上，GAN 就是另一种损失函数。」

Jeremy Howardf 老师曾在生成对抗网络（GAN）课程中说过：「……本质上，GAN 就是另一种损失函数。」

本文将在适合的相关背景下讨论上面的观点，并向大家阐述 GAN 这种「学得」（learned）损失函数的简洁优美之处。

首先，我们先介绍相关背景知识：

从函数逼近的角度看神经网络

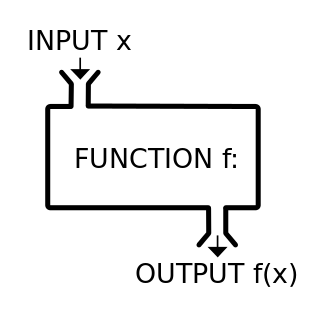
在数学中，我们可以把函数当做机器，往机器中输入一或多个数字，它会相应地生成一或多个数字。

将函数比作「机器」或「黑箱」。（图源：https://www.wikiwand.com/en/Function_%28mathematics%29）

如果我们能够用数学公式表示函数，这很好。可如果大家不能或尚未想明白如何将想要的函数写成一系列加减乘除（譬如分辨输入是猫图像还是狗图像的函数）又该如何呢？

如果无法用公式表达，那我们能否至少逼近函数呢？

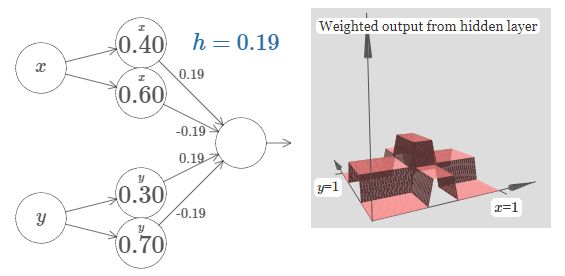
神经网络来拯救我们了。万能逼近定理表明，一个具有充足隐藏单元且足够大的神经网络可以计算「任何函数」。

具备 4 个隐藏单元的简单神经网络逼近塔型函数。（图源：http://neuralnetworksanddeeplearning.com/chap4.html）

神经网络的显式损失函数

掌握神经网络后，我们就可以构建一个神经网络以逐步逼近上文所述的猫狗分类函数，而无需显式地表达该分类函数。

为了获得更好的函数逼近能力，神经网络首先需要知道其当前性能有多差。计算神经网络误差的方式被称为损失函数。

目前已经有很多损失函数，对于损失函数的选择依赖于具体任务。然而，所有损失函数具有一个共同特性──它必须能以精确的数学表达式表示损失函数。

L1 损失（绝对误差）：用于回归任务
L2 损失（平方误差）：与 L1 类似，但对于异常值更加敏感
交叉熵误差：通常用于分类任务
Dice 损失 (IoU) ：用于分割任务
KL 散度：用于衡量两种分布之间的差异
……

关于神经网络逼近特性的好坏，损失函数承担着十分重要的作用。对于神经网络构建人员来说，针对具体任务去理解和选择恰当的损失函数是最重要的技能。

目前，设计更好的损失函数也是活跃度极高的研究领域。譬如，论文《Focal Loss for Dense Object Detection》介绍了一种名为「Focal loss」的新型损失函数，用于解决单阶段目标检测模型的不平衡性。

显式损失函数的局限

前文所述的损失函数在分类、回归及图像分割等任务中的表现相当不错，而针对输出具有多模态分布的情况，则效果堪忧。

以黑白图片着色任务为例。

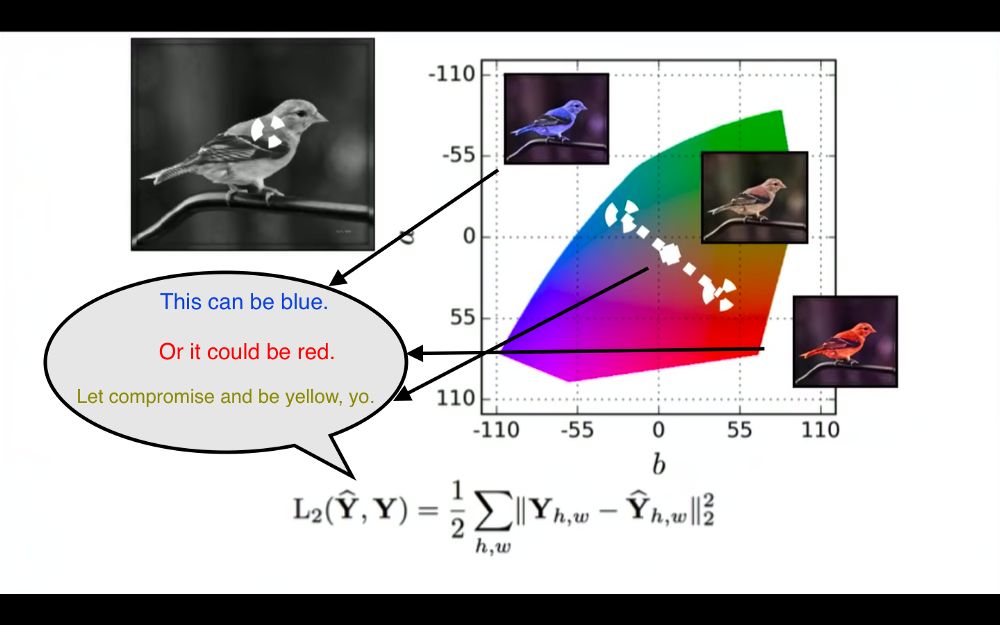
L2 损失函数的思考过程。（图源：https://youtu.be/8881p8p3Guk?t=2971）

输入是黑白色的鸟，真实图像是相同的蓝色的鸟。
采用 L2 损失函数计算模型的输出颜色与真实图像的像素级差异。
接下来，输入是与刚才实验相似的一只黑白色的鸟；真实图像是一只相同的红色的鸟。
L2 损失函数试图最小化模型的输出颜色与红色的差异。
基于 L2 损失函数的反馈，模型已学习出一只相似的鸟，但模型应该输出一种与红色及蓝色都接近的颜色。模型会怎么做？
模型会输出一种黄色的鸟，这是最小化红色与蓝色距离的最安全选择，即便模型在训练过程中从未观察到一只黄色的鸟。
由于实际上没有黄色鸟，所以你知道模型不够逼真。

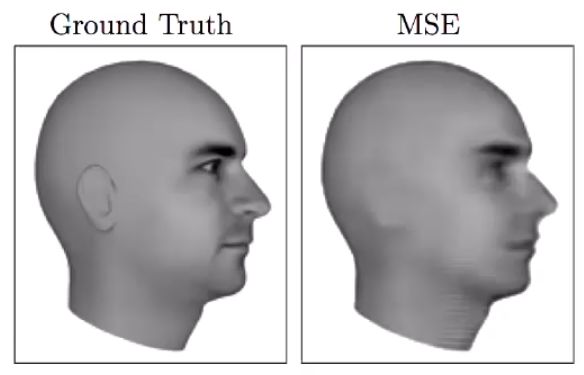
基于均方差预测的下一帧图像非常模糊。（图源：https://arxiv.org/pdf/1605.08104.pdf）

这种均化效应在许多实例中会导致非常糟糕的结果。以预测视频下一帧任务为例，下一帧的可能性非常多，你想要的是能输出「其中某一帧」的模型。但是，如果采用 L2 或 L1 训练模型，模型将平均所有可能结果，生成一张十分模糊的均化图像。

GAN 作为新的损失函数

首先，你并不知道复杂函数的精确数学表达式（比如函数的输入是一组数字，输出是一张狗狗的逼真图像），所以你使用神经网络逼近此函数。

神经网络需要损失函数告知它目前性能的好坏，但没有任何显式损失函数能够很好的完成此项工作。

嗯，要是有一种既无需显式数学表达式，又能够直接逼近神经网络损失函数的方法，该多好。譬如神经网络？

所以，如果我们用神经网络模型替代显式损失函数，将会怎样？恭喜，你发现了 GAN。

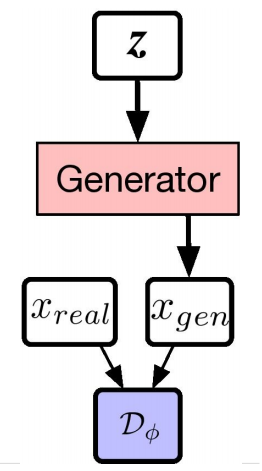
通过下面的 GAN 架构和 Alpha-GAN 架构，你能观察地更清晰。如图，白色框代表输入，粉色框和绿色框代表你想构建的网络，蓝色框代表损失函数。

GAN 架构。（图源：http://efrosgans.eecs.berkeley.edu/CVPR18_slides/VAE_GANS_by_Rosca.pdf）

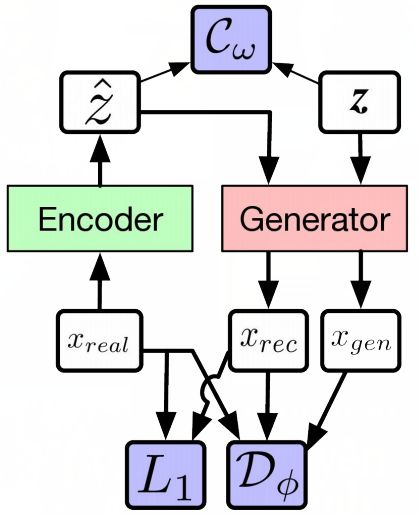
Alpha-GAN 架构。（图源：http://efrosgans.eecs.berkeley.edu/CVPR18_slides/VAE_GANS_by_Rosca.pdf）

在原版 GAN 中仅有一种损失函数——判别器网络 D，其自身就是另一种神经网络。

而在 Alpha-GAN 中，模型有 3 种损失函数：输入数据的判别器 D、用于已编码潜变量的潜码判别器 C，以及传统像素级 L1 损失函数。其中，D 和 C 并不是显式损失函数，而只是其近似──神经网络。

梯度

如果将判别器（同样也是神经网络）作为损失函数来训练生成器网络（与 Alpha-GAN 的编码器），那么用什么损失函数来训练判别器呢？

判别器的任务是区分真实数据分布与生成数据分布。用监督方式训练判别器时，标签可随意使用，所以采用二元交叉熵等显式损失函数训练判别器就很简单。

但由于判别器是生成器的损失函数，这代表判别器的二元交叉熵损失函数的累积梯度同样会被用于更新生成器网络。

观察 GAN 中的梯度变化，就非常容易发现改变其轨迹的新思路。如果显式损失函数的梯度无法在两个神经网络间（判别器和生成器）回流，却可以在三个神经网络间回流，那么它能被应用在何处？如果梯度无法通过传统损失函数回流，却可在这些神经网络之间直接来回呢？从基本原理出发，我们很容易发现未被探索的路径以及未被解答的问题。

结论

通过传统损失函数与神经网络的集成，GAN 使将神经网络作为损失函数来训练另一神经网络成为可能。两个神经网络间的巧妙交互使得深度神经网络能够解决一些先前无法完成的任务（如生成逼真图像）。

将 GAN 本质上视为一种学得的损失函数，我希望这篇文章能够帮助大家理解 GAN 的简洁和力量。