【经典重读】统计学习那些事

2017 年 11 月 5 日 专知杨灿

点击上方“专知”关注获取更多AI知识!

【导读】这是杨灿博士在早年写的关于统计学习的一些见解，尤其关于Lasso与Boosting。当年我读博2011年时期间看到这篇文章，也是受益良多。作者文采很棒，《悟空传》“你不觉得天边的晚霞很美吗？只有看着她，我才能坚持向西走。” 推荐给大家！

作者简介：杨灿，香港科技大学电子与计算机工程系。

主页：http://ihome.ust.hk/~eeyang/index.html

在港科大拿到 PhD，做的是 Bioinformatics 方面的东西。Bioinformatics 这个领域很乱，从业者水平参差不齐，但随着相关技术（比如 Microarray, Genotyping）的进步，这个领域一直风风光光。因为我本科是学计算机电子技术方面的，对这些技术本身并没有多大的兴趣，支持我一路走过来的一个重要原因是我感受到统计学习 (Statistical learning) 的魅力。正如本科时代看过的一本网络小说《悟空传》所写的：“你不觉得天边的晚霞很美吗？只有看着她，我才能坚持向西走。”

离校前闲来无事，觉得应该把自己的一些感受写下来，和更多的爱好者分享。

1. 学习经历

先介绍一下我是如何发现这个领域的。我本科学自动化，大四时接触到一点智能控制的东西，比如模糊系统，神经网络。研究生阶段除了做点小硬件和小软件，主要的时间花在研究模糊系统上。一个偶然的机会，发现了王立新老师的《模糊系统与模糊控制教材》。我至今依然认为这是有关模糊系统的最好的书，逻辑性非常强。它解答了我当年的很多困惑，然而真正令我心潮澎湃的是这本书的序言，读起来有一种 “飞” 的感觉。后来我终于有机会来到港科大，成为立新老师的 PhD 学生，时长一年半（因为立新老师离开港科大投身产业界了）。立新老师对我的指导很少，总结起来可能就一句话：“你应该去看一下 Breiman 和 Friedman 的文章。”立新老师在我心目中的位置是高高在上的，于是我就忠实地执行了他的话。那一年半的时间里，我几乎把他们的文章看了好几遍。开始不怎么懂，后来才慢慢懂了，甚至有些痴迷。于是，我把与他们经常合作的一些学者的大部分文章也拿来看了，当时很傻很天真，就是瞎看，后来才知道他们的鼎鼎大名，Hastie, Tibshirani, Efron 等。文章看得差不多了，就反复看他们的那本书“The Elements of Statistical learning”（以下简称 ESL）。说实话，不容易看明白，也没有人指导，我只好把文章和书一起反复看，就这样来来回回折腾。比如为看懂 Efron 的“Least angle regression”，我一个人前前后后折腾了一年时间（个人资质太差）。当时国内还有人翻译了这本书（2006 年），把名字翻译为“统计学习基础”。我的神啦，这也叫“基础”！还要不要人学啊！难道绝世武功真的要练三五十年？其实正确的翻译应该叫“精要”。在我看来，这本书所记载的是绝世武功的要义，强调的是整体的理解，联系和把握，绝世武功的细节在他们的文章里。

2. 关于 Lasso 与 Boosting

由于篇幅有限，我就以 Lasso 和 Boosting 为主线讲讲自己的体会。故事还得从 90 年代说起。我觉得 90 年代是这个领域发展的一个黄金年代，因为两种绝世武功都在这个时候横空出世，他们是 SVM 和 Boosted Trees。

先说 SVM。大家对 SVM 的基本原理普遍表述为，SVM 通过非线性变换把原空间映射到高维空间，然后在这个高维空间构造线性分类器，因为在高维空间数据点更容易分开。甚至有部分学者认为 SVM 可以克服维数灾难 (curse of dimensionality)。如果这样理解 SVM 的基本原理，我觉得还没有看到问题的本质。因为这个看法不能解释下面的事实：SVM 在高维空间里构建分类器后，为什么这个分类器不会对原空间的数据集 Overfitting 呢？要理解 SVM 的成功，我觉得可以考虑以下几个方面：第一，SVM 求解最优分类器的时候，使用了 L2-norm regularization，这个是控制 Overfitting 的关键。第二，SVM 不需要显式地构建非线性映射，而是通过 Kernel trick 完成，这样大大提高运算效率。第三，SVM 的优化问题属于一个二次规划（Quadratic programming），优化专家们为 SVM 这个特殊的优化问题设计了很多巧妙的解法，比如 SMO（Sequential minimal optimization）解法。第四，Vapnika 的统计学习理论为 SVM 提供了很好的理论背景（这点不能用来解释为什么 SVM 这么 popular，因为由理论导出的 bound 太 loose）。于是 SVM 成功了，火得一塌糊涂！

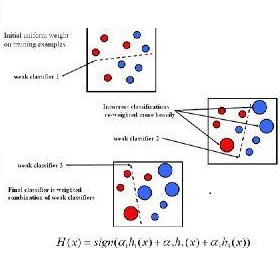
再说 Boosted Trees。它基本的想法是通过对弱分类器的组合来构造一个强分类器。所谓 “弱” 就是比随机猜要好一点点；“强”就是强啦。这个想法可以追溯到由 Leslie Valiant 教授（2010 年图灵奖得主）在 80 年代提出的 probably approximately correct learning (PAC learning) 理论。不过很长一段时间都没有一个切实可行的办法来实现这个理想。细节决定成败，再好的理论也需要有效的算法来执行。终于功夫不负有心人， Schapire 在 1996 年提出一个有效的算法真正实现了这个夙愿，它的名字叫 AdaBoost。AdaBoost 把多个不同的决策树用一种非随机的方式组合起来，表现出惊人的性能！第一，把决策树的准确率大大提高，可以与 SVM 媲美。第二，速度快，且基本不用调参数。第三，几乎不 Overfitting。我估计当时 Breiman 和 Friedman 肯定高兴坏了，因为眼看着他们提出的 CART 正在被 SVM 比下去的时候，AdaBoost 让决策树起死回生！Breiman 情不自禁地在他的论文里赞扬 AdaBoost 是最好的现货方法（off-the-shelf，即 “拿下了就可以用” 的意思）。其实在 90 年代末的时候，大家对 AdaBoost 为什么有如此神奇的性能迷惑不解。1999 年，Friedman 的一篇技术报告 “Additive logistic regression: a statistical view of boosting” 解释了大部分的疑惑（没有解释 AdaBoost 为什么不容易 Overfitting，这个问题好像至今还没有定论），即搞清楚了 AdaBoost 在优化什么指标以及如何优化的。基于此，Friedman 提出了他的 GBM（Gradient Boosting Machine，也叫 MART 或者 TreeNet）。几乎在同时，Breiman 另辟蹊径，结合他的 Bagging (Bootstrap aggregating) 提出了 Random Forest （今天微软的 Kinect 里面就采用了 Random Forest，相关论文 Real-time Human Pose Recognition in Parts from Single Depth Images 是 CVPR2011 的 best paper）。

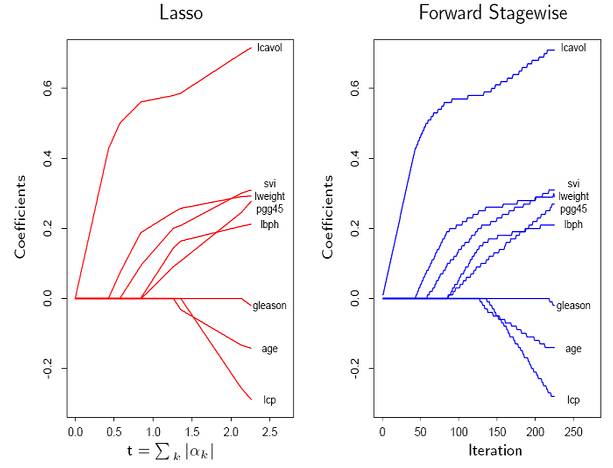
有一个关于 Gradient Boosting 细节不得不提。Friedman 在做实验的时候发现，把一棵新生成的决策树，记为 f_m，加到当前模型之前，在这棵决策树前乘以一个小的数，即 v×f_m（比如 v=0.01），再加入到当前模型中，往往大大提高模型的准确度。他把这个叫做 “Shrinkage”。接下来，Hastie，Tibshirani 和 Friedman 进一步发现（我发现大师们都是亲自动手写程序做实验的），如果把具有 Shrinkage 的 Gradient Boosting 应用到线性回归中时，得到的 Solution Path 与 Lasso 的 Solution Path 惊人地相似 (如图所示)！他们把这一结果写在了 ESL 的第一版里，并推测这二者存在着某种紧密的联系，但精确的数学关系他们当时也不清楚。Tibshirani 说他们还请教了斯坦福的优化大师（我估计是 Stephen Boyd），但还是没有找到答案。

后来 Tibshirani 找到自己的恩师 Efron。Tibshirani 在 “The Science of Bradley Efron” 这本书的序言里写道，“He sat down and pretty much single-handedly solved the problem. Along the way, he developed a new algorithm, ‘least angle regression,’ which is interesting in its own right, and sheds great statistical insight on the Lasso.” 我就不逐字逐句翻译了，大意是：Efron 独自摆平了这个问题，与此同时发明了 “Least angle regression (LAR)”。Efron 结论是 Lasso 和 Boosting 的确有很紧密的数学联系，它们都可以通过修改 LAR 得到。更令人惊叹的是 LAR 具有非常明确的几何意义。于是，Tibshirani 在序言中还有一句，“In this work, Brad shows his great mathematical power–not the twentieth century, abstract kind of math, but the old-fashioned kind: geometric insight and analysis.” 读 Prof Efron 的文章，可以感受到古典几何学与现代统计学的结合之美（推荐大家读读 Efron 教授 2010 年的一本新书 Large-Scale Inference，希望以后有机会再写写这方面的体会）！总之，Efron 的这篇文章是现代统计学的里程碑，它结束了一个时代，开启了另一个时代。

这里，想补充说明一下 Lasso 的身世，它的全称是 The Least Absolute Shrinkage and Selection Operator，读音不是 [‘læso] 而是[læ’su:]，有中文翻译为“套索”，个人觉得这个翻译不好，太远离它本来的含义，不如就用 Lasso。Tibshrani 自己说他的 Lasso 是受到 Breiman 的 Non-Negative Garrote（NNG）的启发。 Lasso 把 NNG 的两步合并为一步，即 L1-norm regularization。Lasso 的巨大优势在于它所构造的模型是 Sparse 的，因为它会自动地选择很少一部分变量构造模型。现在，Lasso 已经家喻户晓了，但是 Lasso 出生后的头两年却很少有人问津。后来 Tibshirani 自己回忆时说，可能是由下面几个原因造成的：1. 速度问题：当时计算机求解 Lasso 的速度太慢；2. 理解问题：大家对 Lasso 模型的性质理解不够（直到 Efron 的 LAR 出来后大家才搞明白）；3. 需求问题：当时还没有遇到太多高维数据分析的问题，对 Sparsity 的需求似乎不足。Lasso 的遭遇似乎在阐释我们已经熟知的一些道理： 1. 千里马常有，而伯乐不常有（没有 Efron 的 LAR，Lasso 可能很难有这么大的影响力）。2. 时势造英雄（高维数据分析的问题越来越多，比如 Bioinformatics 领域）。3. 金子总是会闪光的。

LAR 把 Lasso （L1-norm regularization）和 Boosting 真正的联系起来，如同打通了任督二脉（数学细节可以参考本人的一个小结，当然最好还是亲自拜读 Efron 的原著）。LAR 结束了一个晦涩的时代：在 LAR 之前，有关 Sparsity 的模型几乎都是一个黑箱，它们的数学性质（更不要谈古典的几何性质了）几乎都是缺失。LAR 开启了一个光明的时代：有关 Sparsity 的好文章如雨后春笋般地涌现，比如 Candes 和 Tao 的 Dantzig Selector。伯克利大学的 Bin Yu 教授称 “Lasso, Boosting and Dantzig are three cousins”。近年来兴起的 Compressed sensing（Candes & Tao, Donoho）也与 LAR 一脉相承，只是更加强调 L1-norm regularization 其他方面的数学性质，比如 Exact Recovery。我觉得这是一个问题的多个方面，Lasso 关注的是构建模型的准确性，Compressed sensing 关注的是变量选择的准确性。由此引起的关于 Sparsity 的研究，犹如黄河泛滥，一发不可收拾。比如 Low-rank 逼近是把 L1-norm 从向量到矩阵的自然推广（现在流行的 “用户推荐系统” 用到的 Collaborative filtering 的数学原理源于此）。有兴趣的童鞋可以参考我个人的小结。

还必须提到的是算法问题。我个人觉得，一个好的模型，如果没有一个快速准确的算法作为支撑的话，它最后可能什么也不是。看看 Lasso 头几年的冷遇就知道了。LAR 的成功除了它漂亮的几何性质之外，还有它的快速算法。LAR 的算法复杂度相当于最小二乘法的复杂度，这几乎已经把 Lasso 问题的求解推向极致。这一记录在 2007 年被 Friedman 的 Coordinate Descent（CD）刷新，至今没人打破。Hastie 教授趣称这个为 “FFT（Friedman + Fortran + Tricks）”。因为 CD 对 Generalized Lasso 问题并不能一网打尽，许多凸优化解法应运而生，如 Gradient Projection， Proximal methods，ADMM (Alternating Direction Method of Multipliers)， (Split) Bregman methods，Nesterov’s method (一阶梯度法中最优的收敛速度，Candes 的很多软件包都根据这个方法设计) 等等。哪个方法更好呢？这个就像问“谁的武功天下第一” 一样。我只能回答“王重阳以后再也没有天下第一了，东邪西毒南帝北丐，他们各有各的所长，有的功夫是这个人擅长一些，而另外几门功夫又是另一个人更擅长一些”。有关 L1 的算法可能还会大量涌现，正如优化大师 Stephen Boyd 所说（2010 年 9 月 28 日）：“God knows the last thing we need is another algorithm for the Lasso.”