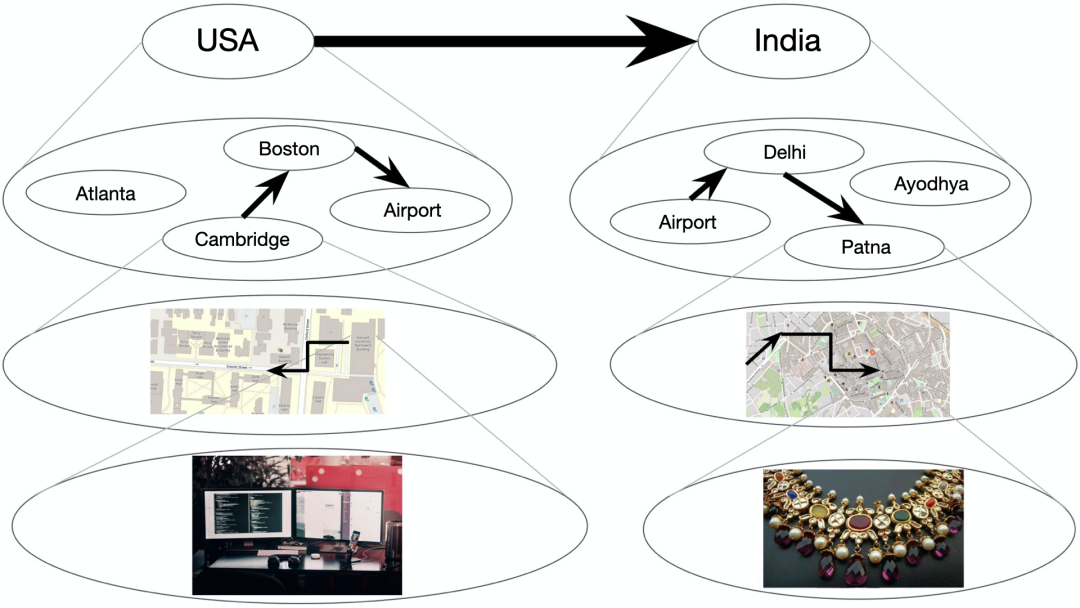
我们往往是根据事件的内容进行分层规划。无论是规划简单的事情(比如做晚餐)或复杂的事情(比如出国旅行),我们通常会率先在脑海中粗略地勾勒出想要实现的目标(比如去印度旅行完就回家,此处的目标为“旅行”与“回家”)。然后,我们会将初步想法逐步细化为一系列子目标(比如预订机票和打包行李)、子目标又再细化成更小的目标等等,直至落实到一连串的实际行动上,这比初步计划要复杂得多。
高效的规划需要具备一些抽象的高级别概念,这些概念被认为是分层规划(hierarchical plan)的精华。但是,人类是如何学习这些抽象概念的呢?这仍是未解之谜。
在本
文中,我们揭示了人类自然地形成高级概念的过程,
他们能够根据所处环境的任务、回报和系统安排进行高效地规划。
我们的研究表明,这种行为与底层计算的形式化模型是一致的,从而将这些发现建立在既定的计算原则之上,并将其与先前的分层规划研究联系起来。
上图是一个层次规划的示例,即某人如何计划从剑桥的办公室出发去购买一件在印度巴特纳的梦幻婚纱。椭圆表示状态,箭头表示在状态之间转换的操作。下方的每个椭圆代表一组较低级别的状态。较粗的箭头表示高级状态之间的转换,人类往往先想到这些概念。
从贝叶斯的角度看
当分层规划应用于计算机智能体时,它可以使模型具有高级规划能力。
从贝叶斯观点出发,分层表示可以通过假设某个特定环境的结构生成过程进行建模。
目前关于这一问题的研究工作涉及到计算框架开发,用于在一系列关于层次结构的简化假设下获取层次表示,比如对人们为了提高规划效率、如何在头脑中创建无奖励环境的状态进行建模。
在这项工作中,我们提出了分层发现的贝叶斯认知模型。
该模型结合了聚类知识和预测状态簇(cluster of states)形成的奖励。
此外,我们将该模型与从人类规划中获取的相关数据进行了比较。
我们分析了静态奖励机制和动态奖励机制这两种情形,发现人类将奖励信息泛化到高级状态簇,并利用奖励信息创建状态簇。我们提出的模型可以预测奖励泛化和基于奖励的状态簇形成。
理论背景
心理学和神经科学相结合的一个重要体现是规范理解与指定动作相关的人类行为。我们经常会疑惑:人类采用了什么样的规划和方法论来完成某项任务?人类如何发现有用的抽象概念?
鉴于人类和动物适应新环境的独特能力,上述问题非常有趣。先前关于动物学习的文献表明,这种灵活性源于目标的层次化表示,可以将复杂的任务分解成在各种环境中扩展的低级子例程(low-level subroutines)。
分块过程指的是由一个个动作编织成时间拓展的动作序列以实现未来目标。分块法(chunking)通常是学习从目标导向系统(goal-directed system)转移到惯性系统(habitual system)的结果,用刻板方式执行智能体。
从计算的角度看,这种分层表示能使智能体在开环中快速执行动作,在遇到已知问题时重复执行熟悉的动作序列,通过调整既定的动作序列解决之前遇到的类似问题、从而更快地学习,并在延长的时间范围内进行规划。
智能体不需要关心与目标达成相关的小型任务,例如去商店这个目标被分解为离开房间、步行和进入商店,而不是起床、左脚向前移动,然后右脚移动等等。
智能体如何做出能获得奖励的决定是强化学习的主题。分层强化学习(HRL)已成为表示分层学习和规划的主流框架。在HRL建模的研究中,已有几项可能的模型构建方法提出。
我们关注的是人们自发地将环境变成约束规划行为的状态簇。
这种分层规划包含了一个个低级别行动,迎合了人们有限的工作记忆能力,在时间和记忆上比简单的规划更为有效。
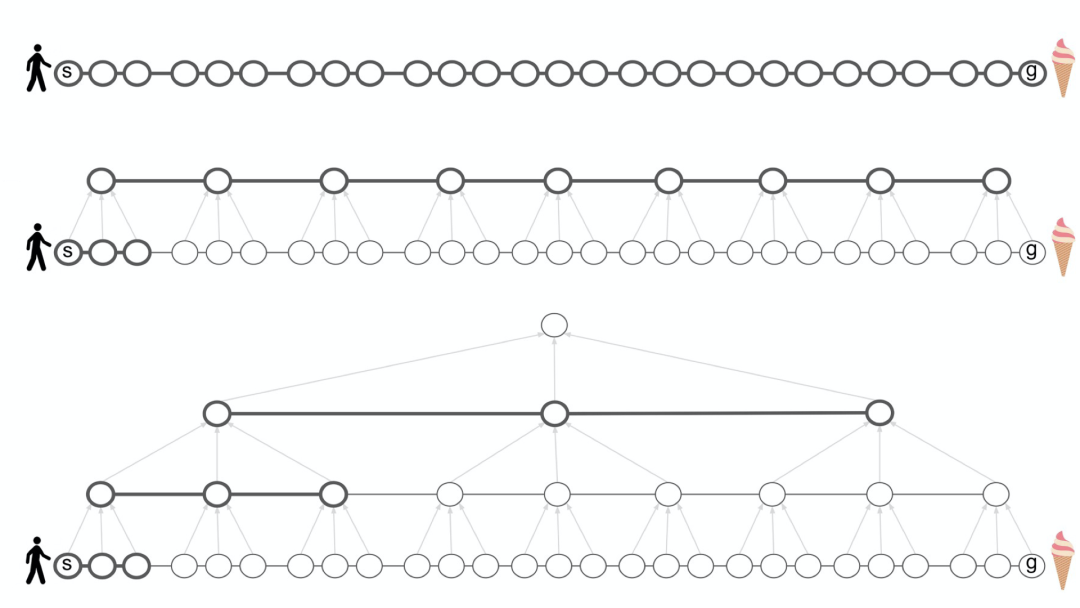
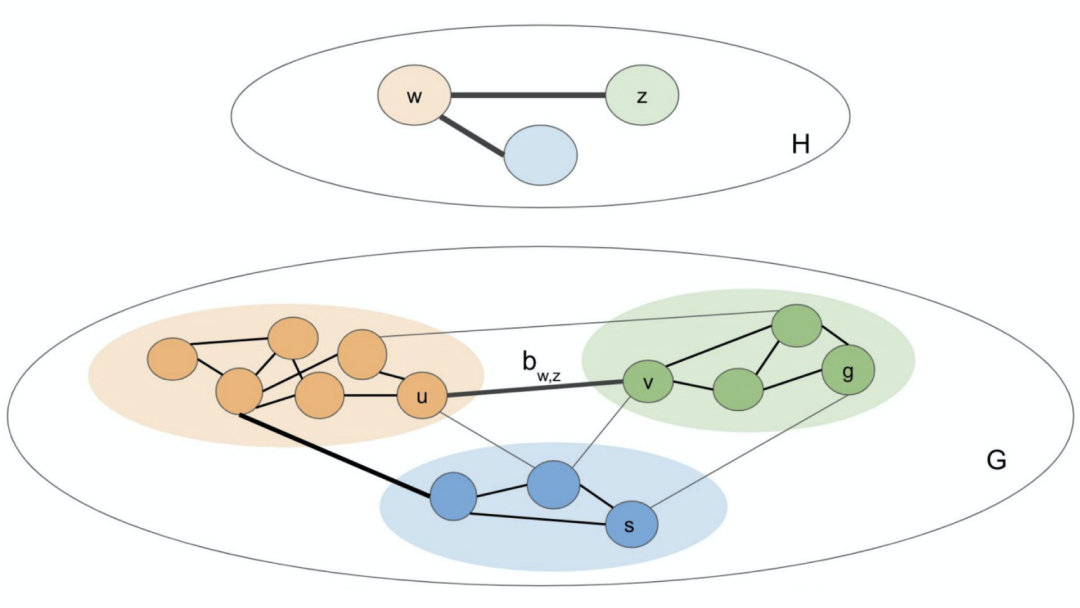
如下图所示,线条较粗的节点和边表示做规划必须考虑的、停留在短期记忆内的内容,用于对规划进行计算,而灰色箭头则表示簇的成员。我们观察到,在低级别图 G 中规划如何从状态 s 到状态 g 至少要花费与实际执行计划(下图上方)一样多的步骤,引入高级图 H 可以缓解此问题,从而降低计算成本(下图中间) ,同时扩展层次结构递归(hierarchy recursive),进一步减少规划所需的时间和记忆量(下图底部)。
![]() 分层表示降低了规划的计算成本
分层表示降低了规划的计算成本
Solway等人对最佳分层结构(optimal hierarchy)做出了一个正式的定义,但没有具体说明大脑是如何认识到最佳分层结构的[2]。我们假设最佳分层结构由环境构造决定,包括图结构与环境的可观察特征的分布(特别是奖励)。
我们假设智能体将环境表示为一张图,其中节点表示环境中的状态,边表示状态之间的转换。这些状态和转换可以是抽象的,也可以像地铁站及站与站之间的列车线一样具体。
我们将可观察的环境表示为图 G =(V,E),潜在分层表示为图H。G和H均为未加权的无向图。图H包含了状态簇(图G中的每个低级节点都恰好属于图H中的一个簇)以及连接这些簇的桥(bridge)或高级边。只有当某些 v,v'∈V 之间存在边,形成v∈k 和 v'∈k' 时,簇 k 和 k' 之间才能存在桥,比如图H中的每一条高级边在图G中都有一条相对应的低级边。
下图中,颜色表示簇分配。规划机器在做规划时主要考虑黑色边,忽略掉灰色边。粗边对应的是状态簇之间的转换,簇 w 和 z 之间的转换通过桥来实现。
在添加奖励之前,学习算法会在给出下列约束条件后找到最佳分层结构:
然而,我们不希望状态簇太小——在极
端情况下,每个节点就是它自己的状态簇,这使得分层结构没有任何用处。
此外,虽然我们希望在状态簇之间建立稀疏连接,但为了保持底层图的特性,
我们希望保留状态簇之间的桥
。
我们将离散时间随机的中餐馆过程算法(discrete-time stochastic Chinese Restaurant Process)作为状态簇的先验。分层结构的发现可以通过倒置生成模型来获得分层 H 的后验概率实现。文献[6]中提出的生成模型可生成上述的分层结构。
在图G的背景下,奖励可以解释为顶点(vertices)的可观察特征。由于人们经常基于可观察的特征进行聚类分析,因此对由奖励催生的状态簇建模是合理的[5]。此外,我们假设每个状态交付一个随机确定的奖励,而智能体的目标是将总奖励最大化[8]。
由于我们假设状态簇产生奖励,因此我们将每个状态簇建模为具有平均奖励。状态簇中的每个节点都有从以平均状态簇奖励为中心的分布中提取的平均奖励。最后,每个观察到的奖励都是从以该节点的平均奖励为中心的分布中获得。文献[1]对这一假设进行了正式讨论。
为了简化推论,我们首先假设奖励是恒定的、静止的,又将用某个固定概率在观测值之间变化的奖励标记为动态的奖励。
我们进行了两个实验来检验关于人类行为的假设和研究我们的模型对人类行为的预测能力。更重要的是,我们研究了状态簇在多大程度上推动了对奖励的推断,以及奖励在多大程度上驱动了状态簇的形成。在每个实验中,我们都收集人类数据,并将其与模型的预测结果进行比较。
状态簇催生奖励
第一个实验的目标是了解奖励如何在状态簇中泛化。我们进行了一系列测试,希望知道图结构是否驱动了状态簇的形成,以及人们是否将在一个节点上观察到的奖励泛化到了该节点所属的状态簇。
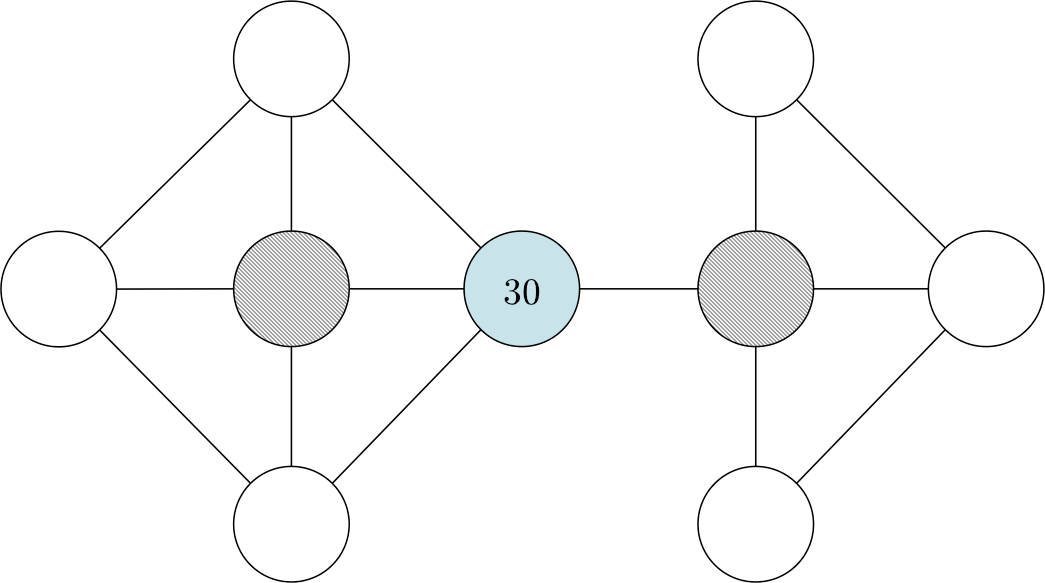
该实验让32名实验参与者按照接下来所设的场景选择下一个要访问的节点。我们向参与者随机展示下图或下图的简易版,以避免偏手性(handedness)或图结构的偏见。我们预测参与者会选择与位于较大状态簇中的标记节点相邻的节点,比如在第一种情况下,参与者会选择蓝色节点左侧的灰色节点,在第二种情况下会选择蓝色节点右侧的灰色节点。
假设你在一个巨大的金矿里工作。金矿由多个独立矿山和隧道组成。金矿的布局如下图所示(每个圆圈代表一个矿井,每条线代表一条隧道)。你的薪酬按日结算,而且当天每发现1克黄金就会获得10美元的报酬。你每天只挖一个矿,并记录下当天的黄金产量(以克为单位)。在过去的几个月里,你发现平均每个矿每天产出约15克黄金。昨天你挖了下图所示的蓝色矿井,获得了30克黄金。那么,对于图中的两个灰色矿井,今天你要选择挖哪一个?请圈出你选择的矿井。
![]()
向参与者展示的矿井图
我们希望大多数参与者自动识别以下状态簇(桃黄色和淡紫色的节点分别表示不同的状态簇),并根据脑海里的状态簇决定选择哪个矿井。我们假设,参与者会选择桃黄色的节点而不是淡紫色节点,因为带有标签30、比平均奖励大得多的节点便位于桃红色的状态簇中。
我们Metropolis-within-Gibbs算法进行采访,以接近针对 H 的贝叶斯推断。该方法通过从 H 的后验分布中取样更新了 H 的每个成分,在单一Metropolis-Hasting算法步骤中对所有其他成分进行训练。我们使用了高斯随机游走(Gaussian random walk)作为连续成分的建议分布(proposal distribution),并使用条件CRP先验(conditional CRP prior)作为聚类任务的建议分布[7]。该方法可以定义为一种关于由后验定义的关于效用函数(utility function)的随机爬山算法(stochastic hill climbing)。
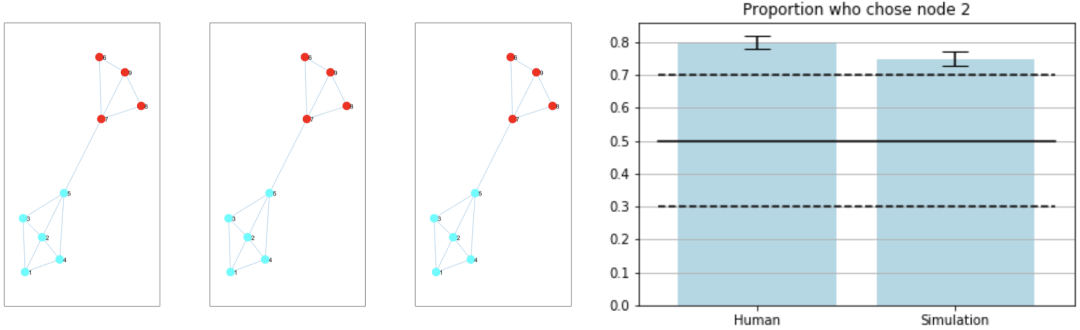
人类组和仿真组中各有32名参与者。前三个状态簇的模型输出结果如下图所示(左侧部分)。前三个结果均相同,表明该模型以高置信度(high confidence)识别出彩色分组。参与者的结果以及静态奖励模型的结果可以从下面的条形图中(右图)看到,此图描述了接下来选择访问节点2的人类和模拟参与者的比例。实心黑线表示平均值,黑色虚线则表示第2.5和第97.5个百分位。
下表中列出的 p 值经右尾二项检验(right-tailed binomial test)计算获得,其中null值在选择左边或右边的灰色节点时被假设为二项分布。显著性水平取0.05,人类实验结果和模型结果均具有统计学意义。
![]()
人类采取的行动及静态奖励模型
奖励催生状态簇
第二个实验的目标是确定奖励是否会催生状态簇。我们预测,即使图结构本身不会催生状态簇,但奖励相同的临近节点也会聚集在一起。
Solway等人的研究发现:
人类更喜欢跨越最少分层边界的路径
[2]。因此,在两条完全相同的路径中做选择时,选中其中一条路径的唯一原因是它跨越了较少分层边界。对此,有些人可能会反驳,认为人们其实更倾向于选择奖励值更高的路径。然而,在接下来详述的设置方法中,智能体只有在实现目标时才能获得奖励,而不是在路径的“行走”过程中积累奖励。此外,奖励值的大小在不同的实验中也有所不同。因此,人们不太可能因为节点的奖励值更高而选择某条路径。
该实验是在网页上进行的,使用了亚马逊土耳其机器人(MTurk)。实验参与者要执行下述任务:
想象你是一名矿工,在由隧道连接的网状金矿中工作。每个矿每天会产出一定数量的黄金(用数值表示)。你的日常工作是从起始矿井导航到目标矿井,并从目标矿井内收集黄金。在某些时间段内,你可以根据喜好自由选择矿井。这时你应该尝试选择黄金数值最高的矿。在另外一些时间段,你只能开采一个金矿,该矿井的黄金数值会被标记为绿色,其他矿井标记为灰色。这时你应该导航到可开采的矿井。每个矿井的黄金数值都会在矿井上作标记,当前矿井将用粗边突出显示。你可以使用箭头键(上、下、左、右)在矿井间导航。到达目标矿井后,你可以按空键来收集黄金数值,周而复始。这个实验将持续100天。
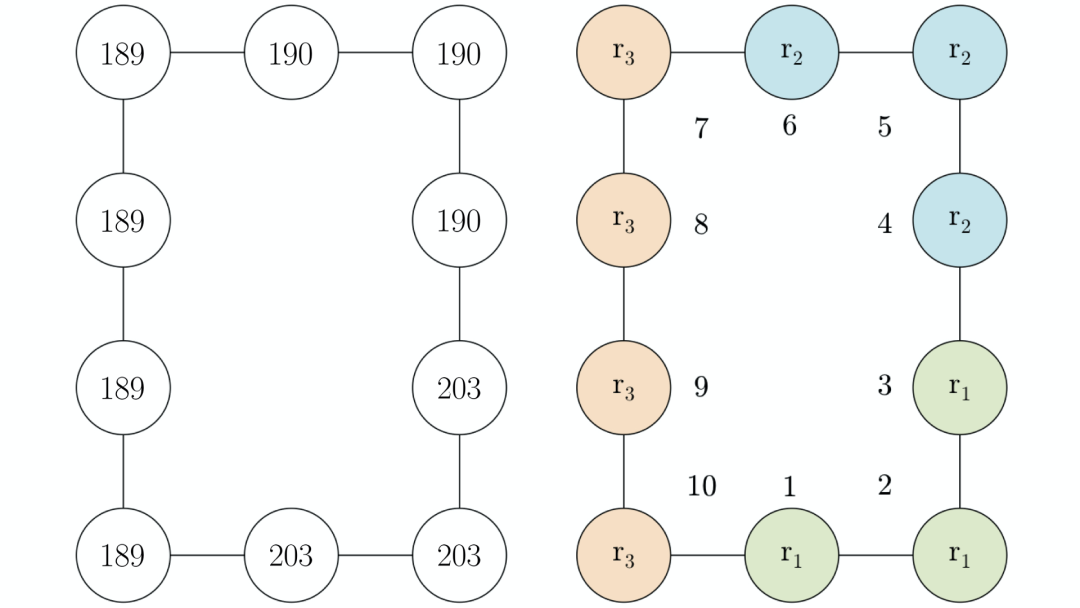
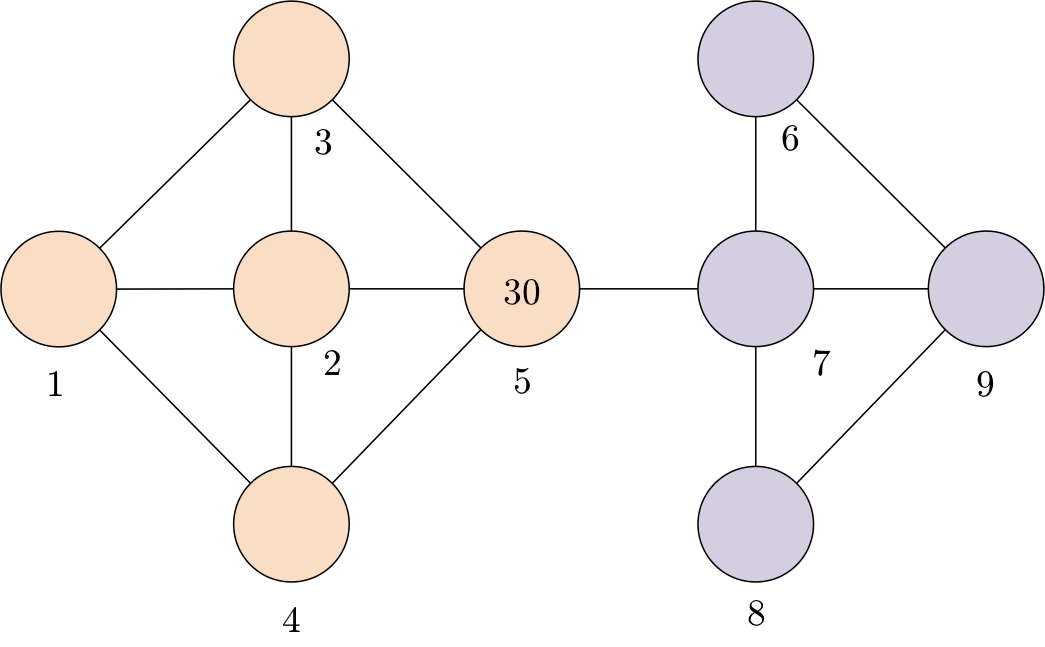
将下图(左侧部分)展现给参与者。与之前的实验一样,为了控制潜在的左右非对称性,我们给参与者随机分配同一图中的布局构造或水平翻转版本,还描述了预期催生出的状态簇,节点编号供参考(右侧部分)。
向MTurk参与者展示的矿井分布图(左)和可能存在的状态簇(右)
我们将第一种情况称为“自由选择”(free-choice),参与者可以自由导航到任何矿井,将第二种情况称为“固定选择”(fixed-choice),参与者需导航至指定矿井。为阻止随机反应,参与者在每次试验中都会得到金钱奖励。
在每次试验中,奖励值的变化概率为0.2,新的奖励值从区间[0,300]中随机抽取。然而,奖励的分组在试验中保持不变:节点1、2和3的奖励值始终只有一个,节点4、5和6的奖励值不同,节点7、8、9和10有第三个奖励值。
前99个试验使参与者能够建立状态簇的层次结构,最后一次试验(以测试试验的形式进行)要求参与者从节点6导航到节点1。假设奖励催生出上面所示的状态簇,我们预测,选择通过节点5的路径的参与者会比选择通过节点7的路径的参与者更多,因为节点5只跨越一个簇边界,而节点7跨越两个簇边界。
我们对固定选择案例进行建模,假设100个试验中的全部任务与提交给参与者的第100个试验(即测试试验)相同。首先,我们提出静态奖励假设,即在所有试验中奖励保持不变。接着,我们又提出动态奖励假设,即每次试验中奖励都会发生变化。
与之前的实验不同,参与者选择一个模型预测的节点,而本实验关注的是,参与者选择的完整路径中,第二个从起始节点到目标节点的节点。因此,为了将模型与人类数据进行比较,我们使用宽度优先搜索算法(breath-first search)的改进形式(以下称为“分层BFS”)来预测从起始节点(节点6)到目标节点(节点1)的路径。
对于每个主体,我们使用Metropolis-within-Gibbs算法从后验样本中进行采样,并选择最可能实现的分层结构,比如后验概率最高的分层结构。然后,我们使用分层的BFS首先在状态簇之间寻找路径,然后在状态簇内的节点之间寻找路径。
我们使用在线推断方法进行动态奖励。对于每个仿真参与者,我们只允许每个试验的取样进行10步。然后,我们保存了分层结构,并添加了经过修改的奖励的信息。接下来,我们从保存的分层结构开始,再次进行采样。在人类实验中,每次试验开始时,尽管状态簇内的奖励值总是相等,但为奖励重新赋值的概率始终为0.2。这种推理方法模拟了人类参与者在许多试验过程中如何累积学习。为了达到此实验目的,我们假设人们一次只能记住一个分层结构,而不是同时更新多个分层结构。我们还修改了对数后验(log posterior),以惩罚非关联的状态簇,因为利用在线推断方法时,非关联的状态簇更加常见。
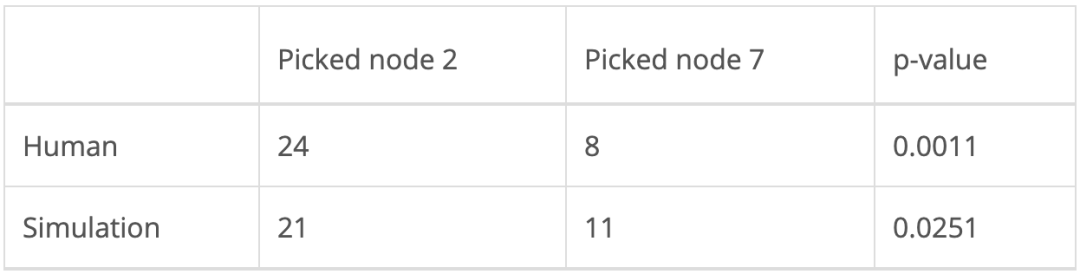
人类组和两个仿真组均有95名参与者。空假设(null hypothesis)由数量相等的参与者选择通过节点5和通过节点7的路径来表示,因为在没有任何其他信息的情况下,假设两条路径的长度相等,参与者选择任意一条路径的概率均为50%。
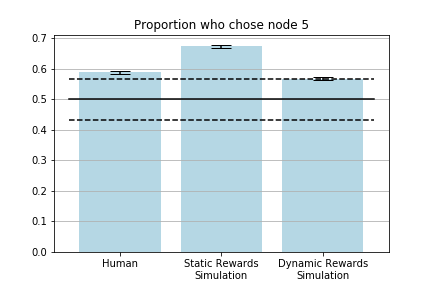
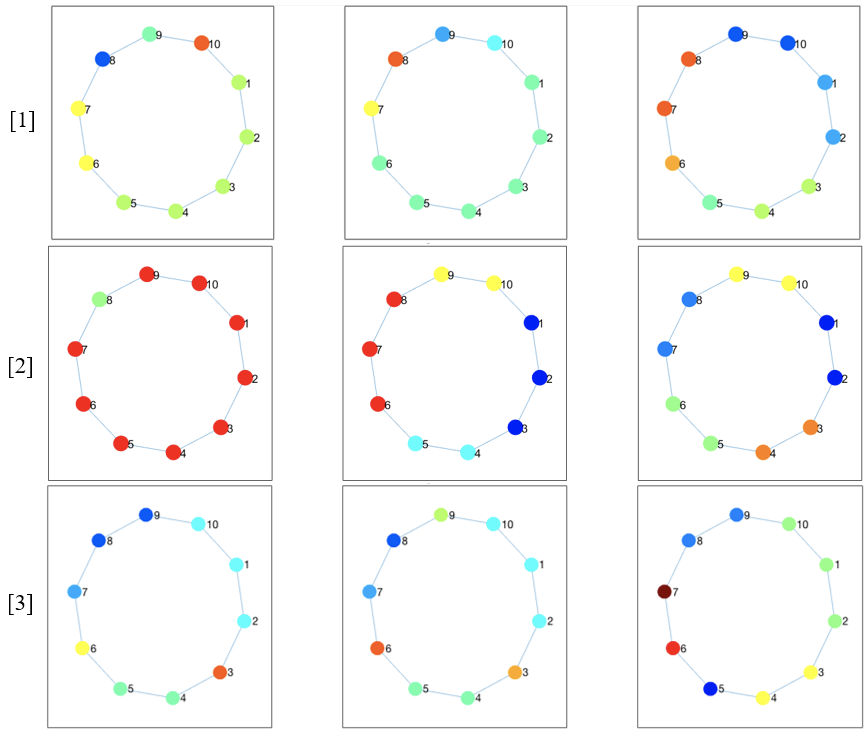
如上表所示,人类实验和静态奖励建模的结果在 α=0.05 时具有重要的统计意义。此外,如下图所示,人体实验的预期结果在以0.5为中心的正态分布的第90百分位处,这也是空假设的预期比例。图中包括由静态奖励模型(第一行)确定的状态簇、可在非关联成分的惩罚项间形成状态簇的静态奖励模型(第二行)以及动态奖励模型(第三行)。
我们使用了Metropolis-within-Gibbs算法的1000迭代生成每个样本,每个样本的可靠性参数和采样间隔均为1。静态奖励下的仿真结果是参与者倾向于通过节点5的路径,达到统计上的显著性水平。此外,由于其目的是对人类行为进行建模,鉴于人类数据在统计学上也具有显著性(0.0321<α=0.05),该结果有意义。
为了模拟人类试验,我们进行了100次试验,每次试验均使用了Metropolis-within-Gibbs算法的10迭代从后验分布中取样。样本的可靠性参数和采样间隔也设置为1。尽管与静态奖励模型下的仿真参与者相比,动态奖励模型下的仿真参与者距离假设更远,但在模拟人类数据方面,在线推理方法似乎比静态奖励建模分析的效果更好。动态奖励模型下,有56名人类参与者和54名仿真参与者选择通过节点5(差异为3.4%),而静态奖励模型下,有64名仿真参与者选择通过节点5,(差异为18.5%)。
上面的柱状图将被选路径的第二个节点是节点5的人类和仿真参与者的比例可视化。黑色实线表示在给定空假设时的预期比例,黑色虚线表示第10和第90个百分位。
结论
人类似乎会自发地将环境处理成支持分层规划的状态簇问题,从而通过将问题分解为不同抽象级别的子问题,将该问题解决。
人们往往是通过这样的分层方式来完成大大小小的任务
,从规划一天的行程、组织一场婚礼到获得博士学位等,往往是“旗开得胜”,第一次尝试就顺利完成任务。
我们谈到,
最优的层次结构不仅取决于图的结构,还取决于环境的可观察特征,
比如奖励的分布。
我们建立了分层的贝叶斯模型来理解状态簇如何催生静态奖励,以及静态和动态奖励如何催生状态簇,并发现,
就我们的模型如何近距离捕获人类行为而言,大多数结果都具有统计学意义
。所有本文呈现的仿真及实验的数据、代码等文件都可以在GitHub的仓库中找到(链接:https://github.com/agnikumar/chunking)。希望本文所介绍的模型可以为将来研究支持分层规划基本认知能力的神经算法提供帮助。
参考链接:
[1] A. Kumar and S. Yagati, Reward Generalization and Reward-Based Hierarchy Discovery for Planning (2018), MIT
[2] A. Solway, C. Diuk, N. Córdova, D. Yee, A. Barto, Y. Niv, and M. Botvinick, Optimal behavioral hierarchy (2014), PLOS Computational Biology
[3] G. Miller, The magic number seven plus or minus two: Some limits on our capacity for processing information (1956), The Psychological Review
[4] G. Roberts and J. Rosenthal, Examples of Adaptive MCMC (2009), Journal of Computational and Graphical Statistics
[5] J. Balaguer, H. Spiers, D. Hassabis, and C. Summerfield, Neural mechanisms of hierarchical planning in a virtual subway network (2016), Neuron
[6] M. Tomov, S. Yagati, A. Kumar, W. Yang, and S. Gershman, Discovery of hierarchical representations for efficient planning (2020), PLOS Computational Biology
[7] R. Neal, Markov Chain Sampling Methods for Dirichlet Process Mixture Models (2000), Journal of Computational and Graphical Statistics
[8] R. Sutton and A. Barto, Reinforcement Learning: An Introduction (2018), The MIT Press
https://towardsdatascience.com/teaching-ai-to-learn-how-humans-plan-efficiently-1d031c8727b
在10月1日头条《秋天的第一本AI书:周志华亲作森林书&贾扬清力荐天池书 | 赠书》留言区留言,谈一谈你对这两本书的看法或有关的学习、竞赛等经历。
AI 科技评论将会在留言区选出15名读者,送出《阿里云天池大赛赛题解析——机器学习篇》10本,《集成学习:基础与算法》5本,每人最多获得其中一本。
活动规则:
1. 在留言区留言,留言点赞最高的前 15 位读者将获得赠书,活动结束后,中奖读者将按照点赞排名由高到低的顺序优先挑选两本书中的其中一本,获得赠书的读者请添加AI科技评论官方微信(aitechreview)。
2. 留言内容会有筛选,例如“选我上去”等内容将不会被筛选,亦不会中奖。
3. 本活动时间为2020年10月1日 - 2020年10月8日(23:00),活动推送内仅允许中奖一次。
![]()
点击阅读原文,直达NeurIPS小组~