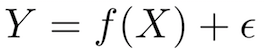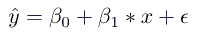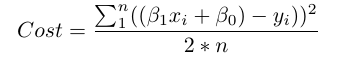《Machine Learning for Humans》第二章：监督学习（一）

作者：Vishal Maini

编译：Bot

如果我们在数字广告上加大投入，最后它会带来多少业绩增长？如果这个人要申请贷款，他是否具备还贷能力？如果你炒股，你预测的明天的股市又是什么样？

对于监督学习问题，我们得先从包含训练样本和相关正确标签的数据集开始。例如，当我们在学习分类手写数字时，如果要用到监督学习算法，我们首先应该收集上千张带有正确数字标签的手写数字图片。然后算法会学着将标签数字和图像一一对应起来，并将学到的经验用于分类从未见过的新图像（不带标签）。这也是智能手机通过扫描拍摄的图片就能识别账单数字的原理。

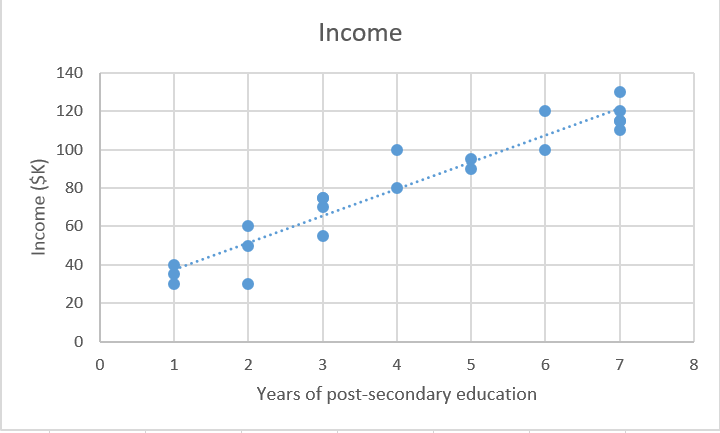
为了说明它是如何实现的，我们可以参考这个问题：根据受高等教育的年数预测个人年收入。简而言之，就是建立一个模型，它能模拟受高等教育年数X和相应年收入Y的关系f。

X（输入） = 受高等教育的年数 Y（输出） = 年收入 f = 描述X和Y之间关系的函数 ϵ (epsilon) = 随机误差项（正/负）

关于epsilon：

（1）ϵ表示模型中的irreducible error。由于噪声影响，算法性能距离理论极限会有一定差距，这个不可约的误差就是ϵ。例如制作一个预测硬币是正是反的模型。

（2）顺便提一点，数学家Paul Erdős把epsilon比作儿童，因为在微积分（不是数据！）中，ϵ表示任意给定的正数ε（不论它多么小）。很贴切不是吗？

预测收入的一种方法是为收入和受高等教育年数构建一个严格的基于规则的模型。例如，受教育的年数每增加一年，相应年收入就提高5000美元。

年收入 = ($5,000 × 受高等教育年数) + 基础年收入 和下文使用的线性回归方法学习解决方案相比，这是一个偏工程的解决方案。

你还可以通过纳入一些其他条件来构建更复杂的模型，如学位类型、工作年限、学校水平等：如果目标获得了学士及以上学位，则将预测的收入值提高1.5倍。

但是这种基于规则的显式编程对于复杂数据并不适用。设想一下，如果你试图写一个由if-then语句构成的图像分类算法，它该怎么从像素角度判断图像上的是不是猫？

监督式机器学习的特点就在于让计算机帮你解决这个问题。通过识别数据中的模式，机器能获得启发。这与人类学习的主要区别在于机器学习在计算机硬件上运行，并且是从计算机科学和统计学的角度总结经验的，而人类的学习模式则发生在生物大脑中（尽管两者目标相同）。

在监督学习中，机器试图通过学习算法运行经标记的训练数据，从零开始学习收入和教育之间的关系。只要我们有受教育年数X作为输入，这个学习算法最终能预测目标的未知年收入Y。换句话说，我们可以将我们的模型用于未经标记的测试数据来估计Y。

监督学习的目标是当给出X已知且Y未知的新例子时，它尽可能准确地预测Y。下面我们主要探讨几种最常用的方法。

监督学习的两个任务：回归和分类

回归：预测连续的数值。这套房子卖多少钱？ 分类：分配标签。这是猫还是狗的照片？

本文将主要讲解回归，在监督学习（二）中，我们再继续讨论分类问题。

回归：预测连续的值

回归预测的是连续的目标变量Y。你可以根据输入数据X来进行估计，如房屋的售价和人的寿命。

这里，目标变量意味着我们想要预测的未知变量，连续意味着Y可以充当的值不存在中断（不连续性），例如，一个人的体重和身高是连续的。另一方面，离散变量只能使用有限数量的值——例如，某人拥有的孩子的数量是离散变量。

预测收入是一个典型的回归问题。你的输入数据X中包含了一些能用来预测未知数值Y的有效信息，如受教育时间、工作经验、工作职位和工作地点。我们把这些线索统称为特征，它可以是数值（如受工作经验），也可以是分类（如职位）。

你需要尽可能多的训练观察数据将这些特征与目标输出Y相关联，以便模型可以学习X和Y之间的关系f。

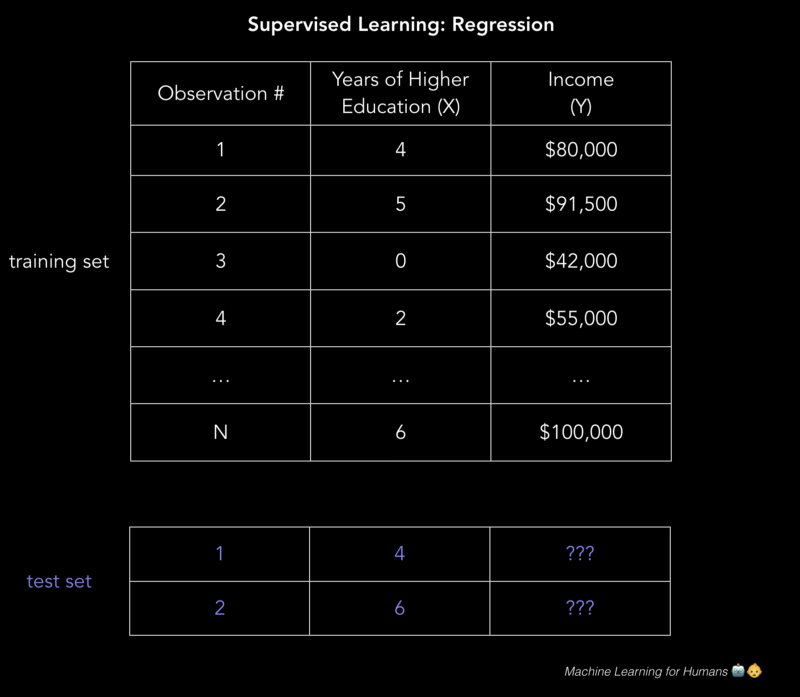
数据被分成训练数据集和测试数据集。训练集有标签，所以你的模型可以从这些标记的例子中学习。训练集没有标签，如你还不知道预测目标的数值。这一过程的关键在于让你的模型能用于预测未知数据的能力，也就是在训练集上表现优秀。

Y = f(X) + ϵ,X = (x1, x2…xn) 训练：机器从标记的训练数据中学习f； 测试：机器从未标记的测试数据中预测Y。 请注意，X可以是任何维数的张量。一维张量是一个向量（1行，许多列），二维张量是一个矩阵（许多行，许多列），所以你也可以有三维、四维、五维……等更多维度的矩阵（如三维张量的三维可以分别是行、列、深）。有关这些术语的介绍，可以阅读线性代数讲义。

对于前文提到的二维收入问题，我们可以用这个.csv文件来建立了解。图中每行包含一个人的教育水平和收入，通过增加表格列数，我们会得到一个更复杂也更准确的模型。

那么，我们该怎么解决这些问题？

一个问题是，我们该如何建立一个模型，使它能在现实世界任务作出准确、有价值的预测？答案是监督学习。

我们先来了解一些有趣的内容：学习算法。我们将探索一些处理回归和分类的方法，并在整个过程中说明关键的机器学习概念。

线性回归（普通最小二乘法）

画一条线。是的，这就是机器学习。

首先，我们将重点先放在用线性回归解决收入预测问题上，因为线性模型在图像识别任务（这是我们稍后要探讨的深度学习领域）中效果不佳。

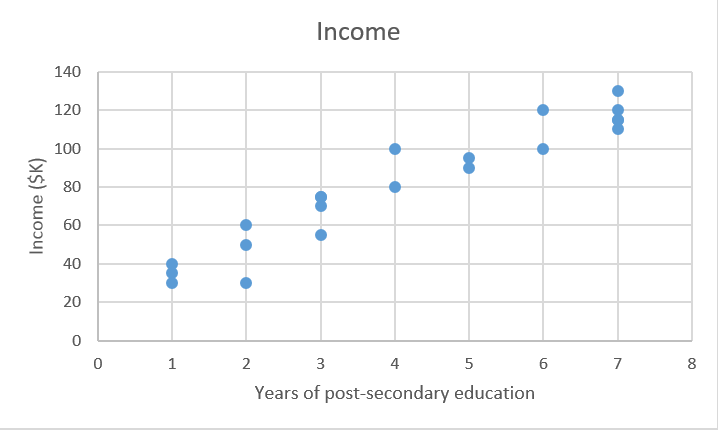
我们有一堆数据X，以及相应目标值Y。普通最小二乘法（OLS）回归的目标是学习一个线性模型，通过使用这个模型，我们可以在误差尽可能小的情况下依靠输入x来预测一个新的y。也就是根据受教育年数预测年收入。

Xtrain = [4，5，0，2，...，6]＃受高等教育年数 Ytrain = [80,91.5,42,55，...，100]＃对应年收入，单位为千美元

线性回归是一种参数方法，这意味着它对与X和Y相关的函数形式进行了假设（我们将在后面介绍非参数方法的例子）。我们的模型将是一个给定特定x预测ŷ的函数：

在这种情况下，我们确定x和y之间存在线性关系——x增加，y会相应增加/减少

β0是y截距，β1是线的斜率，也就是每多一年的教育相应年收入的增减。

我们的目标是学习模型参数（在这种情况下，β0和β1），以最小化模型预测中的误差。

要找到最佳参数：

1.定义一个代价函数，或损失函数，用于衡量模型预测的不准确度。 2.找到最小化损失的参数，即尽可能使我们的模型精确。

从图形上来说，在二维坐标中，这会产生一条最适合的线。在三维中，我们将绘制一个平面，以此类推，在更高维数的空间中，我们会得到一个超平面。

关于维度的说明：为简单起见，我们的示例是二维的，但你的模型中通常会包含更多特征（x）和系数（β），例如添加更多相关变量以提高模型预测的准确性。尽管可视化难度会更高，相同的原则可以推广到更高的维度。

在数学上，我们计算每个实际数据点（y）和我们模型的预测（ŷ）之间的差。再对这些差做平方以避免出现负数，同时惩罚较大的差异，然后将它们相加并取平均值。这是衡量我们的数据如何符合要求的指标。

对于这样一个简单的问题，我们用微积分就能算出一个能使损失函数最小化的最佳β参数。但随着代价函数/损失函数越来越复杂，这种微积分的方法就不再适用了。这时，我们可以考虑使用一种能最小化损失函数的方法——梯度下降。

相关阅读：《Machine Learning for Humans》第一章：为什么机器学习至关重要