Nature Com.:自发对称性破缺 与嵌段共聚物自组装

海归学者发起的公益学术平台

分享信息，整合资源

交流学术，偶尔风月

Nature Communications今日在线刊登了麻省理工学院材料系的Alexander-Katz课题组关于软物质自组装的工作。他们发现嵌段共聚物在模板中会自发组装为长周期性的超晶格结构，这一发现是自发对称性破缺在软物质领域的一个有趣例子。

在介绍自发对称性破缺的定义前，我们先来看一个有趣的问题：如何修一条最短的路，可以连接正方形四角的房子？

我们的直觉可能告诉我们，把对角线相连。但是如果计算一下的话，我们可以看到这并不是最优解。

最优解是如下图所示的情况：

直觉上讲，我们可能会疑惑，为什么一个四重对称的问题，会有一个二重对称的解？其实自发对称性破缺的核心在于，每个单独的解无法保持系统的高对称性，但是所有解法的集合使我们重新获得原体系的对称性。具体到修路的问题，其两个最优解是：

自发对称性破缺是与相变，简并量子态，希格斯机制等许多物理过程相关的基本现象。本工作是软物质自组装领域的自发对称性破缺的一个例子。

嵌段共聚物是一类非常重要的软物质。在分子水平上，灵活的碳 - 碳单键和 sp3 杂化允许各种构型的变换，使碳链能够像绳索一样缠绕运动。两种不同的碳链通过一个（或多个）共价键相连，使嵌段共聚物在纳米尺度下会形成自组装结构。之前的工作中，人们可以直接通过嵌段共聚物自组装在表面实现复杂的二维介孔结构。而进一步配合光刻产生的模板，自组装可以实现超高分辨率（低于 10 纳米）超高复杂度的各种结构，从而被用于高精度纳米加工中。

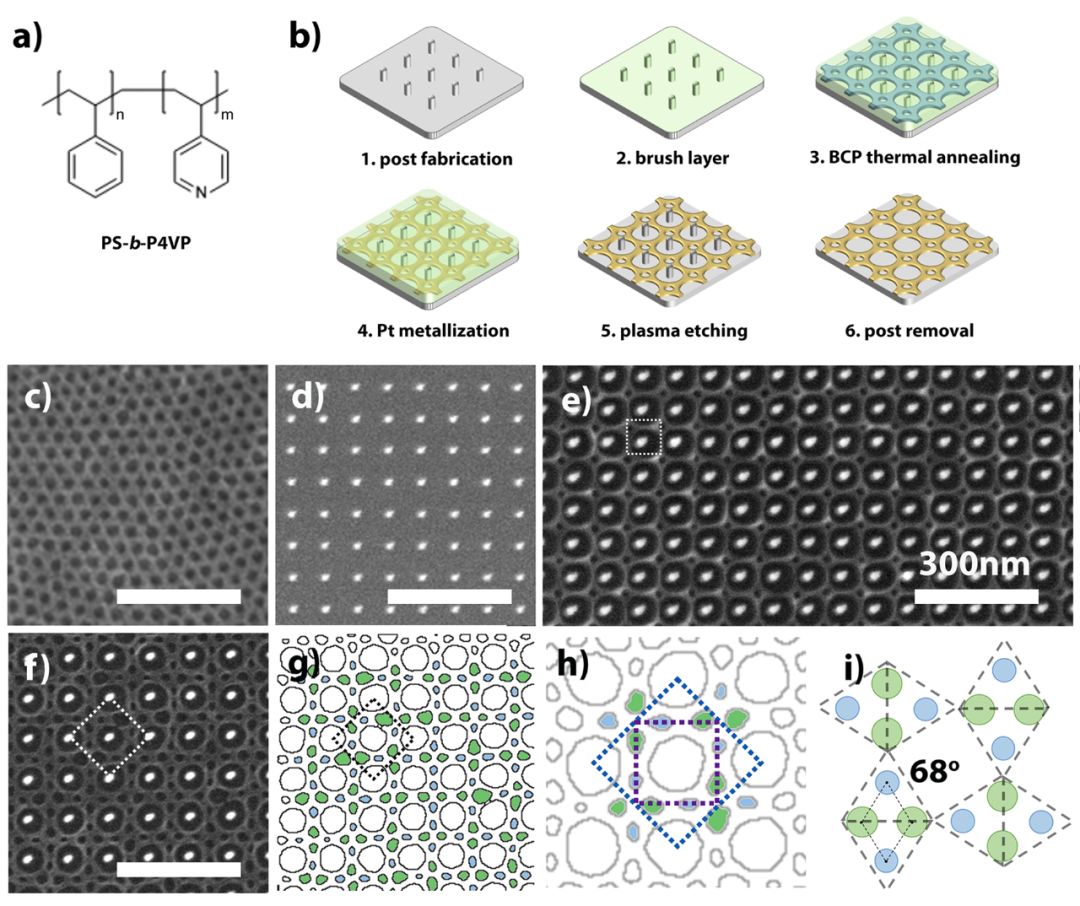
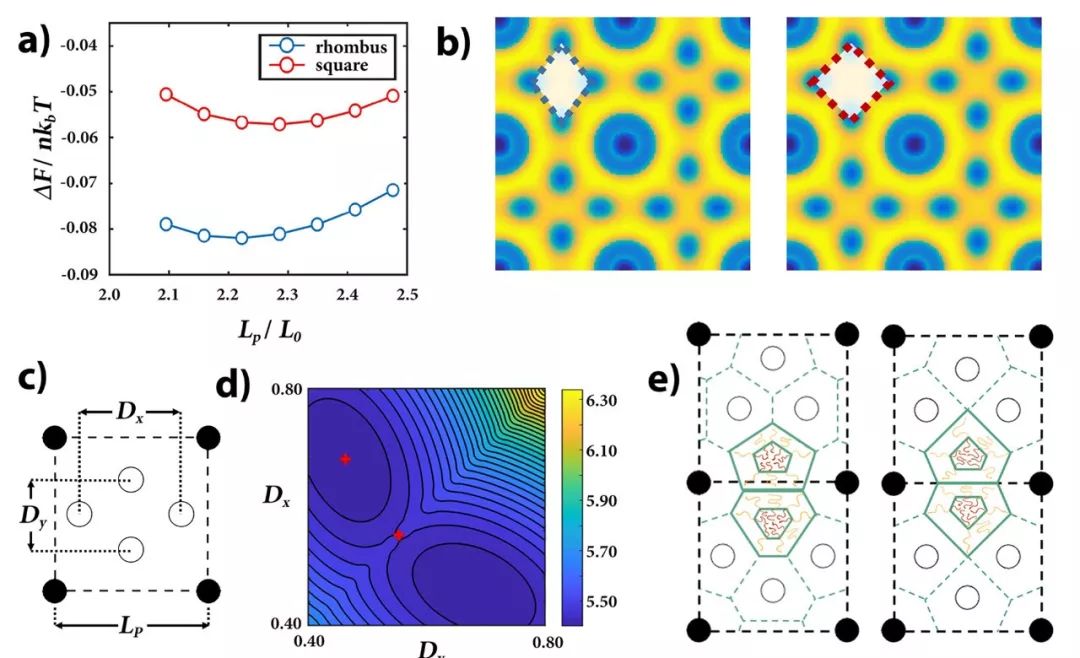
本工作试图了解嵌段共聚物的自发对称性与模板对称性不匹配时，会发生什么现象。研究人员将嵌段共聚物放入由直立柱（直径约 10nm，高度约 40nm）组成的正方形阵列模板中，并观察它们如何相应地调整其组装行为（图 1a – b）。

图 1

之前的工作认为，嵌段共聚物作为软物质，会遵循模板的对称性。而当对称性不匹配产生的应力过大时，体系会产生缺陷。然而本文发现在具有正方对称的模板（图 1d - f 中的白点，空间群p4mm）内部，嵌段共聚物结构（图 1g – i 中的蓝点和绿点）非常有序地组成二重对称结构（空间群 p4gm）。而这些二重对称结构又进一步组成超晶格结构（图 1g – i）。

通过理论模型和自洽场模拟可以完全理解了这种自发对称性破缺的原因。本质上讲，这种对称性的降低是由熵和焓之间的权衡驱动的。熵贡献来自聚合物分子构型，而焓贡献来自二嵌段界面。只有采用这种低对称超晶格几何结构，嵌段共聚物才能使系统的自由能最小化（图 2a 对比了图 2b自洽场模拟结果中，高对称与低对称结构的自由能关系，图 2c-d 是理论模型结果，图 2e 体现了聚合物构型对熵和晗的贡献）。

图 2

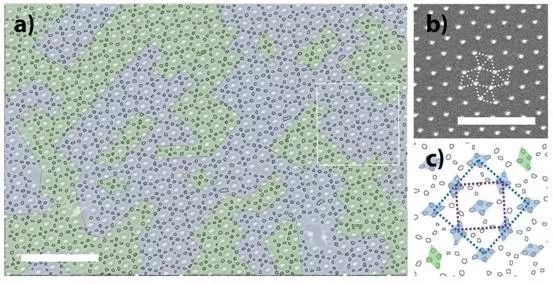
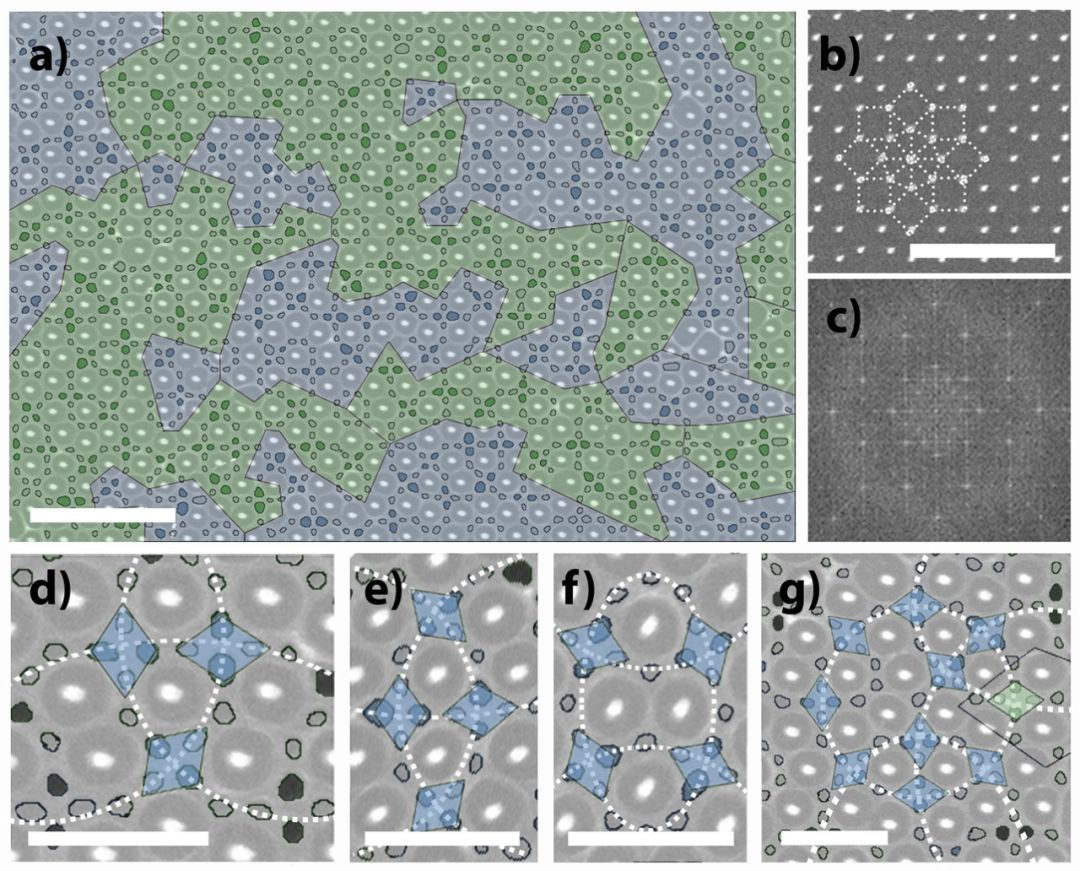
进一步，文章又将这一发现应用于更复杂的对称体系（图 3 为 32434 Archimedean tilings， 图 4 为二维准晶 Ammann-Beenker 等），并证明这一嵌段共聚物的自发对称性破缺现象在其他复杂对称体系中普遍存在。

图 3

图 4

从科学角度，这是一个可以看到的自发对称性破缺的有趣例子。从技术角度，这一发现揭示了嵌段共聚物自组装作为微纳米加工技术的潜力和局限性：我们一方面可以通过设计模板来实现新的表面结构和更高的分辨率；而另一方面， 应该时刻注意实现的结构是否可以保持模板原有的结构与对称性。本工作可以为其他自组装领域的研究者提供新的思路与视角。

该项工作由麻省理工学院材料系Yi Ding, Karim R. Gadelrab, Katherine Mizrahi Rodriguez, Hejin Huang, Caroline A. Ross, Alfredo Alexander-Katz共同完成。

点击左下角阅读原文。

扩展阅读

 

中国团队自组装拓扑保护铁电纳米岛,调控畴壁电导

北大发现三维拓扑狄拉克半金属中的非常规超导特性

当拓扑已成家常 | Ising专栏

祁晓亮: 我的拓扑绝缘体之路

对称破裂：层状钙钛矿负热膨胀的原因

本文系网易新闻·网易号“各有态度”特色内容

媒体转载联系授权请看下方