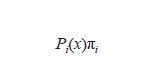贝叶斯关于概率和统计学的思考

下文摘自《10堂极简概率课》, [遇见] 已获授权许可, 特此表示感谢. 

从贝叶斯到菲尼蒂再到本书作者，贝叶斯学派的所有人都认为概率和统计学是同一学科的不同组成部分。比如，菲尼蒂给他的著作取名《概率、归纳和统计学》（Probability, Induction and Statistics）。但并非所有人都同意这个观点，一大批统计学家认为统计学是一个独立学科，需要有它自己的基础。

贝叶斯( Thomas Bayes）

“概率是数学的组成部分。”在一个典型的概率问题中，我们知道某个集合中的x 概率赋值P(x)，还知道结果的子集A。我们需要根据这些已知信息，计算或近似计算P(A) 的值，即与A中所有x 对应的P(x) 的总和。由于x 属于一个大集合，A 可能非常复杂（大家可以回想一下生日问题），因此有的概率问题极富挑战性，在长达400多年的时间里让众多最优秀的数学家头疼不已。

“统计学是概率的对立面。”在一个典型的统计学问题中，我们知道概率分布族P = {P1, P2, …}，并且知道从其中一组概率分布中抽取的x，我们需要猜测或估算Pix 是从哪里抽取出来的。

贝叶斯的伟大思想是，通过给不同的概率分布Pi指定一个先验分布πi，使统计学成为概率的一个组成部分。根据贝叶斯定理，在x被观测到之后，与不同的i 对应的后验概率和

之间存在比例关系。因此，我们可以选择最大后验概率对应的i（或者使某个平均损失最小化的i）。

问题在于，贝叶斯必须指定πi，即使对生日问题来说，这也是有难度的。生日在可能结果中的分布真的均匀吗？要不要考虑周末效应呢？（周末的人口出生率比工作日低20%。）要不要考虑季节性影响呢？如果你知道这些知识，你的先验就应该有所体现。

不指定先验就进行统计的相关统计学文献非常多。统计学领域的“爱因斯坦”费希尔提出了最大似然法：选择使观测数据最有可能出现［Pi(x) 值最大］的i。在πi均匀（不受i影响）时，该方法与贝叶斯法则没有区别。当下有很多人在研究“客观贝叶斯分析”，试图将这种对应关系推广至更具现实意义的无限空间问题。

罗纳德·艾尔默·费希尔(Ronald Aylmer Fisher, R. A. Fisher）

与此同时，还出现了许多不同于贝叶斯的选择i的方法，包括最小方差估计、无偏估计、卡方检验、极小化极大估计、极大化极小估计……

每种方法都有其对应的贝叶斯分析：如何假设先验分布，非贝叶斯估计才会切合实际？这个问题有时会引发矛盾，因为贝叶斯估计都不是无偏估计。相关讨论引出了一条迷人的定理，其提出者亚伯拉罕·瓦尔德和查尔斯·斯坦（Charles Stein）是反贝叶斯主义的坚定者，就连他们也为该定理感到震惊。

亚伯拉罕·瓦尔德（Abraham Wald）

这条定理认为，粗略地说，任何合理的估计量都是某种贝叶斯先验。生物统计学家杰罗姆·科恩菲尔德（Jerome Cornfi eld）因此断言：

贝叶斯观点可以用一句话概括：任何不遵循某个似然函数和某些先验的推断或决策过程，都存在客观的、可证实的缺陷。更粗略地说，任何不愚蠢的统计程序都符合贝叶斯定理。

这并不意味着贝叶斯分析总是容易的。我们以抛掷一枚真实的图钉为例。如果图钉落地后针尖朝上，则计1；如果它落地后针尖指向地面，则计0。

在经典的贝叶斯分析中，θ 表示单次抛掷后针尖朝上的概率，它是未知的。假设θ 的先验是均匀的，图钉已被抛掷了10次，而且从未出现针尖朝上的结果。那么，在接下来的10次抛掷中，不会出现针尖朝上的结果的概率是多少？经典计算表明，这个概率大约为1/2（11/21）。假设把数字10换成n 。在n 次实验未取得成功的情况下，接下来的n 次实验也不会成功的概率是多少？无论之前未成功实验的次数是多少，答案同样约为1/2，即(n + 1)/(2n + 1)。如果这个答案在令我们吃惊之余还让我们感到失望，就说明我们假设的均匀先验可能是存疑的。

这个答案让哈罗德·杰弗里斯（Harold Jeffreys）和多萝西·林奇（Dorothy Wrinch）忧心忡忡，为此他们尝试了各种各样的先验。他们建议为0 和1这两个位置分别赋予某个先验概率质量。如果赋予0的先验概率是1/3，赋予1的先验概率是1/3，而且两者之间的概率是均匀的，那么在已知前10次失败的情况下，接下来失败10次的概率超过90%。

欧文·古德（Irving Good，与图灵合作，破译了恩尼格码）称这是一种典型的虚构结果策略。即使没有真的抛掷图钉，嵌在计算过程中的思想实验也表明均匀先验可能是不恰当的！一些关于贝叶斯定理稳健性的文献研究了先验变化对结论的影响，对我们有启迪作用。

如前所述，贝叶斯定理的基本框架简单明了，具有相容性，但实际应用过程却复杂得多。

戴维·考克斯（David Cox）在他的《统计推断原理》（Principles of Statistical Inference）中对此进行了翔实的描述，值得一读。建立有效模型的准备工作通常被称为探索性数据分析，有其自身的理论基础。

实际操作的复杂性使我们想起了阿莫斯·特沃斯基说过的一句话：“即使有统计数据，你也可能会撒谎；但没有统计数据的话，撒起谎来就会容易得多。”(本节完)

作者： [美]佩尔西·戴康尼斯（PersiDiaconis）

          [美]布赖恩·斯科姆斯（Brian Skyrms）

美国斯坦福大学最受欢迎的概率课

从抛硬币到量子物理，

他们讲清楚了概率这个困扰众多学术大咖几个世纪的问题。

在16世纪和17世纪，赌博玩家和数学家把随机性从一个难解之谜变成了概率论，在诸多领域中引发了一系列变化和突破，从赌博、数学、统计学、经济学、金融到物理学和计算机科学。这本书讲述了关于概率的10个伟大思想背后的故事：是谁构建了这些伟大的思想？这些思想的哲学意义和应用价值体现在哪些方面？