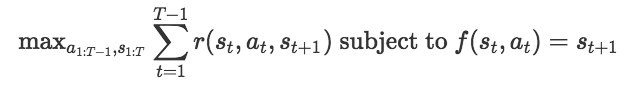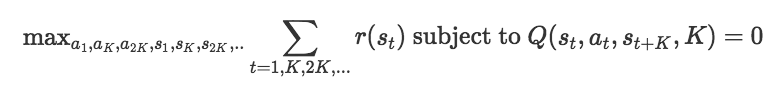TDM：从无模型到基于模型的深度强化学习方法

来源：arXiv

编译：Bing

编者按：当人类学习一项新技能，往往是不断试错与计划的交织，机器也是如此。强化学习有基于模型的方法和无模型的方法，那么如何将二者联系起来呢？加州大学伯克利分校的研究人员分发表论文，介绍了一种新的TDM方法，实现了从无模型到基于模型的过渡。以下是论智对原文的编译。

假如你想从你位于UC Berkeley的家骑车到金门大桥，路程有20英里，但是问题是：你从来没骑过自行车，更糟糕的是，你第一次来湾区，只有一张地图，这该如何开始呢？

首先我们先想想如何骑自行车。一个方法是大量地学习并做计划，读一些学骑自行车的书，学习物理学和解剖学，详细制定出针对车子的每个扭动该用哪快肌肉。这种方法很新奇，但是对于任何一个学过骑自行车的人来说，这种方法绝对会失败。学习骑车只有一种方法：试错。这类任务一般都比较复杂，无法在脑海中制定详细的计划。

一旦你学会了骑自行车，接下来要怎样到达金门大桥呢？这里依然可以用试错法，多转几个弯，看最终是否能到金门大桥。但是这种方法要花很长时间。对于这类问题，做计划是更快的策略，并且不需要太多的现实世界的经验和试错。在强化学习术语中，它更具有样本效率。

用试错法学到的技能

有些时候，提前做计划更好

虽然简单，这一案例说明了人类智慧中的重要部分。对于某些任务，我们使用试错法，而对于另一些任务，我们用计划法。这种情况也同样出现在强化学习中。在强化学习术语中，实证结果表明，某些任务更适合无模型的方法（试错法），有些更适合基于模型的方法（计划法）。

但是，骑自行车的案例也说明，这两个系统并不完全独立。特别是学自行车只需要试错的说法是过于简单了。事实上，当你在用试错法学骑自行车时，也会加点计划。也许刚开始，你计划的是：“不要摔倒。”随着技术的提升，你的计划变成了：“往前走两米，并且不摔倒。”最后，你的骑车的技术非常熟练了，以至于可以指定非常详细的计划：“骑到路的尽头。”在这之后，计划就是工作的主要内容了，你无需担心技术问题。我们可以看到，在这学骑自行车的活动中，我们从无模型的试错法逐渐过渡到基于模型的计划战略中。如果我们可以开发模拟这种行为的人工智能算法，特别是强化学习算法，它可以生成一种算法，让两种方法都能很好地进行，并且对样本很高效。

本文介绍了一种时间差分模型（temporal difference model，TDM），它是一种强化学习算法，可以在无模型和基于模型的强化学习算法中进行平滑过渡。在介绍TDM之前，我们首先介绍一下传统基于模型的强化学习算法是如何工作的。

基于模型的强化学习

在强化学习中，我们有状态空间S和动作空间A。如果在某一时刻t时，我们处于状态S_t∈S，并做出动作a_t∈A，我们就通过动态模型f:S×A→S转换为一个新状态s_t+1=f(s_t, a_t)。这一步的目标是将visited状态的的奖励最大化。基于模型的强化学习算法假设你已有（或学习了）动态模型f。有了这个动态模型，就有许多可用的基于模型算法。在这片文章中，我们用以下优化，选择一系列动作和状态来使奖励最大化：

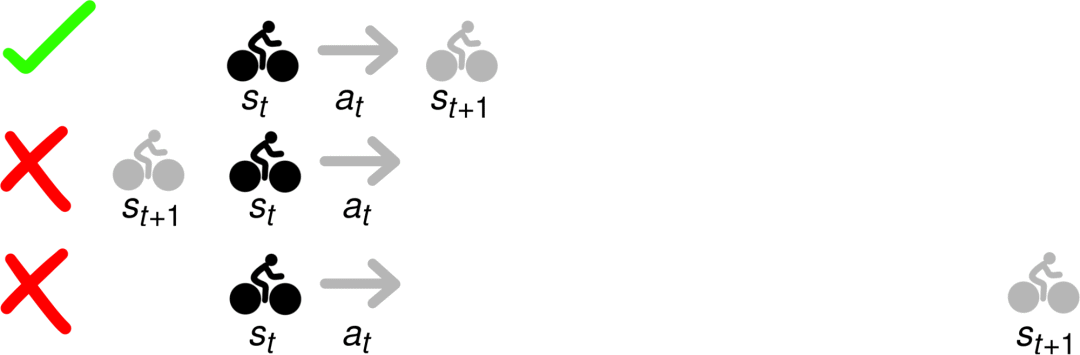
优化在选择可以使奖励最大化的状态和动作的同时，还要保证路线是可行的。这里的“可行”表示每个阶段的过度是合理的。例如，在下图中，如果你从状态st开始，采用at动作，只有最上方的st+1才能表示可行的过度。

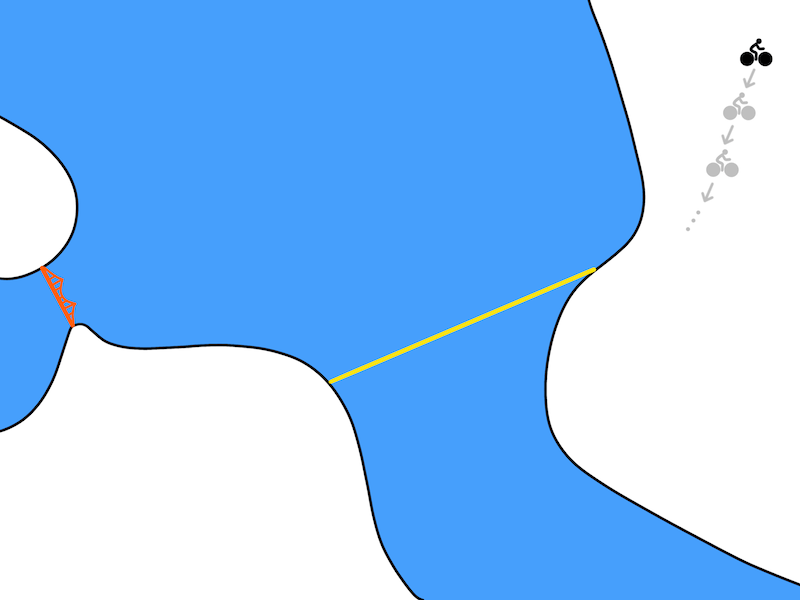
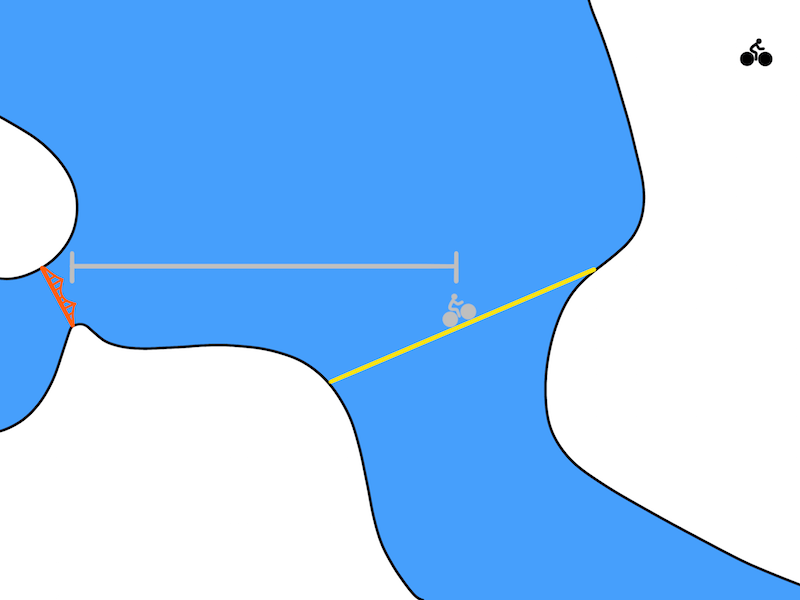
在我们骑自行车的问题中，优化方法可能会提出下图的解决方案，右上角是从Berkeley出发，图中左部是金门大桥：

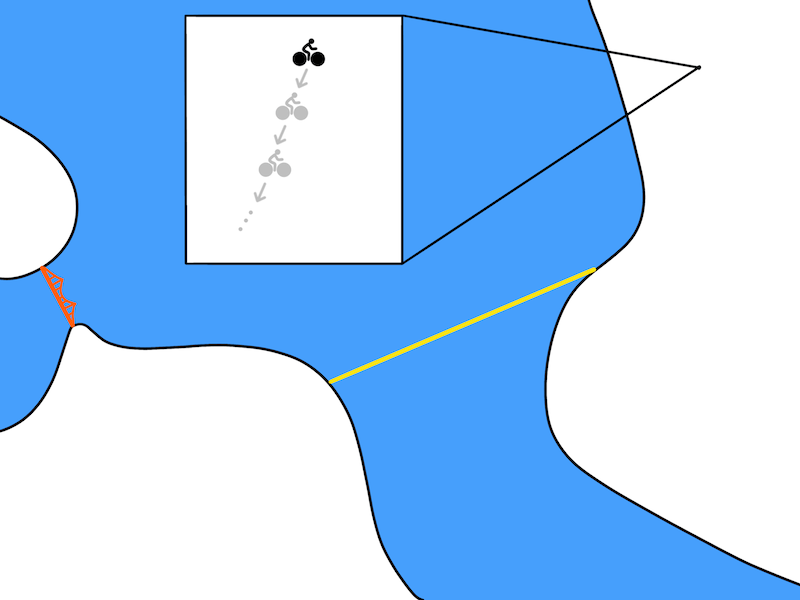
尽管理论上没问题，但是这个计划不太切合实际。基于模型的方法利用模型f(s, a)预测要进行下一个时间段的状态。在机器人领域，一个时间段通常对应的是十分之一秒或百分之一秒。所以一个更实际的解决方案看起来应该是这样：

如果我们思考一下每天做的计划，就会发现我们计划了许多在时间上很抽象的条目。与其计划我们的自行车在下一个十分之一秒后在哪，不如做个长期计划，比如：”我要走到路的尽头。“甚至我们能在刚一学会骑自行车的时候就能做出这些时间抽象的计划。正如之前讨论的，我们需要一些方法：

1. 利用试错法开始学习；

2. 提供一个机制，可以逐渐提高我们用于计划的抽象水平。

对于这一点，我们引入了时间差分模型。

时间差分模型（TDM）

我们将该模型用Q(s, a, s_g, τ）表示，其中s∈S，表示状态；a∈A，表示动作；s_g∈S，表示目标状态，它们用来预计智能体到达目标位置需要多少个时间段τ。通俗点说，TDM是用来回答：“如果我要在30分钟内骑自行车去旧金山，这段时间我能走多远？”对于机器人，用来测量距离的常用方法是欧氏距离。

对于这些类似强化学习的方法，TDM可以看做是有限时域MDP中的目标条件Q函数。因为一个TDM就是另一个Q函数，我们可以用无模型算法训练它。我们用深度决策策略梯度（DDPG）训练TDM，然后对目标和时域进行反向打标签，以增加我们学习算法的样本效率。理论上，任何Q学习算法都能用来训练TDM。具体细节可阅读原论文。

用TDM做计划

当我们训练好TDM后，怎么用它来做计划？最终研究人员得出以下优化：

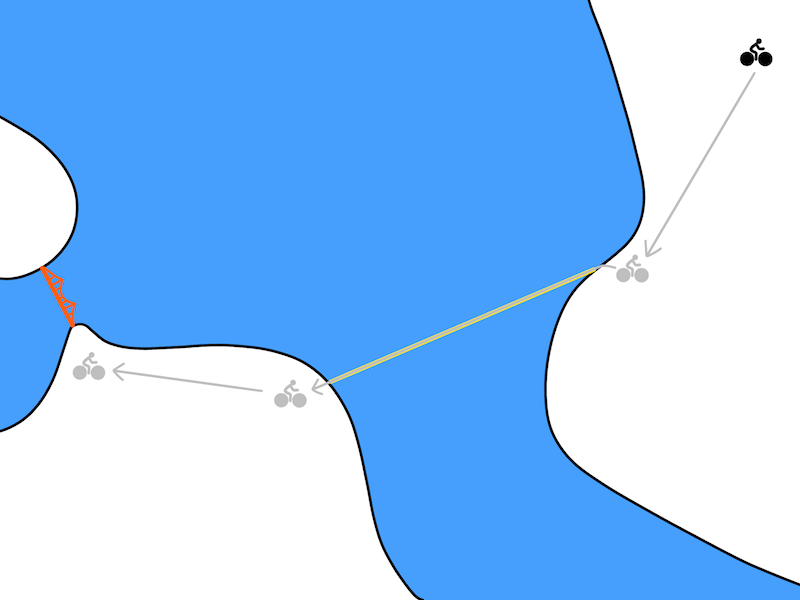
这和基于模型的公式很像，选择一组能使奖励最大化的行为和状态就能应用到上面公式。唯一的区别是我们只需要计划每K个时间段就可以，无需计划每个时间段。其中，Q(s_t, a_t, s_t+k，K）=0的限制能让路线绝对可行。用图像表示出来，即：

每个时间段都做计划

每K个时间段做一次计划

随着K的增加，我们的计划也越来越抽象。在K个步骤之间，我们用无模型的方法做动作，这样一来，无模型的策略就能把到目标的距离“抽象化”。在自行车问题中，当K足够大时，结果可能如下：

需要注意的是，这个公式只能在每K个步骤中优化奖励。然而，许多任务只关心某些状态，例如最终是否到达金门大桥，所以我们需要注意各个任务的目的。

实验

我们在五个模拟连续控制任务和一个真实的机器人任务上测试了TDM。其中一个模拟任务是训练机械臂，让其将圆柱体推到指定位置。下面显示了TDM最终的推动策略，以及学习曲线：

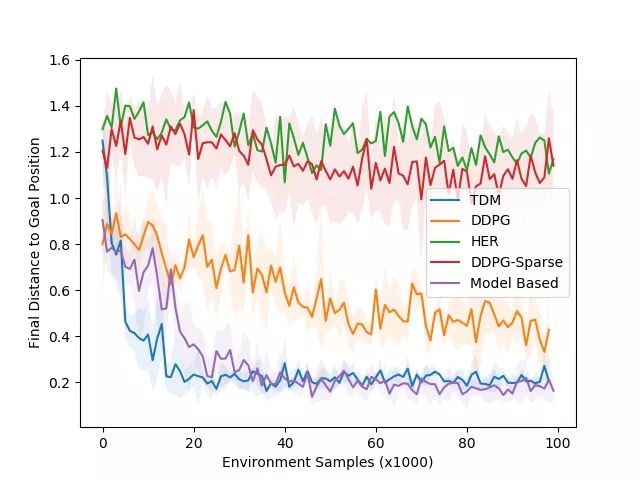
在下方的学习曲线中，我们绘制了到目标的最终距离与环境样本的数量（越低越好）。我们的模拟器用20Hz控制机器人，说明1000个时间段相当于现实世界的50秒。这种环境相对更容易学习，说明基于模型的方法很不错。和预期的一样，基于模型的方法（紫色曲线）学习的速度很快，用时约3000个时间段（或现实中的25分钟），并且表现良好。TDM方法（蓝色曲线）也能快速学习，大约用了2000个时间段（或现实中的17分钟）。无模型的DDPG（没有TDM）基准最终解决了这一任务，但需要更多的训练样本。TDM方法能如此迅速地学习的一个原因是，它实际上是一种伪装的基于模型的方法。

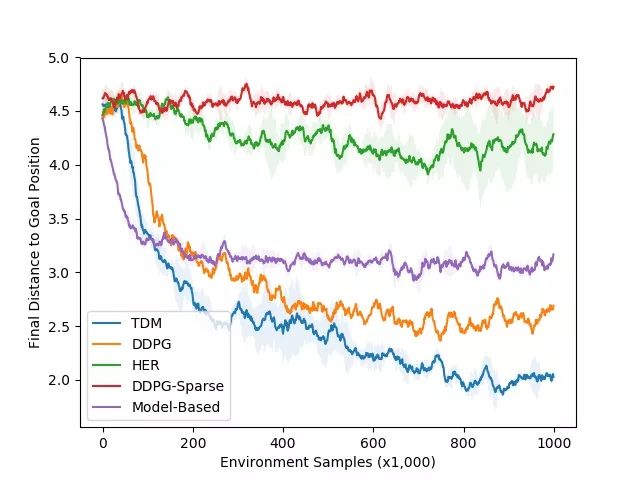
当我们将任务变为运动时，无模型方法的表现就好多了，其中涉及的动作更复杂。其中一项运动任务是训练一个四足机器人移动到某个位置，下图是TDM的结果及学习曲线：

正如我们使用的试错法，而不是计划法学会骑自行车一样，我们希望无模型的方法能在这些任务上比基于模型的方法表现得更好。这正是我们在右边的学习曲线中看到的：基于模型的方法在性能上保持平稳。无模型DDPG方法学习速度更慢，但最终由于基于模型的方法。TDM能快速学习并保持最佳性能。

未来展望

时序差分模型为无模型向有模型控制的过度提供了形式化和使用的算法。基于此，未来还有很多工作需要解决。首先，要思考如果环境和策略是确定的该如何。实际上，大多数环境是随机的，即使他们是确定的，在实践中使用随机策略也是有道理的。将TDM扩展到如此设置上将有助于其在真实环境中工作。另外，就是将TDM与其他基于模型的计划优化算法相结合。最后，我们希望将TDM应用到真实的机器人身上，完成更具挑战性的任务。

论文地址：arxiv.org/abs/1802.09081

代码地址：github.com/vitchyr/rlkit