娃才上一年级,让你怀疑人生的数学题已经来了
以下的提问,来自一个自信快乐的一年级小女生的妈妈。小屁孩儿,这个词说出来其实带着作者深深的爱怜。
“娃一年级下了,学到了100以内加减法运算。随之,最近产生了一种情景数学题:A给了B 8颗糖,给完后AB的糖一样多,问:给糖之前,A的糖比B多了多少颗?
我先按事件时间轴倒叙法,教娃往回推,理解不了;后来拿出了一堆核桃,一对一摆两排,直观地摆来摆去,还是有点懵;
再后来,我把题中的数字改为到1、2,孩子似乎理解了。但是,换个5以上的大数字,或者换个问法,孩子又懵了。
我的想法和疑问是:不是孩子笨,而是7岁出头的孩子的抽象思维跟不上,所以她没法从这个情景中提炼出规律来。是么?”
嗯,是的。孩子不笨。题目有问题。
题目难在哪儿?
这题,其实还真挺难的。先是A和B两个字母就看着扎眼睛:什么什么嘛,张小明李小红都哪儿去了?
更重要的,难就难在题目中A和B的糖的数量可以是任何自然数,恒定的只是他们之间的差异。这个,估计让很多小屁孩儿都感觉百爪挠心,一万种不舒服。当然啦,你们成年人管这种不舒服叫逆向思维。
小屁孩儿读这道题是什么感受?
来,我给你们翻译一下:
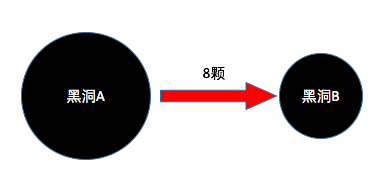
一个黑洞给了另一个黑洞8颗糖,然后两个黑洞就一样大了,然后大黑洞比小黑洞大多少呢,然后就好多好多黑洞洞….
我还特地画了个非常不精确的示意图,麻烦你发挥想象力感受一下。
对于小屁孩儿来说,他们特别习惯于 “张小明有20块糖,李小红有4块糖,张小明给了李小红8块糖之后,两个人各自还有几块糖啊?” 行为检点的应用题不都应该是这样的么?
所以啊,敲黑板总结一下难点:
1. 字面上,“A”和“B”的说法很可能增加了孩子的认知负荷,换成具体人名字会更好 ;
2. 数量A和B本身具有不确定性,这一点对于还在理解数字和数量的对应关系的孩子来说是有困难的,这应该是这道题最大的难点;
3. 当数量A和B不确定的时候,它们之间的差异(difference)却是确定的, 这其中其实已经体现出了代数的思维。
家长往往这样做
当你把A和B分别冠名,成了张小明李小红之后,孩子仍然一脸懵圈,这个时候你还应该做些什么呢?
第一类家长:用核桃!
先表扬这些家长! 用具体实物帮助孩子学数学的重要性那是大的很。核桃,花生,瓜子儿,大米都行,摆来摆去也没问题,但是别忘了,孩子心理总是过不去那个坎儿——张小明和李小红, 他们每个人到底有多少颗糖啊!
所以这个时候,你不妨给出固定数量,帮孩子填上那个巨大的黑洞:
比如张小明有18颗糖,给了李小红8块,然后俩人糖就一样多了,这时候张小明和李小红应该各自有多少糖?那么李小红原先应该有多少颗糖?
再比如张小明有20颗糖,这回呢?
再再比如,张小明发财了,他这次有30颗糖,这回呢?
然后,就到了我们去发现规律的时间……
问问孩子,每一种情况,张小明都比李小红多了多少块糖?这个数字会一直是16么?为什么?
通过上面的比如,再比如,再再比如中的具体数字代入之后,能不能完成从具体到抽象的升华,全靠这一问了。
第二类家长:画图
画图的确是个好办法,但是在你动笔之前,你确定你想清楚了这图该怎么画?
比如,A和B是画成圆圈呢,还是画成线段? 或者你也在懵圈中:A和B的数量不是不确定么,这图能画么?
如果你画图的目的是想帮助小屁孩拨云现日,那这张图至少要满足两点要求:
1. 能够把题目中的数量关系简化;
2. 孩子要能够认可你的这种画图方式;换句话说,你为什么画圆圈,或者为什么画线段,圆圈或者线段又怎么能代表糖块? 这些,你必须取得小屁孩儿的首肯,不然图画了白画。
所以,请你想想看,张小明李小红分糖豆儿这个图你打算怎么画?
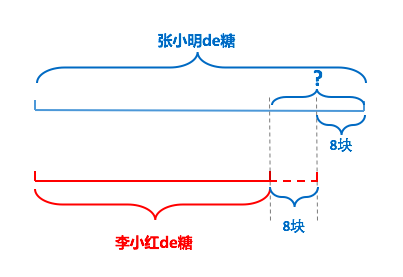
有关数量的比较,我的建议是,线段是个好方法。比如下图,连张小明和李小红分别用什么颜色表示都需要小心点(不是吓唬人,这个完全从符号学的角度说)。当然,祝你找到更好的图解方式,也别忘了分享给我们。
至于那些上来就列方程 X-8=Y+8,所以 X-Y=16的家长,请你务必控制你寄几!
孩子的大脑吃得消吗?
皮亚杰,当代著名的儿童发展心理学家,把儿童的天然认知过程分成了4个阶段。
简单粗暴的说来,这就是孩子大脑的CPU从组装到出厂的4个阶段:
1
感知运动阶段(Sensorimotor Stage):0-2岁
在这个阶段,小屁孩主要通过感官,包括听觉、视觉、触觉和味觉来感受世界。他们对这个世界的理解完全依赖于他们和周围环境的互动。
这个阶段,屁孩儿开始明白物体恒在,即使绒布兔子被藏在了门后面,他们也开始知道,兔子还在,世界还没有毁灭。
渐渐的,小屁孩儿的行为目的性会越来越强。
提示:按此说法,所谓的terrible 2 (可怕的2岁) 就是小屁孩企图用自己的行为开始有目的的来左右这个世界咯,刺探爹妈的底线。
2
前运算阶段(Preoperational Stage):2-7岁
在这个阶段的儿童能够感知图像和语言了,但是他们更倾向于直觉而不是逻辑思考。这个阶段的屁孩儿的思考模式基本就是那首歌,“跟着感觉走”(请抓住梦的手~)……
一个著名的例子是,皮亚杰和儿子散步的时候看见一个蜗牛,走着走着又看见一个,他的儿子直接判断这两个蜗牛是同一个。
这个阶段的后期,孩子开始有了直觉思考,他们开始建立一些判断逻辑,尽管这种逻辑错的一塌糊涂。皮亚杰最有名的实验之一就是这个阶段的屁孩儿对物体守恒(conservation)概念的理解。
如果你在屁孩儿面前放两个形状不同的杯子,一个胖矮,一个细高,然后把同样多的液体倒入两个杯子中,问屁孩儿哪个杯子中的水多?他们直指那个细高的。
皮亚杰说,物质守恒没法教,只能通过孩子不断的自己积累经验,不断的去和周围的世界互动中慢慢体会到。
值得注意的是,这个阶段的孩子还不具备反向思维能力, 这个的意思是,孩子还不能反着想问题,回到问题的起点。
敲黑板,两个黑洞分糖果的问题就需要这个思维能力你不觉得么?
3
具体运算阶段(Concrete Operations Stage):7-11岁
这个阶段的小屁孩儿不仅掌握了物体守恒的概念,而且能头头是道的讲给你听为什么A=B。他们的逻辑思考能力开始形成,初步具有了算数的能力 。他们开始可以对同一件东西做出多重分析,比如,苹果既是苹果,也是水果,也可以算是一件东西。同时,他们可以开始换位思考,世界不再仅仅是由他们单一的感受组成的。
4
形式运算阶段(Formal Operational Stage):从12岁及以上
终于,屁孩儿们能够开始理解抽象的事物并且越来越有逻辑了 。这个阶段的另一个重要发展是反身抽象能力, 这对逻辑数学能力的发展至关重要。
比如类比两个事物,提取他们的某种关系并且进行比较。屁孩儿成长为小小少年,开始可以对自己的行为进行思考,提炼并且抽象化。
对号入座,你会发现什么呢?
分糖果的这个题目,要动用反向思维能力 (一年级的小屁孩儿还不见得有哦),以及一定程度上需要反式抽象能力 (提炼出A和B的糖果之间的关系)。这不仅仅是数学和数(3声)数(4声)的能力,更是认知能力的考验。
对于小学一年级还在组装中的CPU来说,运算任务有点重你不觉得么?
这也是为什么,如果一年级的小朋友卡在这个题目上,我基本不会担心是CPU出了问题——这仅仅说明CPU还没到达出厂状态。
把具体数字代入,把步骤帮小朋友重新梳理一下,或是画个图,都可以帮住他们把这个分糖果的过程变得更具体,更容易理解。
必须说明一点:不是所有的孩子都得按照皮亚杰给出的年龄划分组装CPU。
你们送孩子去上那么多的辅导班,也不能都是白上的呀!认知标志年龄的提前是有可能的,但是过早的给孩子超出他们认知阶段的题目,并不见得是好事。还有,有意思的是,很少见到家长因为孩子语文或者英语题做错了就怀疑孩子脑子不聪明的,为啥数学题就会呢?智商和数学题没这么简单直接的关联,我们都放宽心,慢慢来。
孩子喜不喜欢数学,说到底,跟他们的学数学和做数学题的时候的体验密不可分。
最后,考考你,这个题目你打算怎么讲给小屁孩儿?(这同样是个不合时宜的一年级题目。)
商店进了一批电视机,第一天卖掉一半,第二天卖了8台,还剩12台。请问,商店一共进了?台电视机。
参考资料:
1.Piaget, J. (1968). Six psychological studies. New York: Vintage Books.
2.Piaget, J. (2001). Studies in reflecting abstraction (R. L. Campbell, Trans.). New York: Psychology Press.
本文经授权转载自公众号成长合作社
(ID:TrulyJustKids)
果壳
ID:Guokr42
果壳整天都在科普些啥啊!
吓得我二维码都屈光不正了!