数学知识什么时候能派上用场呢?- 《魔鬼数学》

运用数学原则高效解决现实生活问题, 注入数学思维精准做出工作生活决策
数学知识什么时候能派上用场呢?
亚伯拉罕·瓦尔德与失踪的弹孔

图自: https://www.slideshare.net/SatelliteCenter/kill-your-presentationnot-your-audience
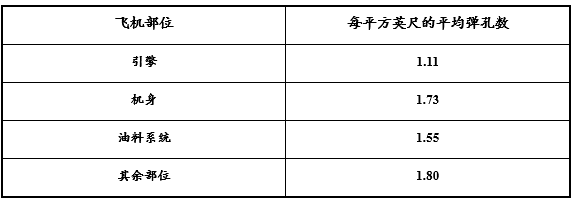
登录查看更多
相关内容
Arxiv
6+阅读 · 2019年8月21日
Arxiv
8+阅读 · 2018年11月21日




