DeepMind高级研究员：重新理解GAN，最新算法、技巧及应用（59页PPT）

---

  新智元推荐  

作者：Balaji Lakshminarayanan

【新智元导读】本文是DeepMind高级研究科学家Balaji Lakshminarayanan在SF AI Meetup上演讲的slides，总结了他以及 Ian Goodfellow，Shakir Mohamed, Mihaela Rosca等人最新的GAN工作。

PPT下载：http://www.gatsby.ucl.ac.uk/~balaji/Understanding-GANs.pdf

《理解生成对抗网络》

包括以下内容：

• GAN与概率机器学习中的其他方法有哪些联系？

• 如何比较分布？

• 生成模型与算法

• 如何结合VAE和GAN来获得更好的结果？

• 缩小理论与实践之间的差距

• 其他一些有趣的研究方向和应用

问题陈述：

一个生成模型

我们的目标是：从真实分布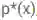给定样本，找到 θ

GAN概述

鉴别器（Discriminator）：训练一个分类器，使用样本区分两个分布

生成器（Generator）：生成愚弄鉴别器的样本

Minimax game：在训练鉴别器和生成器之间交替

• 对应JS散度的最小值的纳什均衡

• 在实践中为了稳定训练需要一些技巧

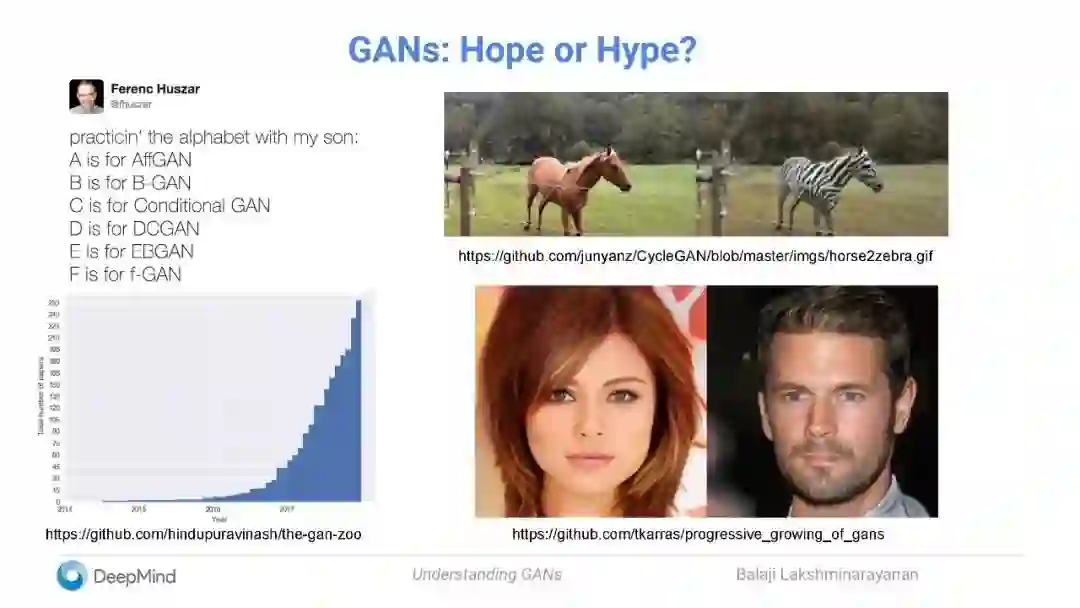
GAN的各种变体非常多

GAN与概率机器学习中的其他方法有哪些联系？

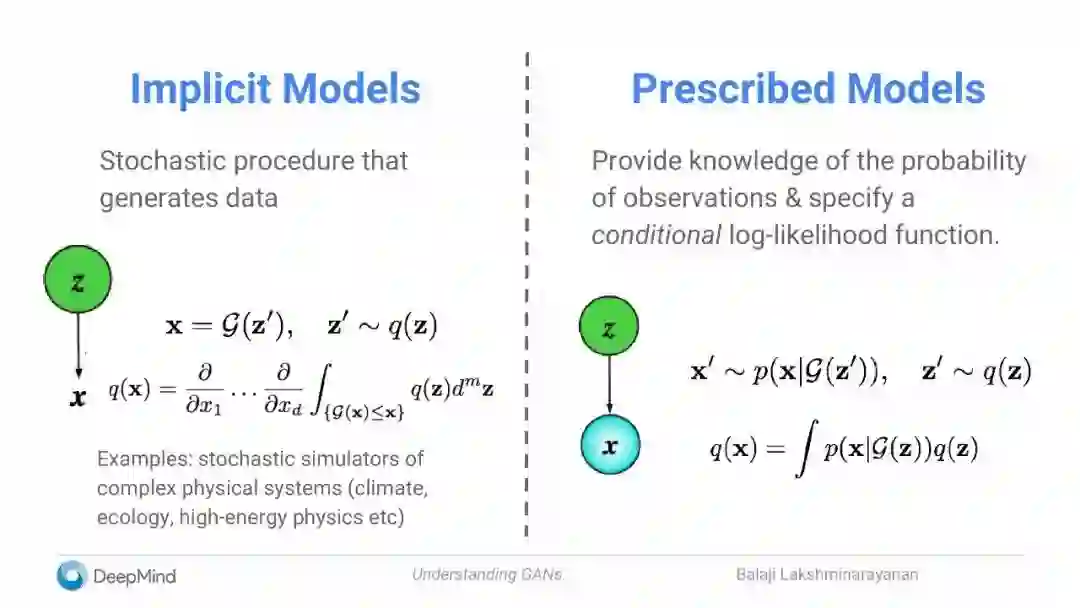
隐式模型：生成数据的随机过程

规定模型：提供有关观察的概率的知识，并指定一个条件对数似然函数。

通过比较学习：使用样本比较估计分布与真实分布

定义一个联合损失函数，并在Comparison loss和Generative loss间交替

如何比较分布？

以下介绍了四种方法，包括：

• 类概率估计

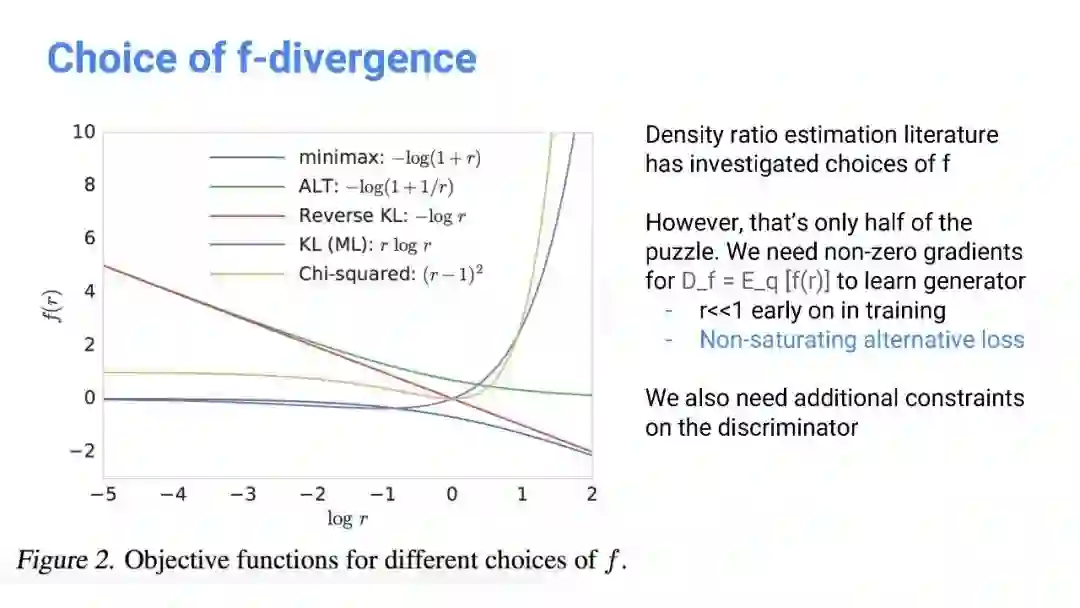
• 散度最小化（f-GAN）

• 密度比估计

• 时矩匹配

如何比较分布？——方法小结

类概率估计 

• 建立一个分类器来区分真实样本和真实样本

• 原始的GAN解决方案

密度比匹配 

• 直接将真实比率与估计值之间的预期误差最小化

散度最小化 

• 最小化真实密度 p* 和乘积 r(x)q(x) 之间的广义散度

• f-GAN方法

时矩匹配（Moment matching）

• 匹配 p* 和 r(x)q(x) 的时矩 

• MMD，最优传输（ optimal transport），等

如何学习生成器？

在GAN中，生成器是可微分的 

• 生成器loss有以下几种形式，例如：f-散度  D_f = E_q [f(r)]

• 可以利用再参数化的技巧

小结：在隐式生成模型中学习

密度比估计 

• 但它们不专注于学习生成器 

近似贝叶斯计算（ABC）和likelihood-free 推理 

• 低维，理论更好理解

• 对参数的贝叶斯推断 

• 模拟器通常是不可微分的

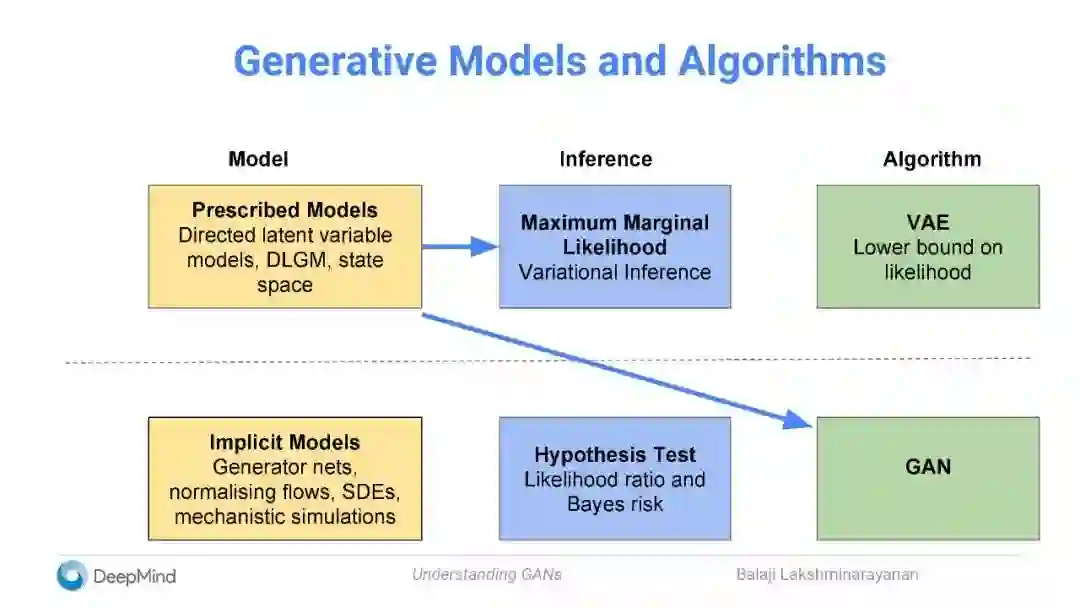
生成模型与算法

对一个固定模型，比较其推理算法

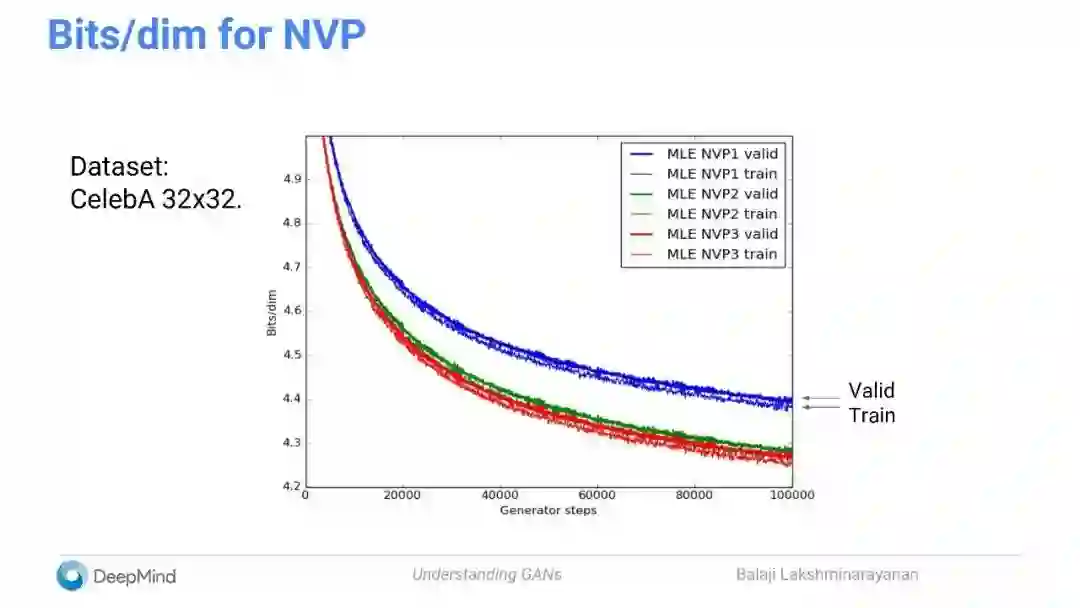
1. 用最大似然估计（MLE）训练 

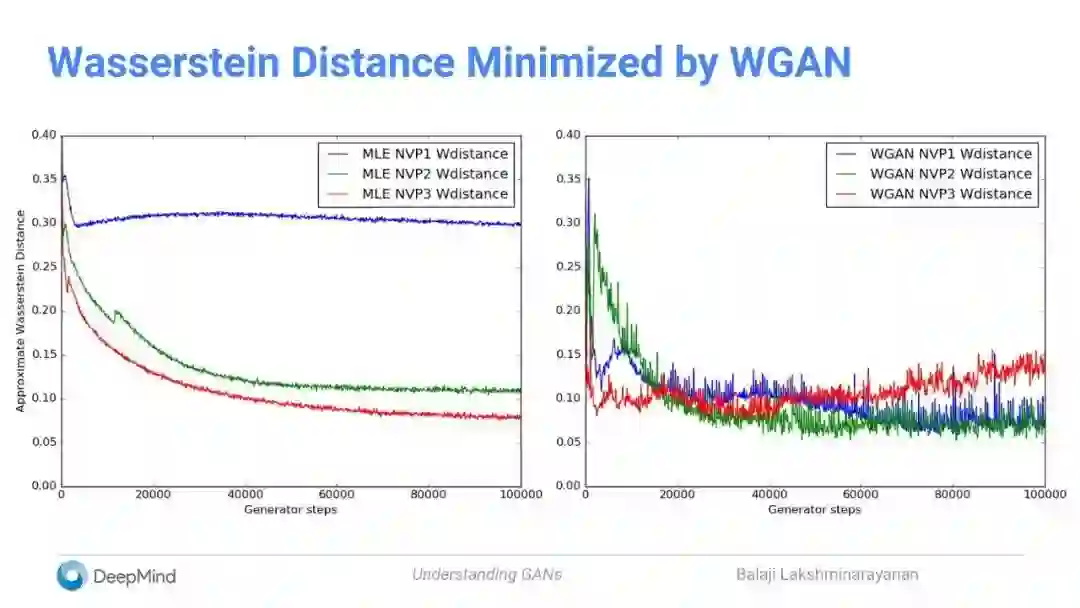
2. 通过Wasserstein GAN训练生成器

3. 比较
   

小结：

• Wasserstein距离可以比较模型。 

• 通过训练critic可以近似估计Wasserstein距离。 

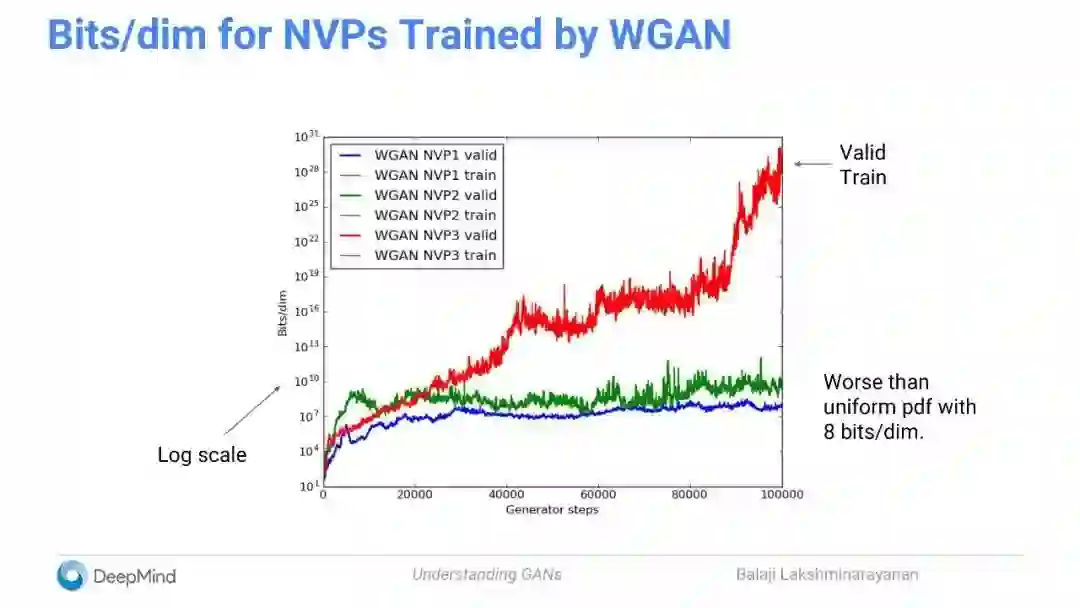
• 通过WGAN进行训练能得到更好的样本，但对数概率显著更差。

• 通过WGAN训练的Latent code是非高斯的。

如何结合VAE和GAN来获得更好的结果？

 Mode collapse问题：

•  “Unrolled GAN”论文中的MoG toy 的例子

• VAE还有其他问题，但不会遭到Mode collapse

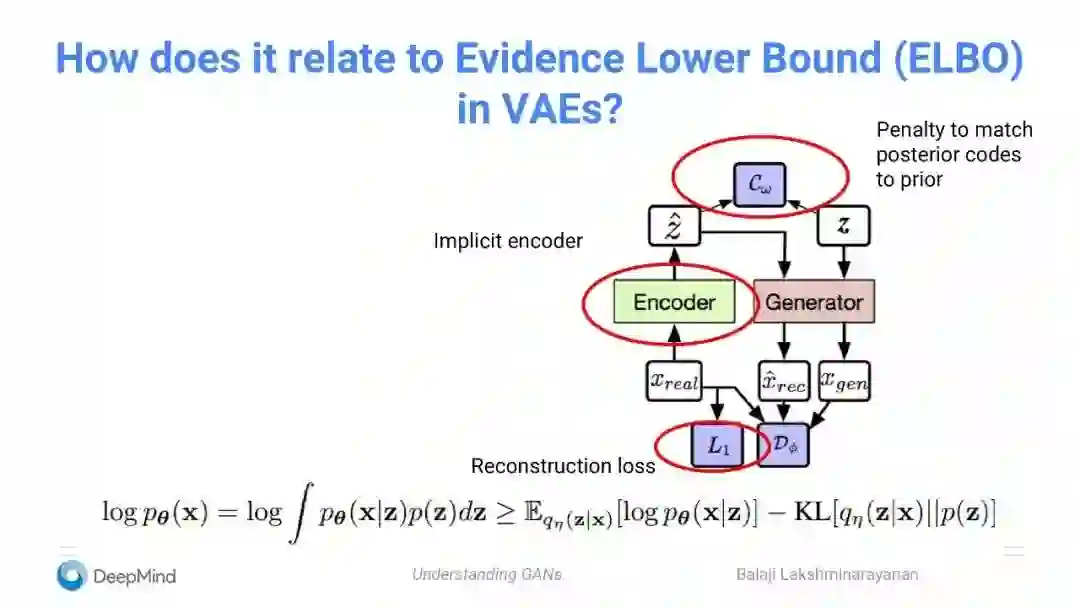
将自动编码器添加到GAN，及与VAE中Evidence Lower Bound (ELOB)的关系

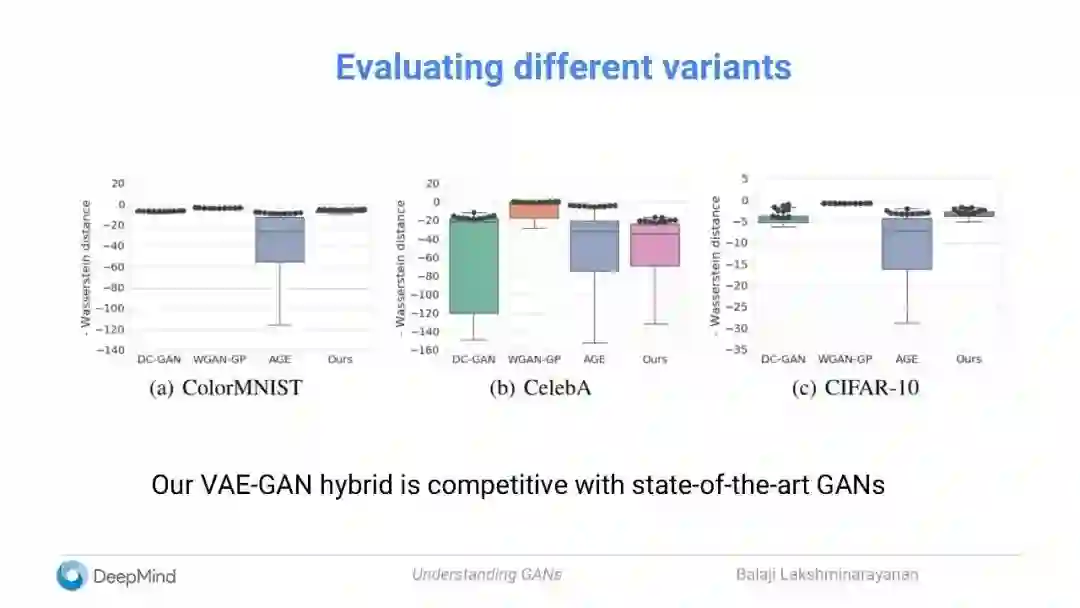
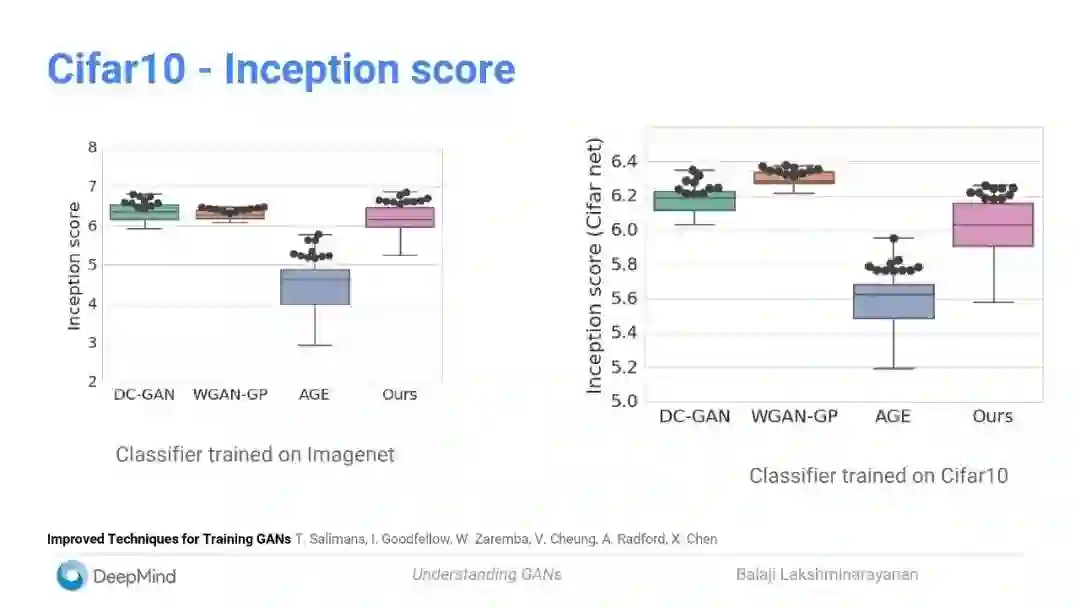
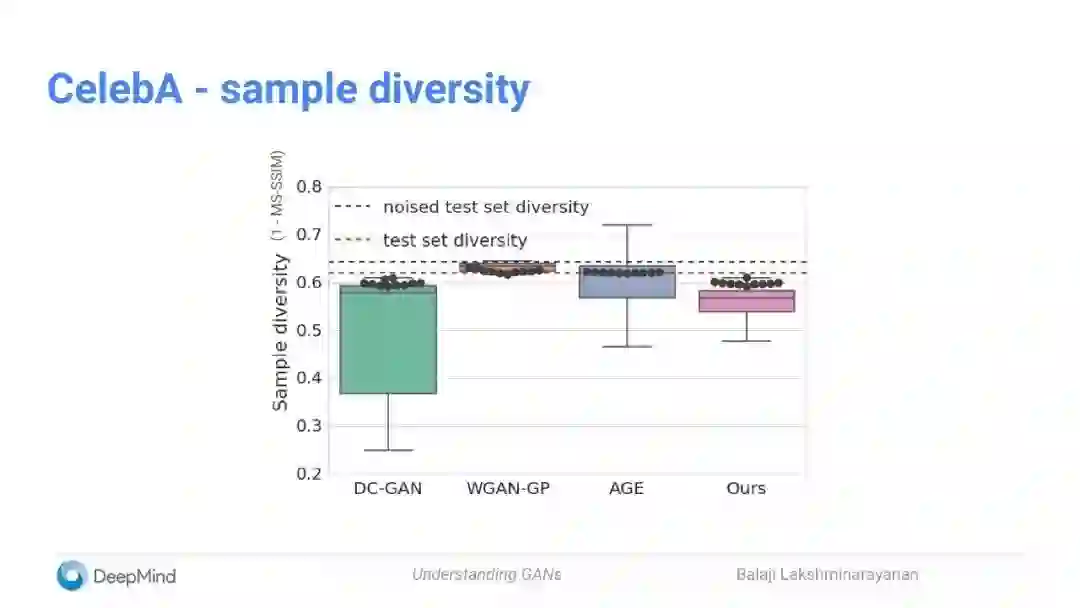
评估不同的变体

我们的VAE-GAN的混合模型可与state-of-the-art的GANs相媲美

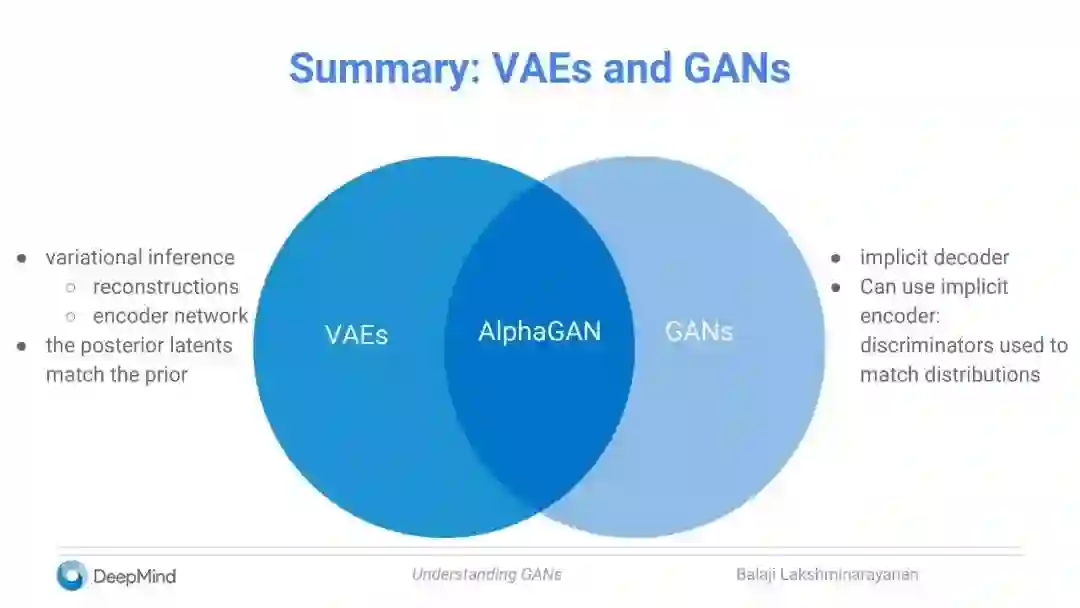
小结：VAEs和GANs

VAE:

• 变分推理：重构；编码器网络

• 后期的latent与先前的匹配

GAN：

• 隐式解码器

• 可以使用隐式编码器：用于匹配分布的鉴别器

缩小理论与实践之间的差距

GAN理论与实践的区别

已经有许多新的GAN变体被提出（例如Wasserstein GAN） 

• 由新理论激发的损失函数和正则化项

• 理论与实践之间的有显着区别

如何弥补这个差距？

• 理论预测失败的综合数据集

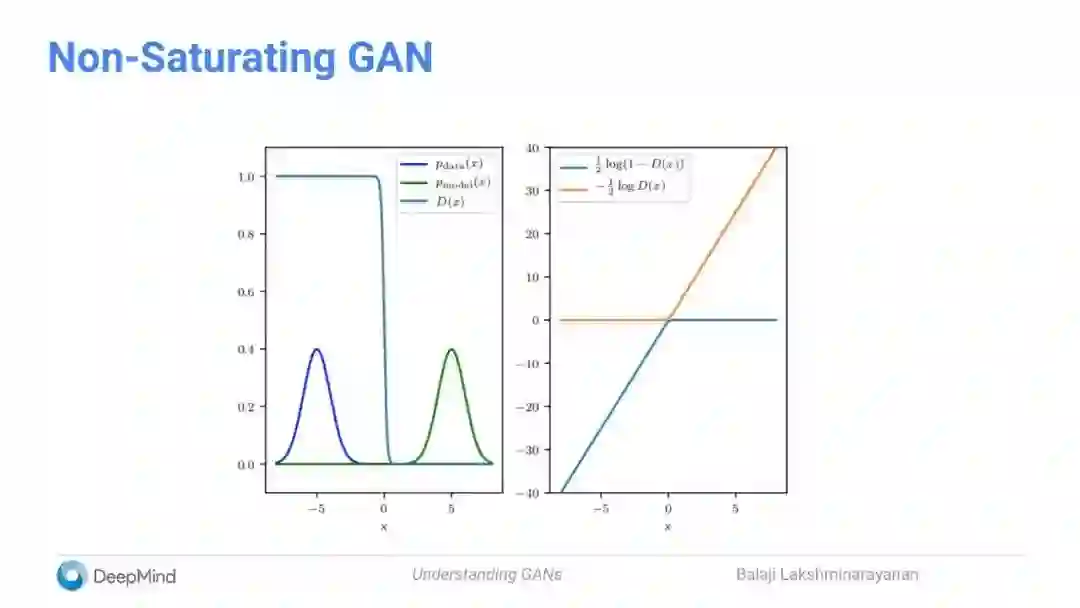
• 将新的正规化项添加到原始non-saturating GAN

Jensen Shannon divergence失败时的合成数据集比较 

• Gradient penalty能得到更好的表现

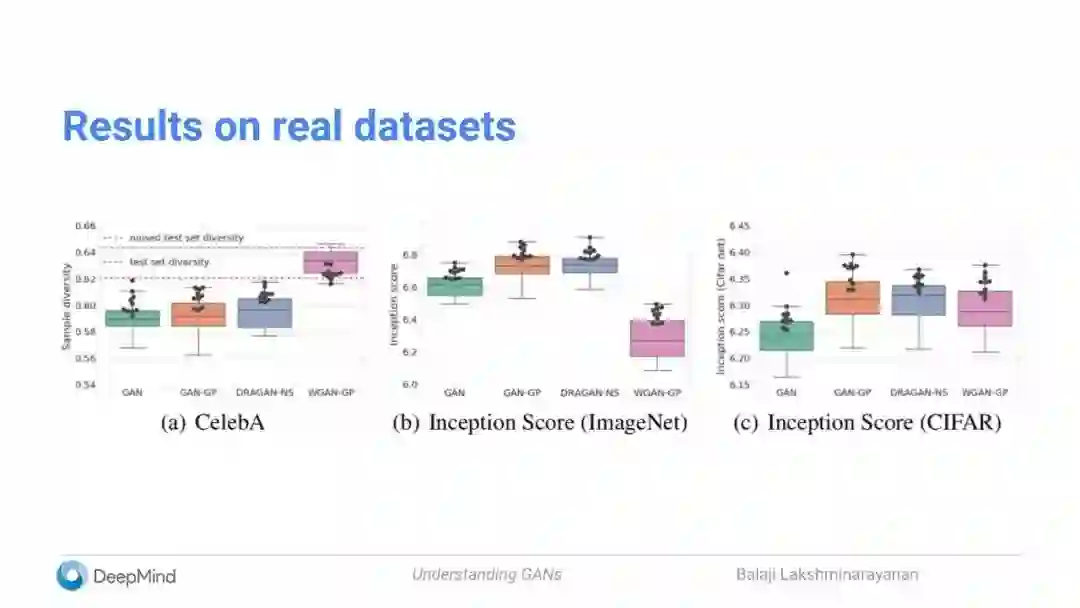
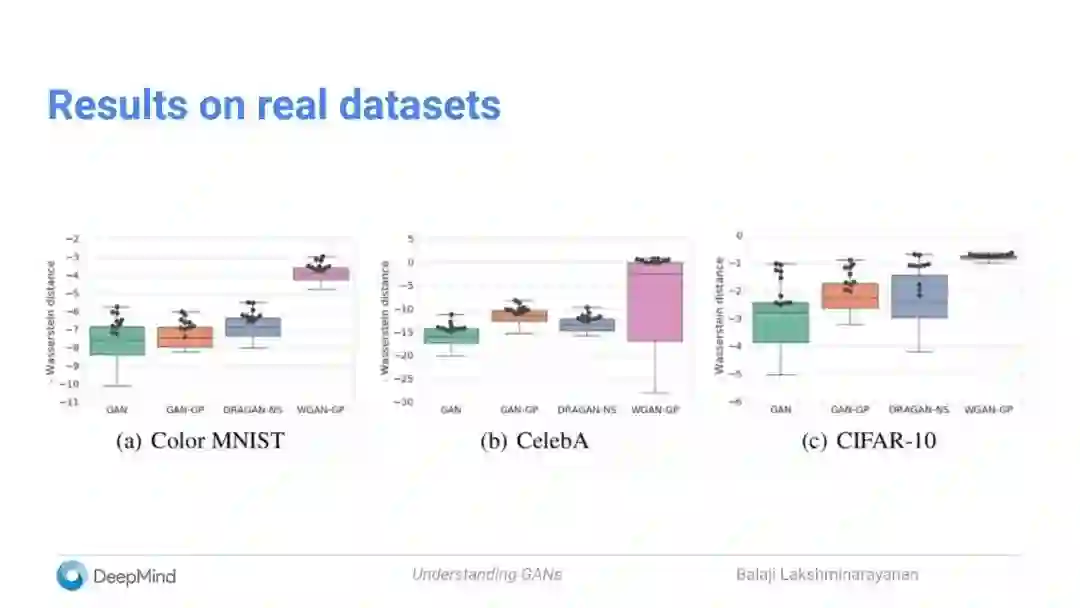
在真实数据集上的结果

小结：

一些令人惊讶的发现： 

• 梯度惩罚（gradient penalty）也能稳定（非Wasserstein的）GAN 

• 不仅要考虑理想的损失函数，还要考虑优化

其他一些有趣的研究方向：

GAN用于模仿学习

• 使用一个单独的网络（鉴别器）来“学习”现实的动作

• 对抗模仿学习：RL奖励来自鉴别器

研究：

• 利用纳什均衡收敛的想法

• 与RL（actor-critic方法）的联系

• 控制理论

应用：

• Class-conditional生成

• 文本-图像生成

• 图像-图像转换

• 单图像超分辨率

• 域适应

小结：

稳定GAN训练的方法 

• 结合自动编码器

• 梯度惩罚

GAN文献中一些有用的工具：

• 密度比（density ratio）的技巧在其他领域也很有用（例如信息传递）

• 隐式变分逼近

• 学习一个现实的损失函数

• 如何处理不可微分的模拟器？——使用可微分近似进行搜索？

---

加入社群

新智元AI技术+产业社群招募中，欢迎对AI技术+产业落地感兴趣的同学，加小助手微信号: aiera2015_1 入群；通过审核后我们将邀请进群，加入社群后务必修改群备注（姓名-公司-职位；专业群审核较严，敬请谅解）。

此外，新智元AI技术+产业领域社群(智能汽车、机器学习、深度学习、神经网络等)正在面向正在从事相关领域的工程师及研究人员进行招募。

加入新智元技术社群 共享AI+开放平台