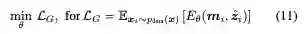DeepMind论文：深度压缩感知，新框架提升GAN性能

---

  新智元报道  

来源：arxiv

编辑：肖琴

【新智元导读】DeepMind提出一种全新的“深度压缩感知”框架，将压缩感知与深度学习相结合，显著提高了信号恢复的性能和速度，并提出一种改进GAN的新方法。

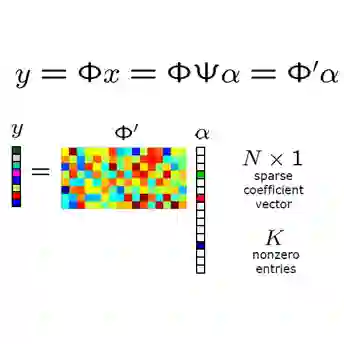
压缩感知(CS)是一种优雅的框架，用于从压缩信号中恢复稀疏信号。

例如，CS可以利用自然图像的结构，仅从少量的随机测量中恢复图像。

CS具有灵活性和数据效率高的优点，但由于其稀疏性和昂贵的重建过程，CS的应用受到限制。

那么，将CS与深度学习的思想相结合，是否能得到更优雅的框架呢？

近日，DeepMind的Yan Wu，Mihaela Rosca，Timothy Lillicrap等研究人员在ICML 2019发表论文Deep Compressed Sensing，基于前人将CS和神经网络生成器结合起来的方法，提出一个全新的框架。

深度压缩感知(DCS)框架通过联合训练生成器和通过元学习优化重建过程，显著提高了信号恢复的性能和速度。作者探索了针对不同目标的测量训练，并给予最小化测量误差推导出一系列模型。

作者表示：“我们证明了，生成对抗网络(GANs)可以被视为这个模型家族中的一个特例。借鉴CS的思想，我们开发了一种使用来自鉴别器的梯度信息来改进GAN的新方法。”

压缩感知，一种优雅的框架

压缩感知是什么呢？

有人这样评价道：

压缩感知是信号处理领域进入 21 世纪以来取得的最耀眼的成果之一，并在磁共振成像、图像处理等领域取得了有效应用。压缩感知理论在其复杂的数学表述背后蕴含着非常精妙的思想。基于一个有想象力的思路，辅以严格的数学证明，压缩感知实现了神奇的效果，突破了信号处理领域的金科玉律 —— 奈奎斯特采样定律。即，在信号采样的过程中，用很少的采样点，实现了和全采样一样的效果。[1]

编码和解码是通信中的核心问题。压缩感知(CS)提供了将编码和解码分离为独立的测量和重建过程的框架。与常用的自动编码模型(具有端到端训练的编码器和解码器对)不同，CS通过在线优化从低维测量重建信号。

该模型架构具有高度的灵活性和采样效率：高维信号可以从少量随机测量数据中重建，几乎不需要或根本不需要任何训练。

CS已经成功地应用于测量噪声大、成本高的场景，如MRI。它的采样效率使得诸如“单像素相机”的开发成为可能，可以从单个光传感器重全分辨率的图像。

然而，尤其是在现代深度学习方法蓬勃发展的大规模数据处理中，CS的广泛应用受到了它的稀疏信号假设和重建优化过程缓慢的阻碍。

最近，Bora et al. (2017)将CS与单独训练的神经网络生成器相结合。虽然这些预训练的神经网络没有针对CS进行优化，但它们表现出的重建性能优于现有的方法，如Lasso (Tibshirani, 1996)。

在本文中，我们提出一种深度压缩感知框架(deep compressed sensing，DCS)，在此框架中，神经网络可以从头开始训练，用于测量和在线重建。

我们证明，深度压缩感知框架可以自然地生成一系列模型，包括GANs，可以通过训练具有不同目标的测量函数推导得出。

这项工作的贡献如下：

• 我们展示了如何在CS框架下训练深度神经网络。

• 结果表明，与以往的模型相比，元学习重建方法具有更高的精度和快几个数量级的速度。

• 我们开发了一种新的基于潜在优化的GAN训练算法，提高了GAN的性能。

• 我们将这个新框架扩展到训练半监督GAN，并表明潜在优化会产生具有语义意义的潜在空间。

深度压缩感知：结合深度神经网络

我们首先展示了将元学习与Bora et al. (2017)的模型相结合的好处。然后将测量矩阵推广到参数化的测量函数，包括深度神经网络。

之前的工作依赖于 random projection作为测量函数，而我们的方法通过将RIP作为训练目标来学习测量函数。然后，我们通过在测量上添加RIP之外的其他特性，得到了两个新的模型，包括一个带有鉴别器引导的潜在优化的GAN模型，这导致了更稳定的训练动态和更好的结果。

压缩感知与元学习

我们假设CSGM(Bora et al. 2017)的运行时效率和性能可以通过使用元学习训练潜在的优化过程、通过梯度下降步骤的反向传播来提高。

CS模型的潜在优化过程可能需要数百个或数千个梯度下降步骤。通过使用元学习来优化这个优化过程，我们的目标是用更少的更新来实现类似的结果。

为此，我们训练模型参数，以及潜在的优化程序，以尽量减低预期的测量误差:

我们的算法如下：

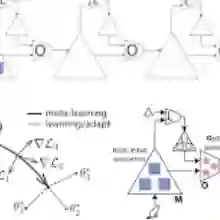
算法1：元学习压缩感知

具有学习测量函数的深度压缩感知

在算法1中，我们使用RIP属性来训练生成器。我们可以使用相同的方法，并加强RIP属性来学习测量函数F本身，而不是使用random projection。

下面的算法2总结了这个扩展算法。我们称之为深度压缩感知(DCS) ，以强调测量和重建可以是深度神经网络。

算法2：深度压缩感知

实验和结果

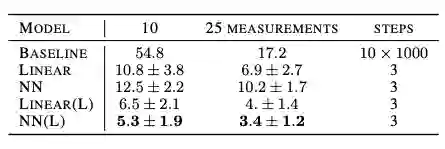
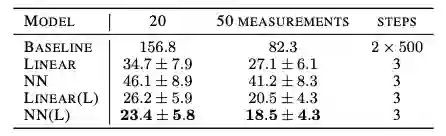
表2和表3总结了我们的模型以及Bora等人的基准模型的结果。

表2：使用不同测量函数的MNIST测试数据的重建损失。除了第一行之外，所有行都来自我们的模型。“±”表示测试样本间的标准差。(L)表示习得的测量函数，越低越好。

表3：使用不同测量函数的CelebA测试数据的重建损失。除了第一行之外，所有行都来自我们的模型。“±”表示测试样本间的标准差。(L)表示习得的测量函数，越低越好。

可以看到，DCS的性能明显优于基准。此外，虽然基线模型使用了数千个梯度下降步骤，并且多次重启，但是我们只使用了3个步骤，没有重启，大幅提高了效率。

有趣的是，对于固定的函数F，随机线性投影的表现优于神经网络。这个实证结果符合压缩感知文献中描述的随机投影的最优性，以及更通用的Johnson-Lindenstrauss定理。

更多结果如下：

表4：与 Spectral Normalised GANs的比较。

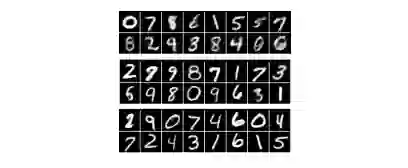
图2：利用随机线性投影(上)、训练线性投影(中)和训练神经网络(下)的10个测量的重建。

图3：使用0(左)、3(中)和5(右)个梯度下降步骤进行潜在优化的CS-GAN样本。采用0步骤的CS-GAN相当于原始GAN。

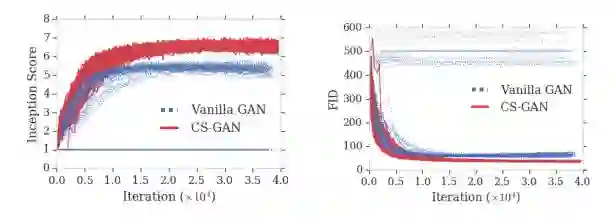
图4：在CIFAR训练期间的Inception Score(越高越好)和FID分数(越低越好)。

论文地址：

https://arxiv.org/pdf/1905.06723.pdf

参考：

[1]形象易懂讲解算法 II—— 压缩感知 

https://zhuanlan.zhihu.com/p/22445302

新智元春季招聘开启，一起弄潮 AI 之巅！

岗位详情请戳：

【加入社群】

新智元 AI 技术 + 产业社群招募中，欢迎对 AI 技术 + 产业落地感兴趣的同学，加小助手微信号：aiera2015_2   入群；通过审核后我们将邀请进群，加入社群后务必修改群备注（姓名 - 公司 - 职位；专业群审核较严，敬请谅解）。